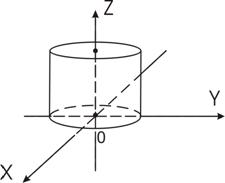
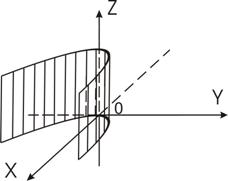
Цилиндрические поверхности

Определение. Цилиндрической поверхностью называется множество параллельных прямых (образующих), проходящих через все точки некоторой линии, называемой направляющей.

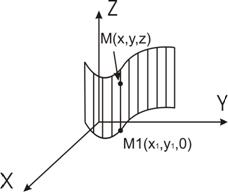
Пусть цилиндрическая поверхность задана таким образом в прямоугольной системе координат OXYZ, что образующие этой

поверхности параллельны оси OZ, а направляющая лежит в плоскости OXY и задается уравнением:

F(x,у) =0

Если взять произвольную точку M(z,y,z) на цилиндрической поверхности, то ее проекция на плоскость OXY есть точка M₁(х₁,у₁,0). Так как точки M и М₁ лежат на образующей, то х₁=х, у₁=у. А так как точка М₁ лежит на направляющей, то координаты точки М₁, а, значит, и точки M, удовлетворяют уравнению F(x,у)=0.

Итак, уравнению удовлетворяют координаты любой точки

цилиндрической поверхности. Следовательно, уравнение

F(x,у)=0

– искомое уравнение цилиндрической поверхности.

Если в прямоугольной системе координат OXYZ направляющая является кривой второго порядка, задаваемой каноническим уравнением вида F(x,у)=0, а образующие параллельны оси OZ, то цилиндрическими поверхностями второго порядка будут:

1) х²+y²=z² — прямой круговой цилиндр;

2) 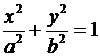- эллиптический цилиндр;

3) - гиперболический цилиндр;

4) у²=2рх - параболический цилиндр.

Заметим, что характерной чертой уравнения рассматриваемых цилиндрических поверхностей, является отсутствие в этих уравнениях одной из переменных.

Не нашли, что искали? Воспользуйтесь поиском: