Ферма, Ролль, Лагранж теоремалары 3 страница

43. Бірінші ретті біртекті сызықты дифференциалдық теңдеулер. Мысалдар

. Егер теңдеу (2’) мынадай түрде y' = жазылатын болса, ол бiртектi дифференциалды теңдеу деп аталады.Бұл теңдеуді шешу үшін деген жаңа айнымалы енгіземіз. Осыдан , дифференциалдап, , (4) теңдеуге қоямыз: . екенін ескеріп теңдеуді мына түрде көшіріп жазсақ: .Айнымалысы ажыратылатын теңдеу аламыз. Теңдеудің екі жағын көбейткішке бөліп айнымалысын ажыратамыз, Біртекті дифференциалды теңдеу біртекті функция ұғымымен байланысты. функциясы k ретті біртекті функция деп аталады, егер кез-келген саны үшін мынадай теңдік орындалса: Мысалы, -екінші ретті біртекті функция, себебі 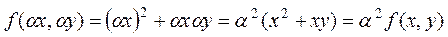.Ал - нолінші ретті біртекті функция, себебі дифференциалды теңдеудегі функция нолінші ретті біртекті функция болса, онда теңдеу (4) біртекті түрге келтіріледі. Мысалы, теңдеуді шешу керек. Шешуі. 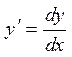екенін ескеріп теңдеуді мына түрде жазайық: . Сонда - нолінші ретті біртекті функция болғандықтан ол біртекті түрге келеді: Шешу үшін деген жаңа айнымалы енгізіп, осыдан , дифференциалдап, , теңдеуге қоямыз: . екенін ескеріп теңдеуді мына түрде көшіріп жазсақ: . Айнымалысы ажыратылатын теңдеу аламыз. Теңдеудің екі жағын көбейткішке бөліп айнымалысын ажыратамыз, Мүшелеп интегралдасақ, , осыдан . Енді белгілеуді орнына қойсақ екендігі шығады. Алынған шешім болып тұрған функция айқын емес түрде алынды. Кейде оны дифференциалды теңдеудің жалпы интегралы деп те атайды

44. Бірінші ретті сызықты дифференциалдық теңдеулер. Мысалдар.

Бiрiншi реттi дифференциалды теңдеу сызықты деп аталады, егер ол мынадай түрде жазылатын болса: y'+P(x)y=Q(x) Егер (5) теңдеудегі Q(x)=0 болса сызықты теңдеу біртекті деп аталады y'+P(x)y=0. Сызықты біртекті дифференциалды теңдеу шешімін айнымалыны алмастыру әдісімен бірден алуға болады: Сонымен, сызықты бiртектi дифференциалды теңдеудiң жалпы шешiмi мынадай: .Енді (5) теңдеуді шешумен айналысайық. Лагранж әдісі: Бұл әдіс (5) теңдеу шешімін сәйкес біртекті теңдеуінің шешімінен алады. Біртекті теңдеуінің шешіміндегі С шаманы х -тен тәуелді функция деп қарастырамыз С(х) функциясын табу үшін у және 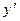мәндерін (5) теңдеуге қоямыз. 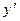тауып алайық: ; екенін ескеріп, мынаны аламыз: .Мүшелеп интегралдап, белгісіз С(х) функцияны табамыз: С(х) функция мәнін (*) теңдеуге қойып сызықты дифференциалды теңдеу шешімін аламыз: Мысал. дифференциалды теңдеуді шешу керек. Шешуі. Теңдеудің екі жағын х- ке бөлсек, сызықты теңдеу аламыз: , мұнда P(x)= , Q(x)=2x³ . Теңдеудің шешімін табу үшін (7) формуланы қолданамыз. Сонымен, берілген сызықты теңдеу шешімі: .

46. Ықтималдықтың классикалық және статистикалық анықтамасы

Анықтама. Сынақ нәтижесінде орындалуы да орындалмауыда мүмкін болатын оқиғаны кездейсоқ оқиға дейміз. Кездейсоқ оқиғаларды латын алфавитінің А, В, С бас әріптерімен белгілейді А-ма. Сынақ нәтижесінде міндетті түрде болатын оқиға ақиқат оқиға деп, ал сынақ нәтижесінде ешқашан орын­далмайтын оқиға жалған оқиға д а. Әдетте ақиқат оқиғаны U, ал жалған оқиғаны V әріптерімен белгілеу қабылданған. А-ма. Кездейсоқ оқиғалардың бiреуiнiң пайда болуы басқасының пайда болуын жоққа шығарса олар өзара үйлесiмсiз деп аталады. Ал оқиғалардың бiреуiнiң пайда болуы басқасының пайда болуына әсер етпесе олар өзара үйлесiмдi деп аталады. Тәжірибе нәтижесінде пайда болатын барлық мүмкін оқиғалар элементар оқиғалар жиынын құрайды. Элементар оқиғалар қос-қостан үйлесімсіз болса, олар оқиғалардың толық тобын құрайды дейді. А-ма. Тәжірибедегі ізделінді оқиғаның пайда болуына қолайлы жағдайларсанының, барлық элементар оқиғалар санына қатынасы оқиға ықтималдығы деп аталады және Р әрпімен белгілейді: мұндағы А – ізделінді оқиға, т - осы оқиғаның пайда болуына қолайлы жағдайлар саны, п - элементар оқиғалар саны. Осы анықтаманы ықтималдықтың классикалық анықтамасы деп атайды.Ы-тың классикалық анықтамасынан мынадай қасиеттер шығады:1. Ақиқат оқиға ықтималдығы бірге тең: .Шынында да, ақиқат оқиға үшін m=n. Онда . 2. Жалған оқиға ықтималдығы бірге тең: . Шынында да, ақиқат оқиға үшін m =0. Онда . 3. Кездейсоқ оқиға ықтималдығы ноль мен бірдің арасында жататын нақты сан болад .Шынында да, кездейсоқ оқиға үшін 0<m<n. Теңсіздіктің екі жағын n-ге бөліпсек, аламыз, олай болса: .Осы үш қасиеттен кез келген оқиға үшін мына теңсіздік орындалатыны шығады: 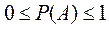. Ы-тың классикалық анықтамасы оқиғалар саны шексіз болғанда қолданылмай қалады. Кейде оқиғалардың толық топ құратынын анықтау қиынға соғады. Сондай жағдайларда ықтималдықтың стаатистикалық анықтамасын қолданады. Тәуелсіз п рет тәжірибе жасадық дейік. Әр жолы ізделінді А оқиғаның пайда болу ықтималдығы тұрақты болсын. Тәжірибе нәтижесінде А оқиғасы т рет пайда болды дейік А-ма. Тәжірибе нәтижесінде А оқиғасы пайда болған оқиғалар санының барлық тәжірибелер санына қатынасы оқиғаның салыстырмалы жиілігі деп аталады , мұндағы m - А оқиғасы пайда болған тәжірибелер саны, ал n - барлық тәжірибелер саны. Тәжрибелер саны артқан сайын оқиғаның салыстырмалы жиілігі қандай да бір тұрақты сан маңайына шоғырманған. Бұл заңдылық статистикалық тұрақтылық делінеді. Статистикалық тұрақтылыққа көз жеткізу үшін Ж.Бюффон және К.Пирсон деген ғалымдар теңгені көп рет лақтырып тәжірибе жасаған. Тәжірибе нәтижесі кестеде келтірілген:

Тәжірибелер саны артқан сайын елтаңба түсу саны 0,5 санына жақындайды екен. Ал елтаңбаның түсу ықтималдығы . Олай болса, салыстырмалы жиілік оқиға ықтималдығына жақындайды екен А-ма. Статистикалық тұрақтылық пайда болған кездегі салыстырмалы жиілік оқиға ықтималдығы деп қабылданады . Бұл анықтаманы ықтималдықтың статистикалық анықтамасы деп атайды.

47. Комбинаторика элементтері

Өмірде қарапайым бір әрекеттен ғана тұратын оқиғалар аз кездеседі. Көбіне бір оқиға орындалуының әртүрлі әдістері бар болады немесе қарастыры отырған оқиғаны бірнеше кезеңдерге бөліп орындау керек болады. Осындай оқиға­лардың жалпы және қолайлы жағдайлар санын есептеуге мүмкіндік беретін қосу және көбейту ережелерін білуіміз қажет.

Қосу ережесі. Қандай да бір оқиға орындалуының бірнеше m₁, m₂,..., m_k

Түрлі тәсілдері болса сол оқиғаны орындаудың барлығы m₁+m₂+...+m_k

түрлі тәсілі бар болады.

Көбейту ережесі. k кезеңнен тұратын қандай да бір оқиғаны іске асыру керек болсын. Бірінші кезеңді орындаудың m_1, екінші кезеңді орындаудың m₂ т.с.с. k кезеңді орындаудың m_k тәсілі бар болса сол оқиғаны толық іске асырудың барлығы m₁×m₂×...×m_k

түрлі тәсілі болады.

Алмастырулар. п элементтен тұратын және бір-бірінен тек орналасу ретімен ғана өзгешеленетін комбинацияларды п элементтен жасалған алмастырулар деп атайды. Элементтен жасалған алмастырулар санын Р_n деп белгілейді және алмастырулар санын есептеу үшін мынадай формула қолданады:

Р_n=n! (1)Мұндағы n!=1×2×3×...×n.

Орналастырулар. N элементтің m элементінен тұратын (m<n) және бір-бірінен құрамы немесе орналасу реті бойынша өзгешеленетін комбинациялар n элементтен m элемент бойынша жасалған орналас­тырулар  деп аталады.

n элементтен m элемент бойынша жасалған орналастыру санын деп белгілейді және оны есептеу үшін мына формула қолданылады: (2)

Терулер. N элементтің m элементі­нен тұратын (m<n) және бір-бірінен құрамы бойынша ғана өзгешеленетін комбинация­лар n элементтен m элемент бойынша жасалған теру  деп аталады.

n элементтен m элемент бойынша жасал­ған теру саны деп белгіленеді және оны табу үшін мына формула қолданылады: (3)

48. Ықтималдықтардың қосу және көбейту теоремалары.

m₁+m₂+...+m_k Көбейту ережесі m₁×m₂×...×m_k. Алмастырулар. Р_n=n! Орналастырулар Терулер. Ықтималдықтарды қосу және көбейту. А мен В оқиғаларының кемінде біреуі орындалғанда пайда болатын оқиғаны осы оқиғалардың қосындысы деп атайды және А+В деп белгілейді. А мен В оқиғалары қатар пайда болғанда орындалатын оқиғаны осы оқиғалардың көбейтіндісі деп атайды және АВ деп белгілейді.

Теорема. Үйлесімсіз екі оқиға қосындысының ықтималдығы осы оқиғалардың ықтималдықтарының қосындысына тең болады: . Бұл теорема оқиғалар саны екіден көп болғанда да дұрыс болады: егер А₁, А₂,..., А_n оқиғалар қос-қостан үйлесімсіз болса, онда Егер А₁, А₂,..., А_n оқиғалар қос-қостан үйлесімсіз және оқиғалардың толық тобын құраса, онда . А-ма. Тәжірибе нәтижесінде мүмкін болатын екі оқиғаның бірінің пайда болуы екіншісін болдырмаса, ол оқиғалар қарама-қарсы оқиғалар деп аталады. А оқиғасына қарама-қарсы оқиғаны деп белгілейді.

Қарама қарсы оқиғалардың ықтималдықтарының қосындысы бірге тең: . А-ма. Екі оқиғаның бiреуiнiң пайда болуы екiншiсiнiң пайда болу ықтималдығын өзгертпесе олар тәуелсiз деп аталады. Ал екі оқиғаның бiреуiнiң пайда болуы екiншiсiнiң пайда болу. ықтималдығын өзгертсе, олар тәуелдi деп аталады. Теорема Тәуелсіз А мен В оқиғаларының көбейтіндісінің ықтималдығы әр оқиға ықтималдықтарының көбейтіндісіне тең: . Бұл теорема оқиғалар саны екіден көп болғанда да дұрыс болады: егер А₁, А₂,..., А_n оқиғалар қос-қостан тәуелсіз болса, онда .

49. Шартты ықтималдық. Тәуелді оқиғалар

В оқиғасының ықтималдығы А оқиғасының болған болмағанына тәуелді болатын жағдайлар болады.Сондықтан деп, шартты ықтималдық, А оқиғасы орындалып кетті деп есептегендегі В оқиғасының ықтималдығын белгілейді. Мысал. 36 картаның ішінен кез келген 2 карта алынсын. Осы екі картаның бірдей түсті болуының ықтималдығын табу керек. Шешуі. Алдымен алынған екі қартаның бірдей түске(масть) жататынын (айталық қарға) жату ықтималдығын анықтайық. Белгілеу енгізейік: А – алынған бірінші карта қарға; В – алынған екінші карта қарға. В оқиғасының ықтималдығы А оқиғасының пайда болу болмауына байланысты өзгеріп отырады. Сонымен, , . Осыдан Енді , , , алынған екі карта сәйкес төрт түстің біріне жататындығын көрсететін өзара үйлесімсіз оқиғалар болсын. Сонда алынған екі картаның бірдей түсті (С оқиғасы) болуы , , , оқиғалардың кез келгені орындалса пайда болады, яғни,

С = + + + .Олай болса P(С) =P( + + + )=P()+P()+P()+P()= Теорема. Үйлесімді екі оқиға қосындысының ықтималдығы осы оқиғалардың ықтималдықтарының қосындысынан екі оқиғаның қатар пайда болу ықтималдығын алғанға тең болады:.

51. Тәуелсіз сынақтар үшін Бернулли формуласы. Пуассон формуласы. Тәуелсіз п рет тәжірибе жасадық дейік. Әр жолы ізделінді А оқиғаның пайда болу ықтималдығы тұрақты 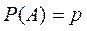болсын. Онда А оқиғасының пайда болмауы болады. Енді осы тәжірибелер нәтижесінде А оқиғасы k рет пайда болу ықтималдығын деп белгілейді және ол мынаған тең: Бернулли формуласы деп атайды.Егер тәжірибелер саны көп болып (п ), ондағы А оқиғасының пайда болу ықтималдығы (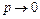) аз болса, ықтималдықты Пуассон формуласымен есептеу қолайлы: 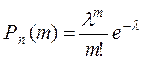мұндағы, , және деп есептейміз. Пуассон формуласын көбінесе деп жазады. Муавр-Лапластың локальді теоремасы. Тәуелсіз п рет тәжірибе жасағанда ізделінді А оқиғаның пайда болу ықтималдығы тұрақты 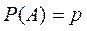болсын. Онда А оқиғасының k рет пайда болу ықтималдығы жуық шамамен мынаған тең: , мұндағы, және п артқан сайын Муавр-Лаплас формуласының мәні дәлірек болады және бұл формуланы болған кезде қолданған жөн. Есептеуді оңайлату үшін ықтималдықтар теориясы оқулықтарында функциясының кестесі беріледі. Бұл функция жұп, яғни f(-x)=f(x), және х артқан сайын функция нолге ұмтылады (х>4 болған кезден бастап оны нолге тең функция деп есептей беруге болады). Муавр-Лапластың интегралдық теоремасы. Тәуелсіз п рет тәжірибе жасағанда ізделінді А оқиғаның пайда болу ықтималдығы тұрақты 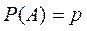болсын. Онда А оқиғасының пайда болу саны 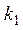мен арасында болу ықтималдығы жуық шамамен мынаған тең: , мұндағы, және , 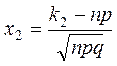п артқан сайын Муавр-Лаплас формуласының мәні дәлірек болады және бұл формуланы болған кезде қолданған жөн. Есептеуді оңайлату үшін ықтималдықтар теориясы оқулықтарында функциясының кестесі беріледі. Бұл функция тақ, яғни f(-x)=-f(x), және х артқан сайын функция бірге ұмтылады (х>4 болған кезден бастап оны 1 тең функция деп есептей беруге болады.

Не нашли, что искали? Воспользуйтесь поиском: