
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Сложные учетные ставки
Рассмотрим теперь антисипативный способ начисления слож-
ных процентов.
Пусть
dc (%) — сложная годовая учетная ставка;
dc — относительная величина сложной учетной ставки;
Icn у — коэффициент наращения для случая учетной ставки;
/ — номинальная годовая учетная ставка.
Тогда по прошествии первого года наращенная сумма S1 в со-
ответствии с формулой (2.5) составит
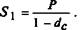
Еще через год эта формула 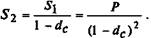 будет применяться уже к сумме S1:
будет применяться уже к сумме S1:
и т. д., аналогично случаю сложных ставок ссудных процентов.
По прошествии п лет наращенная сумма составит
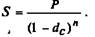 (4.1)
(4.1)
Отсюда для множителя наращения имеем
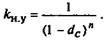 (4.2)
(4.2)
Сравнивая формулы (3.1) и (4.1), легко видеть, что при равен-
стве ссудного процента и учетной ставки наращение первона-
чальной суммы во втором случае (антисипативный метод) идет
быстрее.
Поэтому в литературе часто можно встретить утверждение, что
декурсивный метод начисления более выгоден для заемщика, а
антисипативный — для кредитора. Это можно считать справедли-
вым лишь для небольших процентных ставок, когда расхождение
не столь значительно (рис. 2). Но с ростом процентной ставки
разница в величине наращенной суммы становится огромной
(при этом она сама растет с ростом л), и сравнение двух методов с
точки зрения выгодности утрачивает смысл. Представить себе эту
разницу можно с помощью графика на рис. 3.
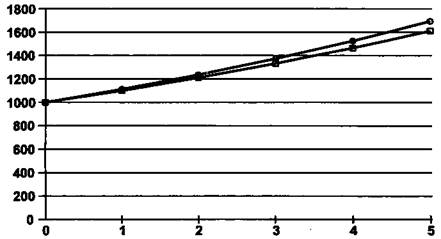
|
Рис. 2. Декурсивный (нижняя кривая) и антисипативный
(верхняя кривая) способы начисления сложных процентов
при *<%) = </<<%) = 10%
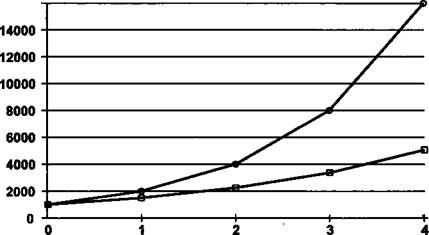
Рис. 2. Декурсивный (нижняя кривая) и антисипативный
(верхняя кривая) способы начисления сложных процентов
при 4<%) = </,<%) = 30%
Из формулы (4.1) также явствует, что для периодов начисле-
ния, превышающих один год, учетная ставка может принимать
значения только строго меньшие (т. е. не достигающие) 100%.
Иначе величины P или S не будут иметь смысла, становясь беско-
нечными или даже отрицательными. Наращенная сумма S очень
быстро увеличивается с ростом d, стремясь к бесконечности, ко-
гда d{%) приближается к 100%.
В следующем разделе рассмотрим, какие учетные ставки дают
результаты, одинаковые с наиболее распространенными в насто-
ящее время ставками ссудных процентов.
Так же, как и при декурсивном способе, возможны различные
варианты начисления антисипативных процентов (начисление за
короткий — меньше года — интервал, начисление т раз в году и
т. д.). Им будут соответствовать формулы, полученные аналогич-
ным образом.
Так, для периода начисления, не являющегося целым числом,
имеем
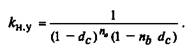 (4.3)
(4.3)
При учетной ставке, изменяющейся в течение срока ссуды, на-
ращенная сумма превращается в
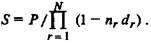 (4.4)
(4.4)
Здесь /I1, /I2,..., nN— продолжительность интервалов начисле-
ния в годах, d{, d2,..., dN — учетные ставки, соответствующие
данным интервалам.
Для начисления процентов т раз в году формула имеет такой
вид:
(4.5)
или
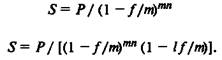 (4.6)
(4.6)
При этом тп — целое число интервалов начисления за весь пе-
риод начисления, / — часть интервала начисления.
При непрерывном начислении процентов S рассчитывается по
формуле:
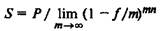 (4.7)
(4.7)
Из полученных формул путем преобразований получаем фор-
мулы для нахождения первоначальной суммы, срока начисления
и величины учетной ставки:
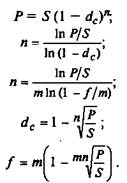
|
(4.8)
(4.9)
(4.10)
(4.11)
(4.12)
Мы рассмотрели различные способы начисления процентов. В
заключение составим таблицу, дающую возможность наглядного
представления результатов, получаемых при этих способах для
одной и той же первоначальной суммы, одинаковых по величине
процентных ставок и периодов начисления п.
Таблица 1. Величина наращенной суммы в зависимости
от вида процентной ставки
P = 10 000 ам. долл., величина процентной ставки — 10%
| Величина нара- щенной суммы | л=1 | л = 3 | л=6 |
| Is=P(I + in) | 13 000 | 16 000 I | |
| \S= P(I + i)" | 13 310 | 17 716 | |
| \S= Pe>" | 13 499 | 18 222 | |
| \S= P/(\-dri) | 11 111 | 14 286 | 25 000 |
| \S= P/(\ -d)" | 11 111 | 13 717 | 18 816 I |
Результаты вычислений, вероятно, будут неожиданными для
большинства читателей — наибольший рост капитала мы имели
бы в случае начисления процентов по простой учетной ставке.
(Следует заметить, что на практике она не применяется на дли-
тельных, больше года, периодах начисления.)
Однако, для того, чтобы выбрать в каждом конкретном случае
наиболее выгодную процентную ставку, не обязательно считать
получаемые суммы. Можно воспользоваться эквивалентными про-
центными ставками, о которых пойдет речь в следующем разделе.
Пример 15
Первоначальная сумма долга равняется 25 000 000 руб. Опреде-
лить величину наращенной суммы через три года при примене-
нии декурсивного и антисипативного способов начисления про-
центов. Годовая ставка — 25%.
Решение
По формулам (3.1) и (4.1) получаем:
51 = 25 000 000 (1 + 0,25)3 = 48 828 125 (руб.);
52 = 25 000 000/(1 - 0,25)3 = 59 255 747 (руб.).
Данный пример наглядно демонстрирует ощутимость различия
в результатах при разных способах начисления процентов. Разни-
ца составляет больше 10 млн. руб.
Пример 16
Определить современное значение суммы в 120 000 000 руб.,
которая будет выплачена через два года, при использовании
сложной учетной ставки 20% годовых.
Решение
Производим расчет по формуле (4.8):
P = 120 000 000 (1 - 0,2)2 = 76 800 000 (руб.).
2.5. Эквивалентность процентных ставок
различного типа
Часто при расчетах, проводимых по различным финансовым
операциям, возникает необходимость в определении эквивалент-
ных процентных ставок.
Эквивалентные процентные ставки — это такие процентные
ставки разного вида, применение которых при одинаковых на-
чальных условиях дает одинаковые финансовые результаты.
Эквивалентные процентные ставки необходимо знать в случа-
ях, когда существует возможность выбора условий финансовой
оперции и требуется инструмент для корректного сравнения раз-
личных процентных ставок.
Для нахождения эквивалентных процентных ставок использу-
ют уравнения эквивалентности, принцип составления которых за-
ключается в следующем. Выбирается величина, которую можно
рассчитать при использовании различных процентных ставок
(обычно это наращенная сумма S). На основе равенства двух вы-
ражений для данной величины и составляется уравнение эквива-
лентности, из которого путем соответствующих преобразований
получается соотношение, выражающее зависимость между про-
центными ставками различного вида.
Вспомним обозначения, использованные ранее:
I — простая годовая ставка ссудного процента;
d — простая годовая учетная ставка;
/с — сложная годовая ставка ссудного процента;
dc — сложная годовая учетная ставка;
j — номинальная ставка ссудного процента;
/ — номинальная учетная ставка.
Повторим формулы для определения наращенной суммы при
различных способах начисления процентов, полученные в пре-
дыдущих параграфах этой главы:
(1.7)
(2.5)
(3.1)
(3.6)
(4.1)
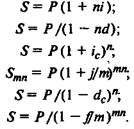 (4.5)
(4.5)
Приравнивая эти формулы попарно, можно получить соотно-
шения, выражающие зависимость между любыми двумя различ-
ными процентными ставками.
Не нашли, что искали? Воспользуйтесь поиском: