СЛУЧАЙ ПОЧТИ РАВНЫХ КОРНЕЙ

Мы уже указывали, что при решении уравнений методом Ньютона — Рафсона могут возникнуть трудности в том случае, если уравнения (5.1) или (5.2) имеют пары близко расположенных корней. В этом случае условие 3 сходимости метода нарушается вблизи такой пары корней. Соответствующая ситуация проиллюстрирована на рис. 5.8 (масштаб сильно увеличен). Заметим, что производная f'(х) близка к 1 при х, равном обоим значениям корней, а₁ и а₂. Более того, на основании теоремы о среднем значении, можно утверждать, что f'(х) равна 1 где-то между а₁ и а₂.

Рис. 5.8. Геометрическое представление того случая, когда с помощью метода Ньютона — Рафсона нельзя определить значение корня (f'(х) близка к 1).

Рассмотрим, что случится, если принять х₀ в качестве исходного значения для корня а₁. Касательная, проведенная через точку С, пересечет прямую у = х в точке А, и следующее приближение будет равно х₁. Касательная, проведенная через точку В, пересекает прямую у = х в точке О, и в качестве следующего приближения снова получается х₀. Итерационный процесс, таким образом, осциллирует между х₀ и х₁ до бесконечности, не сходясь ни к одному значению корня. Другими словами, не удается отделить эти два корня, потому что они расположены слишком близко один к другому. Конечно, мы вправе сказать в этом случае, что нарушено условие 1 сходимости метода и что начальное значение х₀ было недостаточно близко к а ₁.

Это утверждение совершенно верно. Поэтому мы попытаемся разработать метод, с помощью которого можно было бы найти начальное приближение, достаточно близкое к искомому значению корня. Трудности возникают потому, что вычисление знаменателя в формуле (5.14) включает в себя вычитание двух почти равных чисел, а мы уже неоднократно убеждались, что такое вычитание приводит к снижению точности.

Натаниель Мейкон¹) предложил метод, согласно которому сначала находится значение х, при котором f'(х) = 1, т. е. решается уравнение

Пусть решением этого уравнения будет некоторое 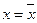. Эта точка расположена между двумя корнями, а ₁ и а ₂. Чтобы получить начальное приближение для решения уравнения, предположим, что 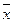лежит посредине между а₁ и а ₂. (Этот случай изображен на рис. 5.9.) Другими словами, мы предполагаем, что 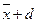и 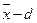являются корнями уравнения (5.2). Разлагая f(x) в ряд Тейлора в окрестности точки 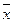и замечая, что 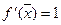, получаем

.

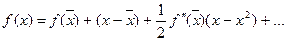Как показано, мы ограничиваем ряд тремя членами. Подставляя 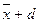вместо х имеем

.

Но по условию

,

поэтому, решая эти уравнения относительно d, получаем

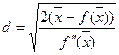
Не воспроизводя выкладки, скажем также, что если уравнение задано в форме (5.1)

F(х) = 0,

то для d. получаем

,

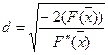так как приходится решать уравнение F'(х) = 0. Рассматривая рис. 5.8, читатель может легко убедиться в том, что величина под корнем положительна.

Рис. 5.9. Геометрическое представление усовершенствованного метода Ньютона — Рафсона для f'(x), близкой к 1.

Процесс решения уравнения сводится теперь к следующему. Если дано уравнение с двумя почти равными корнями, то, определив приблизительно местонахождение этих корней, необходимо решить уравнение

и определить значение 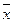. Для решения этого уравнения можно использовать любой подходящий метод, например метод Ньютона — Рафсона. Найдя значение 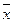, можно определить значение d. Наконец, значения

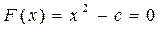и 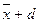используются в качестве начальных приближений для определения соответственно а₁ и а₂.

Конечно, и в этом случае можно не суметь отделить корни, если f"(x) близко к нулю. Это означает, что уравнение f'(х) = 1 имеет более, чем один корень вблизи 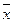. В этом случае сначала необходимо найти решение уравнения f"(х) = 0. Интересующийся читатель может найти необходимые сведения в книге Н. Мейкона.

Не нашли, что искали? Воспользуйтесь поиском: