
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Порог чувствительности
Характеристики измерительных систем
Мы рассмотрим здесь несколько характеристик измерительных систем, которые могут влиять на правильность результата измерения. Если один или большее число параметров, отражающих эти характеристики, не соответствуют требуемым (или заданным) значениям, то при измерении будут происходить ошибки.
Чувствительность
Чувствительность S (линейной) измерительной системы — это отношение величины выходного сигнала у к величине входного сигнала х
S =  .
.
Чувствительность измерительной системы, вообще говоря, зависит от частоты: S =  (ω).
(ω).
Чувствительность измерительного усилителя обычно называют усилением, тогда как в отношении (измерительных) систем в общем случае говорят о передаточной функции. Помимо чувствительности иногда используют масштабный коэффициент W, равный, по определению,
W=  .
.
Вот пример. Высота сетки на экране осциллографа равна 8 см. Электронный луч отклоняется на всю высоту сетки при наличии на входе осциллографа сигнала с полным размахом 40 мВ. Следовательно, чувствительность S составляет 0,2 см/мВ, а масштабный коэффициент Неравен 5 мВ/см. Именно масштабный коэффициент, как правило, бывает указан для осциллографов.
Когда передаточное соотношение у = f{x), связывающее выходной сигнал у (отсчет) и входной сигнал х (величину, которая должна быть измерена), является нелинейным, нельзя говорить о чувствительности, так как отношение выходного сигнала у ко входному сигналу х меняется в зависимости от величины х. Для таких нелинейных систем мы введем дифференциальную чувствительность. По определению, дифференциальная чувствительность S 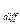 измерительной системы, описываемой соотношением у = f( x), при входном сигнале х
измерительной системы, описываемой соотношением у = f( x), при входном сигнале х 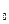 равна
равна
S 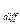 (x
(x 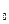 )=
)= 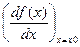 .
.
В случае линейной системы S 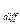
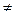 S
S 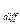 (x
(x 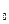 ) и S
) и S 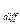 = S. У нелинейной системы S
= S. У нелинейной системы S 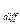 зависит от значения входного сигнала х.
зависит от значения входного сигнала х.
Возьмем, например, нуль-детектор с передаточной функцией у = ах — bx 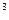 , где а > 0 и b > 0. Дифференциальная чувствительность такого устройства уменьшается с ростом входного сигнала. Для нуль-детектора особенно важно, чтобы дифференциальная чувствительность была высокой при очень малых входных сигналах. Чем больше S
, где а > 0 и b > 0. Дифференциальная чувствительность такого устройства уменьшается с ростом входного сигнала. Для нуль-детектора особенно важно, чтобы дифференциальная чувствительность была высокой при очень малых входных сигналах. Чем больше S 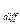 (0), тем лучше можно обнаружить выполнение нулевого условия и тем более точным может быть измерение.
(0), тем лучше можно обнаружить выполнение нулевого условия и тем более точным может быть измерение.
Другой мерой чувствительности нелинейной системы служит коэффициент чувствительности. Для измерительной системы с сигналом х на входе и сигналом у на выходе (с передаточным соотношением у = f( x)) коэффициент чувствительности S  определяется как
определяется как
S  =
=  .
.
Само обозначение S  указывает на то, что данный множитель характеризует чувствительность у к изменениям в х. В случае линейной системы S
указывает на то, что данный множитель характеризует чувствительность у к изменениям в х. В случае линейной системы S  является плохой мерой чувствительности, так как S
является плохой мерой чувствительности, так как S  = 1, какой бы ни была величина S.
= 1, какой бы ни была величина S.
Мы уже имели дело с коэффициентами чувствительности при обсуждении вопроса о распространении ошибок измерения (раздел 2.3.2). Другим примером использования коэффициента чувствительности в метрологии является тензодатчик. В этом датчике происходит преобразование изменения длины  в изменение сопротивления
в изменение сопротивления 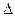 R. Коэффициент чувствительности тензодатчика S
R. Коэффициент чувствительности тензодатчика S  равен
равен
S  =
=  .
.
Отметим, что введенная выше чувствительность системы S является безразмерной только в том случае, когда у и х имеют одинаковую размерность. Это никогда не выполняется, например, в случае датчиков. У дифференциальной чувствительности S 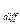 та же размерность, что и у чувствительности S. Однако, коэффициент чувствительности всегда безразмерен.
та же размерность, что и у чувствительности S. Однако, коэффициент чувствительности всегда безразмерен.
Порог чувствительности
Невозможно увеличивать чувствительность измерительной системы до бесконечности (например, путем увеличения коэффициента усиления): идя по этому пути, мы столкнемся с порогом чувствительности.
Порог чувствительности измерительной системы определяется как наименьший входной сигнал, который все еще обнаруживается с заданной вероятностью правильного решения. Порог чувствительности препятствует обнаружению нами сколь угодно малых сигналов. Это обусловлено тем, что во всякой реализуемой физической системе имеются спонтанные, случайные флуктуации (шум), из-за которых малый по величине измеряемый входной сигнал «тонет» в этом (образующем фон) шуме. Шум в измерительной системе может быть обусловлен многими причинами, такими как тепловые колебания (шум резистора) или квантовый характер потока зарядов, масс или носителей энергии через потенциальный барьер (дробовой шум электронов, ионов или фотонов).
Помимо принципиально неизбежных флуктуационных шумов в измерительной системе существуют и другие источники возмущений, которые могут затемнять полезный сигнал. Например, механические вибрации или электрические наводки могут давать настолько большой сигнал на выходе, что слабые сигналы, действующие на входе, уже нельзя обнаружить. Такие механические дефекты как трение, люфт или наличие мертвой зоны могут приводить к тому, что входной сигнал ниже определенного порога чувствительности не будет приводить к появлению сигнала на выходе. Часто простым изменением конструкции измерительной системы эти нефундаментальные ограничения можно устранить.
Принципиальный предел чувствительности системы определяется случайными флуктуациями внутри этой системы и является существенной характеристикой. В измерительной системе всегда присутствует шум, и он определяет теоретически осуществимый порог чувствительности.
Мы рассмотрим вопрос о пороге чувствительности шумящей измерительной системы в предположении, что измеряемая величина х остается постоянной. Пусть шум имеет гауссово распределение. Тогда при х = 0 выходной сигнал будет обладать плотностью распределения fn(x) с  = 0 (см. рис. 2.28). Если ко входу приложен сигнал х
= 0 (см. рис. 2.28). Если ко входу приложен сигнал х 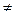 0, то выходной сигнал будет складываться из желаемого сигнала
0, то выходной сигнал будет складываться из желаемого сигнала  и (того же самого) шума. Плотность распределения в этом случае обозначим f
и (того же самого) шума. Плотность распределения в этом случае обозначим f  (y).
(y).
Теперь перед нами стоит важный вопрос: какой величины сигнал 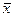 можно обнаружить? Другими словами, при каком значении
можно обнаружить? Другими словами, при каком значении  мы все еще можем отличить наблюдаемую ситуацию от случая, соответствующего
мы все еще можем отличить наблюдаемую ситуацию от случая, соответствующего 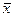 = 0 и, следовательно,
= 0 и, следовательно,  = 0? Ответ на этот вопрос зависит от степени определенности, с какой мы хотим знать, спрятан в шуме полезный сигнал или его нет. В постановке задачи нетрудно разобраться, следуя приводимым ниже рассуждениям. Предположим, что среднеквадратическое значение шума на выходе
= 0? Ответ на этот вопрос зависит от степени определенности, с какой мы хотим знать, спрятан в шуме полезный сигнал или его нет. В постановке задачи нетрудно разобраться, следуя приводимым ниже рассуждениям. Предположим, что среднеквадратическое значение шума на выходе  (стандартное отклонение распределения fn(y)) равно п-й части выходного сигнала
(стандартное отклонение распределения fn(y)) равно п-й части выходного сигнала  . В силу того, что плотность распределения вероятноcтей fn(y)
. В силу того, что плотность распределения вероятноcтей fn(y)

Рис.2.28. Порог чувствительности измерительной системы, подверженной действию шума, (а) Плотность распределения вероятностей для сигнала на выходе системы в отсутствие сигнала на входе (fn(y)) и при его наличии (fsn(y)). (b) Выходной сигнал как функция времени в случае, когда сигнала на входе нет (х = 0), и в случае, когда на входе действует сигнал, вызывающий появление на выходе постоянного напряжения  .
.
является четной функцией, мы можем ввести критерий обнаружения, основанный на том, что фактическое значение выходного сигнала у больше или меньше, чем 0,5  . Представим себе, что у- это выборочное значение выходного сигнала. Тогда нам необходимо иметь возможность сделать вывод о наличии сигнала
. Представим себе, что у- это выборочное значение выходного сигнала. Тогда нам необходимо иметь возможность сделать вывод о наличии сигнала  на основе единственной выборки у. (Когда мы можем позволить себе отложить принятие решения и взять среднее от нескольких выборок, это фактически означает осуществление низкочастотной фильтрации. В этом случае вероятность обнаружения значительно возрастает, так как увеличивается эффективное отношение сигнал/шум.) Если у > 0,5
на основе единственной выборки у. (Когда мы можем позволить себе отложить принятие решения и взять среднее от нескольких выборок, это фактически означает осуществление низкочастотной фильтрации. В этом случае вероятность обнаружения значительно возрастает, так как увеличивается эффективное отношение сигнал/шум.) Если у > 0,5  , то мы делаем вывод, что сигнал на входе присутствует, а если у < 0,5
, то мы делаем вывод, что сигнал на входе присутствует, а если у < 0,5  , то мы принимаем решение об отсутствии сигнала на входе. На рис. 2.28(b) показан случай, когда берется большое число выборок, как при наличии входного сигнала, так и в его отсутствие. Здесь п примерно равно 3 (
, то мы принимаем решение об отсутствии сигнала на входе. На рис. 2.28(b) показан случай, когда берется большое число выборок, как при наличии входного сигнала, так и в его отсутствие. Здесь п примерно равно 3 ( = З
= З  ). При п = 2 темная полоска между двумя изображениями выходного шума на экране осциллографа исчезает. В последнем случае мы уже не можем четко различать эти два изображения; на рис. 2.28(a) показаны соответствующие плотности распределения. Что значит надежность обнаружения в этом случае? Как можно видеть из графика на рис. 2.28(a), при
). При п = 2 темная полоска между двумя изображениями выходного шума на экране осциллографа исчезает. В последнем случае мы уже не можем четко различать эти два изображения; на рис. 2.28(a) показаны соответствующие плотности распределения. Что значит надежность обнаружения в этом случае? Как можно видеть из графика на рис. 2.28(a), при  = 2
= 2  (n = 2) (согласно критерию обнаружения, при котором происходит сравнение со значением 0,5
(n = 2) (согласно критерию обнаружения, при котором происходит сравнение со значением 0,5  ) заключение, что «входного сигнала нет», будет ошибочным для 16% выборок. Это в точности та часть всей площади под fsn(y), которая заштрихована. Поэтому доля случаев, в которых обнаруживается входной сигнал, порождающий выходной сигнал
) заключение, что «входного сигнала нет», будет ошибочным для 16% выборок. Это в точности та часть всей площади под fsn(y), которая заштрихована. Поэтому доля случаев, в которых обнаруживается входной сигнал, порождающий выходной сигнал  = 2, составляет 84%. Следовательно, с достоверностью 84% можно обнаруживать маскируемое шумом постоянное напряжение, когда среднеквадратическое значение шума равно половине значения этого постоянного напряжения (п =2). Отношение сигнал/шум в данном случае составляет (n
= 2, составляет 84%. Следовательно, с достоверностью 84% можно обнаруживать маскируемое шумом постоянное напряжение, когда среднеквадратическое значение шума равно половине значения этого постоянного напряжения (п =2). Отношение сигнал/шум в данном случае составляет (n  )2/
)2/  2 = п2 =4. Это рассуждение показывает, что желаемая степень надежности определяет порог чувствительности (значение n).
2 = п2 =4. Это рассуждение показывает, что желаемая степень надежности определяет порог чувствительности (значение n).
В табл. 2.3 приведена достоверность или вероятность обнаружения сигнала на входе по критерию y > 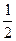
 , вычисленная для нескольких значений
, вычисленная для нескольких значений  .
.
 Табл. 2.3. Вероятность обнаружения и отношение сигнал/шум для различных значений сигнала
Табл. 2.3. Вероятность обнаружения и отношение сигнал/шум для различных значений сигнала  в зависимости от соотношения между стандартным отклонением
в зависимости от соотношения между стандартным отклонением  и величиной сигнала.
и величиной сигнала.
Общепринятой мерой порога чувствительности является величина входного сигнала, для которого отношение сигнал/шум равно единице. Тогда, в случае шума с нормальным распределением мгновенных значений, вероятность обнаружения оказывается равной примерно 70%.
В приведенном рассмотрении мы хотели выносить решение о наличии сигнала на входе по одному единственному выборочному значению или измерению. Порог чувствительности улучшается, когда мы выносим решение на основании нескольких (скажем, п ) выборок. Как мы уже видели,

 =
=  ,
,
где  -среднеквадратическое значение шума, а
-среднеквадратическое значение шума, а 
 - стандартное отклонение среднего от п выборок. Таким образом, в результате усреднения отношение сигнал/шум увеличивается в п раз и порог чувствительности соответственно снижается.
- стандартное отклонение среднего от п выборок. Таким образом, в результате усреднения отношение сигнал/шум увеличивается в п раз и порог чувствительности соответственно снижается.
Порог чувствительности можно также улучшить, сужая ширину полосы В измерительной системы. В предположении, что шум белый, находим его среднеквадратическое значение  :
:
 =
=  0
0  ,
,
где  0 - эквивалентный шум в полосе 1 Гц. Это означает, что с сокращением полосы В измерительной системы в какое-то число раз, во столько же раз увеличивается отношение сигнал/шум. Соответственно этому снижается порог чувствительности.
0 - эквивалентный шум в полосе 1 Гц. Это означает, что с сокращением полосы В измерительной системы в какое-то число раз, во столько же раз увеличивается отношение сигнал/шум. Соответственно этому снижается порог чувствительности.
В качестве альтернативы нахождению среднего от п отдельных последовательных выборок мы можем также измерять входной сигнал x(t) непрерывно в течение определенного времени T. Среднее по времени значение yavg выходного сигнала измерительной системы y(t) на интервале (t, t + T) равно:
yavg=  .
.
Теперь можно воспользоваться этим средним, чтобы установить, имеется сигнал на входе или его нет. Чтобы определить результирующее улучшение порога чувствительности, применим теорему Шеннона о выборках, которая звучит так: если у сигнала y(t) нет составляющих на частотах выше, чем В Гц, то этот сигнал полностью определяется выборками, взятыми с интервалом 1 / 2 В секунд на отрезке времени T, много большем чем 1 / В. Число дискретных выборок, описывающих y(t) на отрезке T секунд, равно 2ТВ. Возьмем среднее от этих 2 ТВ выборок. Среднеквадратическое значение шума в сигнале y(t) равно  =
=  0
0  . Таким образом, стандартное отклонение
. Таким образом, стандартное отклонение  avg среднего по выборкам из сигнала y{t) на протяжении Т секунд имеет вид:
avg среднего по выборкам из сигнала y{t) на протяжении Т секунд имеет вид:
 avg =
avg = 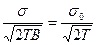 .
.
Следовательно, вычисление среднего на интервале времени Т приводит к увеличению отношения сигнал/шум в 2 T раз; порог чувствительности снижается  раз.
раз.
Подводя итоги, мы можем утверждать, что порог чувствительности — это наименьший сигнал, который можно обнаружить с определенной степенью достоверности на фоне собственного шума измерительной системы. Порог чувствительности зависит от требуемой достоверности и величины шума в измерительной системе. Шум можно уменьшить, применяя измерительную систему с меньшей шириной полосы или вычисляя среднее для ряда выборочных значений, полученных в результате измерений, а также путем нахождения среднего по времени при непрерывном измерении на интервале времени T. Все эти меры требуют затраты большого времени для получения результата; как следствие их применения, отклик измерительной системы становится более медленным, и это является платой за снижение собственного порога чувствительности измерительной системы.
Не нашли, что искали? Воспользуйтесь поиском: