РЕГРЕССИОННЫЙ АНАЛИЗ

Предположим, что в результате вероятностного эксперимента E фиксируются две случайные величины X и Y. Тогда между X и Y может существовать статистическая зависимость.

Статистической зависимостью между СВ Х и СВ Y называется правило, которое каждому числу x Î Х ставит в соответствие условное распределение Y.

Пример 8. Пусть X - рост человека, Y - размеры обуви. Величина Х распределена на интервале 0,5м - 2,50 м. Каждому x Î Х соответствует некоторое распределение размеров обуви. Возьмем рост x = 175см, тогда, например, 37% людей с данным ростом имеет размер обуви 42, 25% - размер обуви 43 и так далее. Рассматривать для каждого значения x Î Х все распределение F(Y/X) на практике неудобно, поэтому вместо всего распределения обычно рассматривают математическое ожидание этого распределения, т.е. M(Y/X).

Зависимость среднего значения некоторой случайной величины от другой величины называют регрессией.

Заметим, что регрессия является обычной функциональной зависимостью. Уравнение регрессииимеет вид

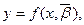(12)

где 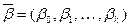- совокупность некоторых параметров

Для получения уравнения (12) необходимо иметь всю информацию о ГС. На практике такой информации обычно нет, есть только выборка, состоящая из n пар (x_i, y_i). На основании этой информации получают эмпирическое уравнение регрессии, являющееся некоторой оценкой уравнения (12)

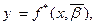(13)

где .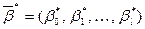

Для получения уравнения (13) поступают следующим образом

1) Результаты наблюдений (x_i, y_i) изображают в виде точек в декартовой или иной системе координат. Полученная точечная диаграмма называется корреляционным полем. С помощью корреляционного поля или других соображений выдвигается гипотеза о виде функции (13).

2) С помощью метода наименьших квадратов (МНК) или метода наибольшего правдоподобия находят по данным выборки значения параметров .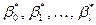

3) Проверяют согласие эмпирического уравнения регрессии с экспериментальными значениями.

Рассмотрим наиболее простой случай - линейную регрессию. В этом случае уравнение (13) примет вид

Y_x = + x. (14)

Найдем коэффициенты и по методу наименьших квадратов. Для этого рассмотрим сумму квадратов отклонений эмпирических значений y _i от предполагаемых теоретических (описываемых формулой (14)).

Подберем неизвестные параметры и так, чтобы функция S( , ) приняла минимальное значение. Для этого можно воспользоваться методами дифференциального исчисления. После ряда выкладок (см./2, 3/) получается линейная система уравнений для определения и :

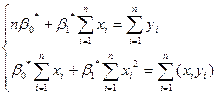(15)

Решая эту систему, находим значения и . Подставляя эти значения в уравнение (14), получаем эмпирическое уравнение регрессии.

Затем с помощью эмпирического коэффициента корреляции или с помощью других статистик проводится проверка согласия полученного уравнения с экспериментальными данными (см./2, 3, 6/).

4 ДИСПЕРСИОННЫЙ АНАЛИЗ

Дисперсионным анализом называется раздел математической статистики, в котором проводится анализ количественных результатов, зависящих от качественных факторов. К примеру, дисперсионный анализ может быть использован для выявления совместного влияния экономических факторов, не поддающихся количественному измерению, на изучаемый экономический показатель и так далее.

Рассмотрим ряд примеров.

Пример 9. Пусть проводилось выборочное обследование производительности труда рабочих одинаковых профессий пяти ателье по ремонту обуви. Производительность выражена в относительных единицах по отношению к базовой, принятой за единицу. Требуется установить, существенно ли различаются средние значение производительности труда в этих ателье. Здесь количественный фактор – производительность труда зависит от качественного фактора – принадлежности групп рабочих к тому или иному предприятию, этот фактор имеет пять уровней. Если выяснится, что различие существенно, то в дальнейшем могут быть выявлены причины этого с целью повышения производительности труда в отстающих ателье.

Пример 10. Пусть выпускается один и тот же фасон платья из одной и той же ткани, но 6 разных цветов. Можно провести статистическое исследование спроса на эти платья в зависимости от цвета. Здесь качественный фактор – цвет платья, у этого фактора 6 уровней. Количественным фактором будет спрос на платья, данного цвета. Если выяснится, что фактор – цвет является существенным, можно изменить план производства, подстраиваясь под спрос, что приведет к улучшению экономических показателей предприятия.

Пример 11. Пусть в примере 2 выпускаются платья 6 ^ти разных цветов и 5 ^ти разных фасонов, все остальное такое же. Тогда у нас два качественных признака (фактора) – цвет и фасон и один количественный – спрос. В этом случае мы имеем дело с двухфакторным дисперсионным анализом. У первого фактора 6 уровней, у второго 5 уровней. Очевидно, что данный пример легко обобщается и можно рассматривать трехфакторную, четырехфакторную и так далее модели.

Метод дисперсионного анализа позволяет проверить, оказывают ли влияние на математическое ожидание случайных величин определенные факторы, которые можно произвольно изменять в ходе эксперимента, выбирать наиболее важные из них и оценивать степень их влияния.

Если на математическое ожидание оказывает влияние только один фактор, то соответствующей критерий значимости называется однофакторным дисперсионным анализом. Идея однофакторного дисперсионного анализа заключается в разбиении общей дисперсии случайной величины Х на два независимых слагаемых – факторную дисперсию и остаточную дисперсию. Факторная дисперсия порождается действием исследуемого фактора А, остаточная дисперсия зависит от ряда других факторов. Таким образом

D_общ=D_факт+D_ост (16)

Если влияние исследуемого фактора существенно, то доля D_факт в D_общ достаточно велика. Сравнение факторной и остаточной дисперсии проводят с помощью критерия Фишера.

Рассматривается отношение

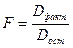(17)

Чем больше это отношение, тем большее влияние оказывает фактор А на результат, если же это отношение близко к нулю, то влияние фактора малосущественное и им можно пренебречь. Это несколько неточное рассуждение будет уточнено в дальнейшем.

Сформулируем основные предположения и ограничения, лежащие в обосновании дисперсионного анализа в виде вероятностной модели.

Пусть некоторый количественный результат, по нашему предположению, зависит от некоторого качественного фактора А. Пусть фактор А может принимать к разных уровней (уровней, а не значений!). Результаты экспериментов разобьем на к групп в зависимости от уровней фактора. В каждую группу входят все эксперименты, отвечающие данному уровню фактора. Пусть количество экспериментов в каждой группе n _i, i = 1,2 ,…,k. Обозначим результаты измерений через x_ij, где i – номер уровня фактора, j – номер результата измерения на данном уровне. Результаты измерения на каждом уровне i будем рассматривать как выборку из генеральной совокупности X _i, распределенной по нормальному закону: X _iÎ N (a_i, s_i). Параметры a_i, s_i неизвестны, но предполагается, что 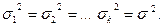Выполнение этого равенства можно проверить по критерию Бартлетта /см 2/.

Представим результаты измерений х_ij в виде суммы двух слагаемых: x_ij=a_i+e_ij, где a_i – математическое ожидание случайной величины Х_i, e_ij – случайная ошибка (остаток) характеризующая влияние на результаты x_ij неучтенных и случайных факторов. Предполагается, что, e_ij распределены нормально, точнее e_ij Î N( 0, s). В качестве e_ij можно рассматривать отклонение от средних размеров, вызванных действием многочисленных малых источников погрешностей, в том числе отклонение физико-химических свойств заготовок от номинала, биения вибраций механической части оборудования, вариации параметров электрической части оборудования, погрешности в работе электронной управляющей части и т.п.

Далее вычисляем по выборочным данным следующие величины.

1) Групповые средние арифметические

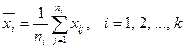(18)

2) Общую среднюю арифметическую

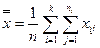(19)

3) Факторную дисперсию по формуле

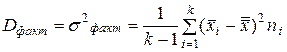(20)

4) Остаточную дисперсию по формуле

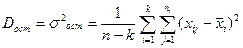(21)

5) Выборочную статистику F_набл по формуле

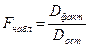
Теперь на основе имеющейся информации можно проверить нулевую гипотезу Н ₀ – все математические ожидания одинаковые, против альтернативной гипотезы Н_а – не все математические ожидания равны между собой.

Приступим к проверке нулевой гипотезы Н ₀. Зададимся уровнем значимости и найдем табличное значение F_табл(a, v ₁, v ₂ ), где v ₁ =k- 1, v ₂= n-k. Таблицы функции F (распределение Фишера) есть практически во всех учебниках по теории вероятностей и математической статистике. Величины v ₁ и v ₂ называются степенями свободы. Если F_набл ³ F_табл(a, v ₁, v ₂ ) то нулевая гипотеза Н ₀ отклоняется, то есть считается, что фактор А является существенным. Если F_набл< F_табл(a, v ₁, v ₂ ), то принимается нулевая гипотеза, то есть считается, что фактор А не оказывает влияние на результат и им можно пренебречь.

Не нашли, что искали? Воспользуйтесь поиском: