
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Контрольная работа № 2.
1. Определённый интеграл и его приложения.
2. Несобственный интеграл.
3. Двойной интеграл.
4. Дифф. уравнения 1 порядка с разделяющимися переменными.
Варианты для самостоятельного решения:
Вариант 1.
1.Вычислить площадь области, ограниченной кривыми:
 ,
,  ,
,  .
.
2. Найти несобственный интеграл  .
.
3. Найти двойной интеграл  , где
, где  - треугольник с вершинами (0,0), (1,1), (1,3).
- треугольник с вершинами (0,0), (1,1), (1,3).
4. Решить дифф. уравнение 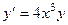 .
.
Вариант 2.
1.Вычислить площадь области, ограниченной кривыми:
 ,
, 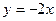 ,
,  .
.
2. Найти несобственный интеграл  .
.
3. Вычислить в полярных координатах интеграл от функции  по 1-й четверти круга радиуса 1.
по 1-й четверти круга радиуса 1.
4. Дифф. уравнение 1 порядка 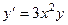 .
.
Аналогичные задачи из практических занятий:
Задача 1.1. Вычислить 
Решение.  =
= 
здесь мы можем заменить  на
на  , но тогда нужно сделать пересчёт верхнего и нижнего пределов. Если
, но тогда нужно сделать пересчёт верхнего и нижнего пределов. Если  то
то  , т.е.
, т.е.  .
.
 =
=  =
= 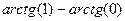 =
=  =
=  .
.
А можно было сначала вычислять интеграл как неопределённый, тогда надо было бы вернуться к исходной переменной  (то есть сделать обратную замену), но пределы можно не пересчитывать.
(то есть сделать обратную замену), но пределы можно не пересчитывать.
 =
=  =
=  =
= 
 =
=  =
= 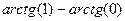 =
=  .
.
Ответ.  .
.
Задача 1.2. Найти площадь области, ограниченной линиями 
Решение.
 =
=  =
= 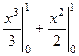 =
= 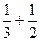 =
=  .
.

Ответ.  .
.
Задача 2. Найти несобственный интеграл  .
.
Решение.  =
=  =
=  =
=
 =
=  =
=  .
.
Здесь под символом  понимается предел
понимается предел  .
.
Ответ.  .
.
Задача 3.1. Вычислить интеграл  по треугольнику D, вершины которого: (0,0),(1,0),(0,1).
по треугольнику D, вершины которого: (0,0),(1,0),(0,1).
Решение. Строение треугольника понятно (см. чертёж).
Наклонная линия задаётся уравнением  .
.

Вычисление: 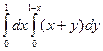 =
=  =
=
 =
=  =
=  =
=
 =
=  . Ответ.
. Ответ. 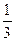 .
.
Задача 3.2. Вычислить  , где D - четверть круга радиуса 1 (в первой координатной четверти).
, где D - четверть круга радиуса 1 (в первой координатной четверти).
Решение. Заменим  ,
,  , а также умножим на якобиан
, а также умножим на якобиан  .
.

 =
=  =
=
 =
= 
Дальше остаётся интеграл от одной переменной, там можно применять обычный способ, подведение под знак дифференциала.
 =
=  =
=  =
= 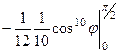 =
=  =
=  .
.
Ответ.  .
.
Задача 4. Решить уравнение  .
.
Решение. 





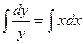





 .
.
Ответ.  .
.
Проверка. Если  , то
, то  , действительно, производная имеет лишний множитель
, действительно, производная имеет лишний множитель  по сравнению с исходной функцией, и подходит в качестве решения уравнения
по сравнению с исходной функцией, и подходит в качестве решения уравнения  .
.
Не нашли, что искали? Воспользуйтесь поиском: