Производная сложной функции двух переменных

Пусть 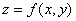– функция двух переменных и каждая из них является функцией от переменной : .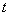

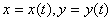Тогда 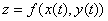– сложная функция переменной .

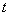Теорема 26.4.

Если функции 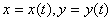дифференцируемые в точке ,

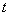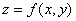– дифференцируема в точке 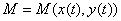, то сложная функция 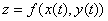также дифференцируема в точке 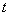. При этом:

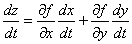(26.4)

Пример 26.4.

1)

.

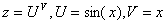
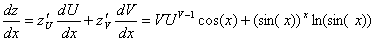2)

.

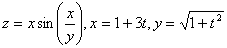
Замечание 3.

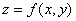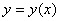Если и , то .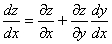

Градие́нт (от лат. gradiens, род. падеж gradientis — шагающий, растущий) — вектор, своим направлением указывающий направление наискорейшего возрастания некоторой величины 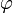, значение которой меняется от одной точки пространства к другой (скалярного поля), а по величине (модулю) равный быстроте роста этой величины в этом направлении.

Например, если взять в качестве 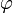высоту поверхности Земли над уровнем моря, то её градиент в каждой точке поверхности будет показывать «направление самого крутого подъёма», и своей величиной характеризовать крутизну склона.

Для случая трёхмерного пространства градиентом скалярной функции 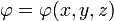координат , , 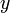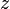называется векторная функция с компонентами

, , .

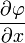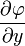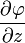Или, использовав для единичных векторов по осям прямоугольных декартовых координат :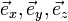

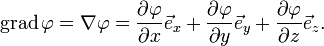
Если 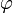— функция переменных 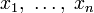, то её градиентом называется -мерный вектор

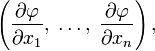
компоненты которого равны частным производным 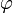по всем её аргументам.

• Размерность вектора градиента определяется, таким образом, размерностью пространства (или многообразия), на котором задано скалярное поле, о градиенте которого идет речь.
• Оператором градиента (обозначаемым обычно, как говорилось выше, 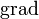или ) называется оператор, действие которого на скалярную функцию (поле) дает ее градиент. Этот оператор иногда коротко называют просто "градиентом".

Смысл градиента любой скалярной функции 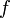в том, что его скалярное произведение с бесконечно малым вектором перемещения 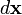дает полный дифференциал этой функции при соответствующем изменении координат в пространстве, на котором определена 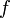, то есть линейную (в случае общего положения она же главная) часть изменения 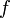при смещении на 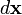. Применяя одну и ту же букву для обозначения функции от вектора и соответствующей функции от его координат, можно написать:

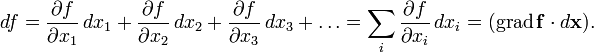
Стоит здесь заметить, что поскольку формула полного дифференциала не зависит от вида координат 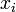, то есть от природы параметров x вообще, то полученный дифференциал является инвариантом, то есть скаляром, при любых преобразованиях координат, а поскольку 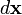— это вектор, то градиент, вычисленный обычным образом, оказывается ковариантным вектором, то есть вектором, представленным в дуальном базисе, какой только и может дать скаляр при простом суммировании произведений координат обычного (контравариантного), то есть вектором, записанным в обычном базисе. Таким образом, выражение (вообще говоря — для произвольных криволинейных координат) может быть вполне правильно и инвариантно записано как:

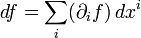
или, опуская по правилу Эйнштейна знак суммы,

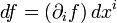
(в ортонормированном базисе мы можем писать все индексы нижними, как мы и делали выше). Однако градиент оказывается настоящим ковариантным вектором в любых криволинейных координатах.

линией уровня функции называется множество точек из ее области определения, в которых функция принимает одно и то же фиксированное значение. Градиентом функции f(x) называется вектор

Δ f(x) = df,…, df

dx ₁ dx_n

указывающий направление наиболее быстрого возрастания функции, и, стало быть, ориентированный перпендикулярно линиям уровня.

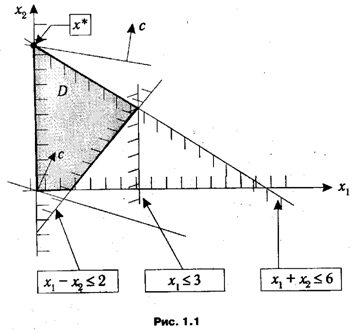
Для линейной функции двух переменных линия уровня представляет собой прямую, перпендикулярную вектору с, который служит градиентом данной функции. Следовательно, если линия уровня определяется уравнением f(x)=c₁x₁+ c₂x₂ =const, то этот вектоp имеет вид

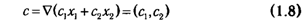
и указывает направление возрастания функции.

Таким образом, с геометрической точки зрения задача максимизации сводится к определению такой точки области D, через которую проходит линия уровня, соответствующая наибольшему из возможных значений. Последнее означает, что для нахождения точки экстремума в задаче линейного программирования мы должны сначала построить линию уровня для некоторого произвольного значения целевой функции. Затем необходимо осуществлять ее параллельное передвижение (так, чтобы она оставалась перпендикулярной вектору с) до тех пор, пока не достигнем такой точки области допустимых планов D, из которой смещение в направлении вектора с было бы невозможно. Такой метод решения получил название графического. Заметим, что решение задачи поиска минимума линейной функции осуществляется аналогично, с той лишь разницей, что движение по линиям уровня должно производиться в направлении, обратном градиенту целевой функции, т. е. по вектору (-с).

На рис. 1.1 изображен некоторый частный случай, для которого решение ЗЛП достигается в угловой точке х* = (0, 6) области D. Нетрудно представить, что возможны и другие варианты. Они изображены на рис. 1.2.

Рисунок (а) иллюстрирует ситуацию неограниченности целевой функции f(x)=cx на множестве D, т.е. сколько бы мы ни перемещались по линиям уровня в направлении вектора с, ее значение будет возрастать.

В случае, изображенном на рисунке (b), линия уровня, соответствующая максимальному значению f(x), касается грани множества D, и, соответственно, все точки, лежащие на этой грани, являются оптимальными планами.

Во всех рассмотренных иллюстрациях допустимые планы ЗЛП представлялись в виде некоторого многогранного выпуклого множества на плоскости. Такое их представление в литературе получило название первой геометрической интерпретации задачи линейного программирования.

Не нашли, что искали? Воспользуйтесь поиском: