
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Розділ 2. Логічні основи ЕОМ
2.1 Алгебра логіки (АЛ)

Операція – це чітко визначена дія над одним або декількома операндами, яка створює новий об’єкт (результат).
Основними булевими операціями є заперечення, кон'юнкція, диз'юнкція, які можна задати за допомогою таблиць істинності.
Запереченням висловлювання А є таке висловлювання, яке істинне, коли А хибне, і хибне, коли А істинне. Воно позначається через  і читається «не А». Заперечення розповсюджується на один операнд.
і читається «не А». Заперечення розповсюджується на один операнд.
Таблиця 2.1. Логічні значення операції заперечення
| А | 
|
Кон'юнкція двох висловлювань є складне висловлювання. Вона відноситься до групи бінарних операцій. У разі істинності обох висловлювань істинна і сама кон'юнкція, інакше вона помилкова. Вона також помилкова, якщо помилкове будь-яке з двох висловлювань. У загальному випадку число висловлювань може бути і більше двох. Операція кон'юнкції позначається «А^В» і читається «А і В». Кон'юнкцію також називають логічним множенням і позначають знаком &.
Таблиця 2.2. Логічні значення операції кон'юнкції
| A | B | A^B |
Диз'юнкція двох висловлювань – складний, бінарний, вислів. Вона хибна у разі помилковості обох складових її висловлювань і істинна в решті випадків. Диз'юнкція позначається AVB або А+В і читається «А або В». Інша назва цієї операції – логічне додавання.
Таблиця 2.3. Логічні значення операції диз'юнкції
| A | B | AVB |
Для булевих операцій заперечення, диз'юнкції і кон'юнкції справедливі такі закони, властивості й тотожності:
· комутативність (переміщувальний закон):
Х1+X2=X2+X1;
Х1•X2=X2•X1;
· асоціативність (сполучний закон):
Х1(Х2+X3)=Х1Х2+Х1Х3;
Х1+(Х2X3)=(Х1+X2)(Х1+X3);
· закон поглинання:
Х1+X1X2=X1;
Х1(Х1+X2)=Х1;
· закон склеювання:
Х1X2+X1=X1;
(Х1+X2)(Х1+  )=Х1;
)=Х1;
· властивості заперечення і констант:
 Х+0=X; Х•0=0;
Х+0=X; Х•0=0;
Х+1=1; Х•1=X;  ;
;
· закон де Моргана:
 ;
;
 ;
;
Будь-який складний вираз, утворений з простих висловлювань, називається формулою АЛ. Дві формули АЛ, утворені з n простих висловлювань А1, А2, Аn, називаються рівносильними в тому випадку, якщо для кожної з цих комбінацій обидві формули АЛ матимуть однакові значення істинності. Оскільки існують в точності  різних комбінацій значень істинності n простих висловлювань і для кожної з цих
різних комбінацій значень істинності n простих висловлювань і для кожної з цих  комбінацій складний вираз може бути або істинним, або помилковим, то може бути
комбінацій складний вираз може бути або істинним, або помилковим, то може бути  різних функцій АЛ, які можуть бути побудовані з n даних простих висловлювань. Зокрема, для двох двійкових змінних можна побудувати 16 різних висловлювань АЛ, тобто скласти 16 нерівносильних складних логічних виразів. Ці вирази містять усі описані раніше логічні зв'язки (заперечення виключається, оскільки це функція однієї змінної).
різних функцій АЛ, які можуть бути побудовані з n даних простих висловлювань. Зокрема, для двох двійкових змінних можна побудувати 16 різних висловлювань АЛ, тобто скласти 16 нерівносильних складних логічних виразів. Ці вирази містять усі описані раніше логічні зв'язки (заперечення виключається, оскільки це функція однієї змінної).
Логічні операції кон'юнкції, диз'юнкції, співвідношення, еквівалентності, заперечення еквівалентності (^,V,--,  ,~,
,~,  ) не є незалежними, і можуть бути виражені одина через одну. Зокрема з них можна виділити системи логічних операцій із їхньою допомогою представити взагалі усі функції АЛ. Це системи: --,^,V, або --,^, або --,V. Крім того, існує операція заперечення кон'юнкції
) не є незалежними, і можуть бути виражені одина через одну. Зокрема з них можна виділити системи логічних операцій із їхньою допомогою представити взагалі усі функції АЛ. Це системи: --,^,V, або --,^, або --,V. Крім того, існує операція заперечення кон'юнкції  , через яку (одну) може бути виражена будь-яка функція АЛ. Усі перераховані системи вважаються функціонально повними. Зокрема операція
, через яку (одну) може бути виражена будь-яка функція АЛ. Усі перераховані системи вважаються функціонально повними. Зокрема операція  , що стверджує несумісність двох висловлювань, позначається A|B і називається функцією Шеффера, при цьому заперечення, кон'юнкція і диз'юнкція виражаються так:
, що стверджує несумісність двох висловлювань, позначається A|B і називається функцією Шеффера, при цьому заперечення, кон'юнкція і диз'юнкція виражаються так:  ,
,  ,
,  .
.
Електронна схема, що реалізує операцію Шеффера, є функціональним універсальним елементом. За її допомогою можуть бути побудовані будь-які функціональні схеми дискретних автоматів.
Довільну булеву функцію можна задавати різними способами: словесним описанням, часовими діаграмами, геометричними фігурами, графами, таблицями істинності та аналітичними виразами.
Словесний опис деякої булевої функції F(X1, Х2) можна представити так: F=1 при X1Х2=1 і F=0, якщо X1Х2=0. Таку функцію можна зобразити часовою діаграмою (рис. 2.2, а) або геометрично за допомогою двовимірного куба, у якому точками виділені одиничні вершини (дана функція набуває значення одиниці на наборі <1, 1>) (рис. 2.2, б), а також графом, де вершини відображають значення нуля і одиниці, а на орієнтованих дугах змінні вказують на умови переходів (рис. 2.2, в).
 |
Рис. 2.2. Способи задавання булевих функцій
До нових булевих функцій (операцій) відносяться такі.
Еквівалентність двох висловлювань – бінарний вислів. Вона істинна тоді, коли значення істинності висловлювань однакові і хибна навпаки. Позначається А~В і читається «А еквівалентно В».
Таблиця 2.4. Логічні значення операції еквівалентністі
| A | B | A~B |
Сума за модулем два (виключальне АБО, заперечення еквівалентності) двох висловлювань є бінарним висловом, яка хибна у тому випадку, коли А і В мають різні значення.
Таблиця 2.5. Логічні значення операції заперечення еквівалентності
| A | B | A  B B
|
Імплікація двох висловлювань є бінарним висловом, яка хибна тільки у тому випадку, коли А істинне, а В помилкове. Її позначають через  , і читається так «якщо А, то В». Імплікація не припускає обов'язковий зв'язок по сенсу між умовою А і слідством В (хоча і не виключає такий зв'язок).
, і читається так «якщо А, то В». Імплікація не припускає обов'язковий зв'язок по сенсу між умовою А і слідством В (хоча і не виключає такий зв'язок).
Таблиця 2.6. Логічні значення операції імплікації
| A | B | 
|
Булеві функції одного і двох аргументів називають елементарними. Схему, яка здійснює елементарну логічну операцію, називають логічним елементом. Сукупність взаємозалежних елементів з формальними методами описання називається логічною схемою.
Для реалізації однієї і тієї ж логічної функції існує велика кількість різних електронних схем. З метою спрощення документації були введені символи, так звані логічні елементи, які позначають тільки логічну функцію і не розкривають внутрішню будову схеми.
Основні логічні елементи мають, як правило, один вихід (Y) та декілька входів, число яких дорівнює числу аргументів (Х1, Х2, Х3,…, Хn). На електричних схемах логічні елементи зображуються у вигляді прямокутників з виводами для вхідних (ліворуч) і вихідних (праворуч) змінних. Всередині прямокутника зображується символ, який вказує на функціональне призначення елемента.
Назви і умовні графічні позначення основних логічних функцій, які застосовуються в комп’ютерній схемотехніці наведені нижче:
Операція кон'юнкція реалізується логічним елементом «І»
 |
Операція диз'юнкція реалізується логічним елементом «АБО»
 |
Операція заперечення реалізується логічним елементом «НІ»
 |
 Операція заперечення еквівалентністі реалізується логічним елементом «Виключальне АБО»
Операція заперечення еквівалентністі реалізується логічним елементом «Виключальне АБО»
Операція еквівалентность реалізується логічним елементом
 |
Операція імплікація реалізується логічним елементом
 |
Операція заборона реалізується логічним елементом
 |
Рядом з однофункціональними елементами (І, АБО, НІ), широко використовуються двофункціональні (АБО-НІ, І-НІ)
 АБО-НІ І-НІ
АБО-НІ І-НІ
Будь-яку логічну функцію можна реалізувати на логічних елементах. Наприклад 
 |
Рис. 2.1. Схема для реалізації логічної функції  .
.
Приклад. Необхідно скласти схему, на виході якої при В>А, де А і В є однозначними двійковими цифрами, встановлюється логічна одиниця 1. Складаємо табл. 2.7.
Таблиця 2.7
| А | В | Y |
З таблиці маємо, що Y=1 при виконанні тільки однієї умови, коли А=0 і В=1. Логічна функція записується у вигляді  . Вона реалізується на таких логічних елементах:
. Вона реалізується на таких логічних елементах:
 |
Рис. 2.3. Схема для реалізації логічної функці  .
.
Теорема Шеннона
Широке використання під час перетворення логічних функцій знаходять теорема Шеннона та ряд тотожностей, які випливають з неї.
Теорема Шеннона формулюється у такий спосіб: будь-яку функцію п змінних можна записати у вигляді:

(2.4)
Теорема Шеннона виявляється дуже корисною при виконанні перетворень логічних виразів, що містять операцію виключальне АБО.
Приклад. Виконати перетворення логічної функції:

Розв'язання. Використовуючи теорему Шеннона, виконуємо такі перетворення:

З теоремою Шеннона (2.4) пов'язані тотожності:

 (2.5)
(2.5)
Виходячи з теореми де Моргана, тотожностям (1.9) відповідають такі тотожності:
 (2.6)
(2.6)
Тотожності (2.5) і (2.6) широко використовуються для спрощення логічних виразів. З них випливають формули:

Наведені тотожності дозволяють суттєво спрощувати складні функції багатьох змінних, особливо за наявності заперечень.
 Приклад. Спростити логічну функцію:
Приклад. Спростити логічну функцію:
Розв'язання. Використовуючи тотожність (1.8) відносно  , маємо:
, маємо:
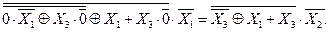
З тотожності (1.9) знаходимо:

У результаті визначаємо:
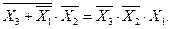
Подані вище тотожності використовуються для того, щоб розкладати складні логічні функції на більш прості.
Не нашли, что искали? Воспользуйтесь поиском: