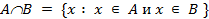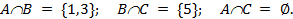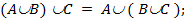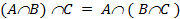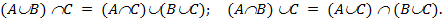Оценка производительности

Наибольшая эффективность расчета методом факторизации Ферма достигается в случае, когда множители числа 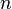примерно равны между собой. Это обеспечивает относительно короткий поиск последовательности ^[5]

В наихудшем варианте, когда, к примеру, близко к 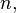а близко к 1, алгоритм Ферма работает хуже по сравнению с методом перебора делителей. Число итераций для данного случая:

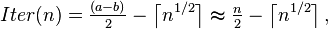т.е., очевидно, что оно имеет порядок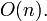

Метод факторизации Ферма будет работать не хуже метода перебора делителей, если 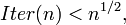отсюда можно получить оценку для большего делителя Следовательно, метод Ферма имеет экспоненциальную оценку и, как метод пробного деления, не подходит для разложения больших чисел. Можно повысить эффективность, если выполнить сначала пробное деление числа 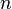на числа от 2 до некоторой константы B. После этого, выполнить поиск делителей методом Ферма. Такой поход помогает избавиться от малых делителей числа 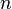^[6].

можно легко факторизовать.

Действительно: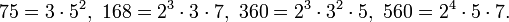

Очевидно, что произведение полученный четырех чисел будет квадратом: Тогда теперь можно вычислить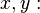

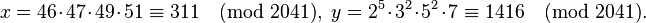
Далее с помощью алгоритма Евклида находим .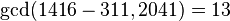

Таким образом,

И 6 вопросы

Определение. Объединением (суммой) двух множеств A и B называется множество (его принято обозначать 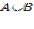) состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из этих множеств - либо A, либо B.

На языке кванторов мы будем записывать эту операцию следующим образом:

Пример. Рассмотрим множества A = {1, 2, 3, 4}, B = {1,3,5}, C = {5,6}. Тогда, согласно введенному определению получаем:

Аналогично определяется объединение (сумма) множеств A1,A2,..., An. Объединением этих множеств называется множество, обозначаемое 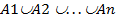, состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из этих множеств.

Достаточно часто для наглядного изображения этих операций над множествами используют, так называемые, круги Эйлера (диаграммы Венна). Множества при таком подходе изображают кругами, а результат операции закрашивают или заштриховывают. Вот так выглядит результат операции объединения двух множеств.

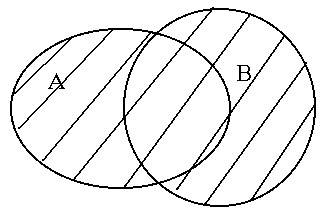
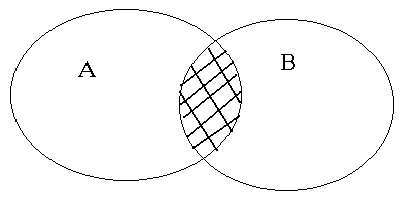
Определение. Пересечением (произведением) двух множеств A и B называется множество (его принято обозначать 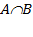) состоящее из всех тех и только тех элементов, которые принадлежат каждому из множеств A и B.

На языке кванторов мы будем записывать эту операцию следующим образом:

Пример. В рамках введенных в предыдущем примере определений множеств A, B, C мы получаем:

Также как мы делали раньше, можно определить пересечение (произведение) конечного числа множеств.

На кругах Эйлера пересечение множеств выглядит следующим образом:

Бывает удобно ввести понятие "универсального" множества U, которое по предположению содержит все используемые нами множества.
Введенные операции над множествами обладают свойствами коммутативности:

и свойством ассоциативности:

справедливость этих свойств следует из самих определений операций пересечения и объединения множеств, поэтому, обычно, скобки в таких групповых операциях опускают.
Имеет место также закон взаимной дистрибутивности:

Перейдем к новой операции над множествами. Эта операция определяется только для двух множеств.

Круги́ Э́йлера ^[1] — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Изобретены Леонардом Эйлером. Используется в математике, логике, менеджменте и других прикладных направлениях.

Важный частный случай кругов Эйлера — диаграммы Эйлера — Венна, изображающие все 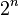комбинаций 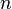свойств, то есть конечную булеву алгебру. При 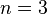диаграмма Эйлера — Венна обычно изображается в виде трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.

При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов. Однако этим методом ещё до Эйлера пользовался выдающийся немецкий философ и математик Готфрид Вильгельм Лейбниц. Лейбниц использовал их для геометрической интерпретации логических связей между понятиями, но при этом всё же предпочитал использовать линейные схемы.^[2]

Пример получения произвольных кругов Эйлера из диаграмм Венна с пустыми (чёрными) множествами

Но достаточно основательно развил этот метод сам Л. Эйлер. Методом кругов Эйлера пользовался и немецкий математик Эрнст Шрёдер в книге «Алгебра логики». Особенного расцвета графические методы достигли в сочинениях английского логика Джона Венна, подробно изложившего их в книге «Символическая логика», изданной в Лондоне в 1881 году. Поэтому такие схемы иногда называют Диаграммы Эйлера — Венна.

Вопрос

Не нашли, что искали? Воспользуйтесь поиском: