
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Нормалью к поверхности S в точке M0 называется прямая, проходящая через точку M0 и перпендикулярная касательной плоскости к поверхности S в точке M0 .
Из определения нормали следует, что нормальный вектор  = (A;B;C)касательной плоскости будет направляющим вектором нормали. Следовательно, канонические уравнения нормали к поверхности S в точке M0 будут иметь вид
= (A;B;C)касательной плоскости будет направляющим вектором нормали. Следовательно, канонические уравнения нормали к поверхности S в точке M0 будут иметь вид
 .
.
Пример. Написать уравнение касательной плоскости и нормали к поверхности  в точке
в точке  .
.
Решение. Запишем уравнение поверхности в виде  . Тогда
. Тогда  . Вычисляем частные производные от этой функции в точке
. Вычисляем частные производные от этой функции в точке 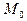 :
:
 ,
, 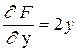 ,
,  ;
;
 ,
,  ,
, 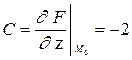 .
.
Искомое уравнение касательной плоскости запишется в виде  или
или  .
.
Нормаль перпендикулярна касательной плоскости. Следовательно, нормальный вектор  =(−5;3;−1) касательной плоскости будет направляющим вектором нормали. Канонические уравнения нормали будут иметь вид
=(−5;3;−1) касательной плоскости будет направляющим вектором нормали. Канонические уравнения нормали будут иметь вид
 .
.
Ответ:  – уравнение касательной плоскости,
– уравнение касательной плоскости,
 – уравнения нормали.
– уравнения нормали.
К задачам 231 – 240.
Для нахождения экстремумов функции z = f (x,y) сначала нужно найти стационарные точки этой функции, в которых частные производные функции z = f (x,y) равны нулю. Для этого нужно решить систему уравнений:
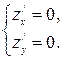 (1)
(1)
Условие (1) является необходимым условием экстремума, но оно не является достаточным, т.е. в стационарной точке экстремума может и не быть.
Рассмотрим достаточное условие экстремума. Пусть точка M0 – стационарная точка функции z=f (x,y), которая имеет непрерывные частные производные второго порядка на некоторой окрестности точки M0,
 и
и
 – определитель второго порядка.
– определитель второго порядка.
Если D>0, то экстремум в точке M0 есть, при этом M0 – точка минимума при A >0 и M0 – точка максимума при A <0. Если D<0, то экстремума в точке M0 нет.
При D=0 требуются дополнительные исследования функции в окрестности точки M0, мы не будем рассматривать этот случай.
Пример. Найти экстремумы функции z = x 3 + y 3 – 6 xy.
Решение. Найдем стационарные точки данной функции. Для этого находим частные производные функции z = x 3 + y 3 – 6 xy, приравниваем их к нулю и решаем полученную систему уравнений.
 .
.

Получили две стационарные точки: М 1(0; 0), М 2(2; 2). Выясним, есть ли в этих точках экстремумы. Находим частные производные второго порядка.
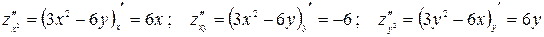 .
.
1) Вычислим значения частных производных второго порядка в точке М1:
 .
.
Находим определитель  :
:
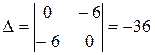 .
.
Поскольку D < 0, то экстремума в точке М 1 нет.
2) Вычислим значения частных производных второго порядка в точке М 2.
 .
.
Определитель 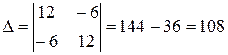 .
.
Поскольку D > 0 и А > 0, то М 2 – точка минимума.
z min = z (2, 2) = 8 + 8 – 24 = − 8.
Ответ: z min = z (2, 2) = − 8.
К задачам 241 − 250.
Градиентом функции  в некоторой точке
в некоторой точке 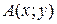 называется вектор, координаты которого равны соответствующим частным производным данной функции:
называется вектор, координаты которого равны соответствующим частным производным данной функции:
 .
.
Пусть из данной точки 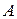 проведен луч
проведен луч  , параллельный некоторому вектору
, параллельный некоторому вектору 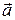 . Производной функции
. Производной функции  по направлению этого луча называется скорость изменения функции в заданном направлении, то есть
по направлению этого луча называется скорость изменения функции в заданном направлении, то есть
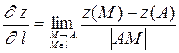 .
.
Если луч  образует с осями
образует с осями  и
и 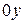 углы
углы  и
и  соответственно, то
соответственно, то  и
и  являются координатами единичного вектора
являются координатами единичного вектора  , параллельного
, параллельного  , и производную по направлению можно вычислить по формуле
, и производную по направлению можно вычислить по формуле
 .
.
При этом, если направление определяется вектором  , то
, то  и значит
и значит
 .
.
Линия уровня функции z = f(x, y) – это линия, определяемая уравнением f(x, y) = С, где С Î R.
Пример. Дана функция  и две точки
и две точки 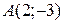 и
и  . Найти градиент функции
. Найти градиент функции  в точке
в точке 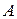 и производную в точке
и производную в точке 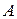 в направлении вектора
в направлении вектора  .
.
Решение. Вычислим частные производные в точке  :
:
 ;
;
 .
.
Значит,  .
.
Найдем направляющие косинусы:
 ;
;
 .
.
Вычисляем по формуле производную в заданном направлении:
 .
.
Ответ:  ;
;  .
.
К задачам 251 – 280.
Операционное исчисление (преобразование Лапласа)
В операционном исчислении функции  действительной переменной
действительной переменной  ставится в соответствие функция
ставится в соответствие функция 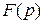 комплексной переменной
комплексной переменной 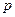 .
.
Функция  называется оригиналом,
называется оригиналом, 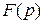 – изображением, что обоз-начают
– изображением, что обоз-начают
 или
или 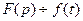 .
.
Соответствие, определяемое формулой
 ,
,
называется преобразованием Лапласа.
Рассмотрим некоторые свойства преобразования Лапласа.
1) Линейность:
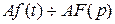 ,
,
 .
.
Постоянный множитель  сохраняется при нахождении изображения.
сохраняется при нахождении изображения.
Изображение суммы равно сумме изображений.
2) Теорема смещения:
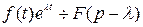 .
.
При умножении оригинала на показательную функцию  в изображении надо из аргумента
в изображении надо из аргумента  вычесть число
вычесть число  .
.
3) Дифференцирование изображения:
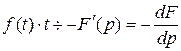 .
.
При умножении оригинала f (t) на  надо изображение
надо изображение 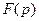 продиффе-ренцировать и производную умножить на (-1).
продиффе-ренцировать и производную умножить на (-1).
4) Изображение производных:
 ,
,
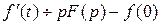 ,
,
 .
.
Таблица изображений
 , ,
| 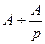 , ,
|  , ,
|
 , ,
|
 , ,
|
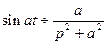 , ,
|
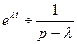 , ,
|  , ,
|  . .
|
Здесь  , гиперболические функции
, гиперболические функции
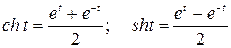 .
.
Примеры.
1. Найти изображение данного оригинала.
1)  .
.
Использовали свойство линейности и формулы
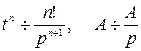 .
.
2)  .
.
3)  , так как
, так как  .
.
По теореме смещения в изображении функции 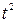 из аргумента
из аргумента  вычли
вычли  , в изображении
, в изображении  из
из  вычли
вычли  .
.
4) 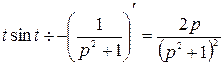 , так как
, так как 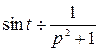 .
.
По свойству дифференцирования изображения оригинал  умножили на
умножили на  , а от изображения
, а от изображения  нашли производную и умножили на – 1.
нашли производную и умножили на – 1.
2. Найти оригинал по заданному изображению.
1)  .
.
Использованы формулы:
 .
.
2) 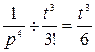 .
.
Если в изображении 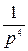 из
из  вычесть
вычесть  , то по теореме смещения оригинал
, то по теореме смещения оригинал  надо умножить на
надо умножить на  :
:
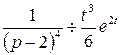 ,
,  .
.
3)  .
.
4) 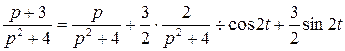 .
.
5)  .
.
6) 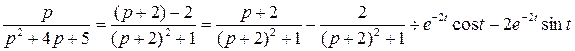 .
.
Чтобы найти оригинал, соответствующий правильной рациональной дроби, надо представить ее в виде суммы простейших дробей, разложив знаменатель на множители.
7) 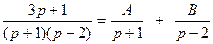 .
.
Линейному множителю  знаменателя соответствует простейшая дробь первого рода
знаменателя соответствует простейшая дробь первого рода  .
.
Находим числа  . Для этого складываем дроби в правой части и приравниваем числители.
. Для этого складываем дроби в правой части и приравниваем числители.
 .
.
Придаем значения  , обращающие одну из скобок в нуль:
, обращающие одну из скобок в нуль:

 .
.
8) 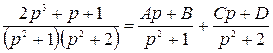 .
.
Квадратному трехчлену с комплексными корнями знаменателя соответствует простейшая дробь 2-го рода, у которой числитель есть линейная функция с неизвестными коэффициентами.
 .
.
Для нахождения  приравниваем коэффициенты при одинаковых степенях р в левой части и в правой. При
приравниваем коэффициенты при одинаковых степенях р в левой части и в правой. При 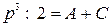 , при
, при  , при
, при 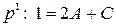 , при
, при  . Получим систему уравнений, решая которую, находим коэффициенты
. Получим систему уравнений, решая которую, находим коэффициенты  .
.
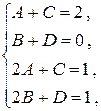

Подставляя найденные коэффициенты и используя таблицу изображений, находим оригинал для данного изображения:

 .
.
9)  .
.
Множителю  соответствуют две простейшие дроби первого рода со знаменателями
соответствуют две простейшие дроби первого рода со знаменателями  и
и  .
.
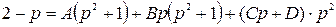 .
.
Приравниваем коэффициенты при одинаковых степенях р. При  , при
, при  , при
, при  , при
, при  . Решая полученную систему, находим, что
. Решая полученную систему, находим, что  ,
,  ,
,  ,
,  . Используя таблицу изображений, получим, что
. Используя таблицу изображений, получим, что
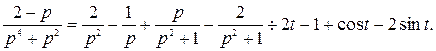
Не нашли, что искали? Воспользуйтесь поиском: