Статистические критерии и их характеристики

Во многих случаях требуется на основе опытных данных, например, выборки, проверить то или иное предположение. Например: «верно ли, что два набора данных получены из одного и того же распределения?», «верно ли, что данная выборка получена из нормального распределения?» и т.д. Рассмотрение таких задач приводит в строгой математической постановке к статистической гипотезе.

В обычном языке слово "гипотеза" означает предположение, которое вызывает сомнение. В математической статистике термин " гипотеза" означает предположение, которое не только вызывает сомнения, но и которое мы собираемся в данный момент проверить.

Статистической гипотезой называется любое предположение относительно параметров или вида (или свойствах) распределения генеральной совокупности, которое мы хотим проверить по имеющимся данным.

Различают простые и сложные (составные) гипотезы. Простая гипотеза однозначно фиксирует распределение вероятностей генеральной совокупности. Гипотеза называется сложной, если она указывает не одно, а несколько распределений (семейство распределений). Обычно это семейство распределений, обладающих определенным свойством.

Будем обозначать выдвигаемую (проверяемую) гипотезу (обычно ее называют основной или нулевой гипотезой) как . Наша задача тогда состоит в том, чтобы сформулировать такое правило, которое позволяло бы по результатам статистических измерений принять или отклонить эту гипотезу.

Правило (процедура), по которому принимается или отклоняется гипотеза , называется критерием согласия (статистическим критерием, критерием значимости) проверки гипотезы . При этом, строго говоря, нельзя доказать гипотезу, ее можно только опровергнуть.

Рассмотрим примеры математических формулировок наиболее распространенных статистических гипотез.

1. Гипотеза о виде распределения. Пусть произведено независимых наблюдений над случайной величиной с неизвестной функцией распределения . Тогда в качестве гипотезы может быть гипотеза вида 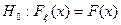, где функция полностью определена (это простая гипотеза), либо вида F, где F – заданное семейство функций распределения, например вида F: , где – параметр распределения (это сложная гипотеза).

2. Параметрическая гипотеза. , где – неизвестный параметр распределения генеральной совокупности, а – некоторая константа.

Общий метод построения критерия согласия состоит в следующем. Пусть о распределении выборки сформулирована некоторая гипотеза, тогда необходимо найти такую статистику , характеризующую отклонение эмпирических данных от (соответствующих гипотезе ) гипотетических значений, распределение которой в случае справедливости можно было бы определить (точно или приближенно). В частности, если гипотеза сложная, то распределение должно быть одним и тем же для всех простых гипотез, составляющих .

Предположим, что такая статистика и ее распределение при гипотезе найдены. Обозначим через T 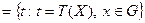множество допустимых значений статистики критерия согласия. Обозначим через T множество нетипичных значений (критическая область ) при гипотезе и пусть вероятность осуществления события в случае справедливости гипотезы удовлетворяет условию:

.

Число 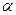называют уровнем значимости критерия и его можно считать вероятностью ложного отвержения гипотезы , когда на самом деле она верна. Фактически 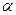- это наибольшее значение вероятности, несовместимое с признанием случайности экспериментально вычисленного значения статистики критерия. В конкретных задачах величину 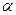выбирают равной 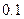, , и т.д.

Таким образом, критерий проверки гипотезы можно сформулировать так. Пусть 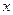– наблюдавшаяся реализация случайной величины , а 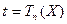– соответствующее значение статистики . Если 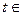, то гипотезу следует отвергнуть. В противном случае считаем, что данные не противоречат гипотезе . Отметим, что факт T не является доказательством истинности гипотезы. Он лишь показывает, что согласие опытных данных и теоретических очень хорошее (на уровне значимости ).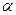

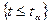В описанной методике называют статистикой критерия, а дополнительную область T - доверительной областью статистики Очевидно, что область должна включать в себя все маловероятные при гипотезе значения статистики критерия. Обычно используют области вида (для неотрицательных статистик ) или , или .

Для проверки гипотезы можно построить различные критерии согласия, основываясь на разных статистиках . Поэтому, чтобы выбрать в той или иной ситуации какой-нибудь критерий, надо уметь сравнивать между собой эти критерии. Это можно проделать, если исследовать поведение критерия при тех или иных отклонениях от основной гипотезы. Для этого вводится понятие альтернативной гипотезы и мощности критерия.

Любое распределение, которое может встретиться нам в случае нарушения основной гипотезы , называют альтернативным распределением или альтернативой. Совокупность всех альтернативных распределений называют альтернативной гипотезой и обозначают символом .

Пусть для проверяемой гипотезы построен некоторый критерий с уровнем значимости 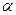, основанный на статистике , и пусть – соответствующая критическая область. Тогда величину , равную вероятности попадания значения статистики критерия в критическую область, когда верна альтернатива , называют мощностью критерия.

При проверке гипотезы возможны ошибочные заключения двух типов: ошибки первого и второго рода.

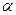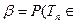Ошибка первого рода – это вероятность отвержения гипотезы , когда она на самом деле верна, т.е. она совпадает с уровнем значимости . Ошибка второго рода – это вероятность неотвержения (принятия) гипотезы , когда на самом деле она не верна. Обозначим эту ошибку символом . Тогда T . Отсюда следует, что . Это равенство выполняется только для простых гипотез. Отметим, что критерий согласия тем мощнее (эффективнее), чем больше мощность критерия при альтернативах. Значение характеризует вероятность принятия правильного решения в ситуации, когда гипотеза ложна. Желательным свойством критерия является свойство несмещенности, т.е. когда одновременно с условием должно выполняться условие . Это означает, что если гипотеза неверна, то она должна отвергаться с вероятностью, большей 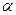. Вычисление мощности критерия сложная задача, так как нужно знать распределение статистики альтернативной гипотезы, поэтому удается найти не во всех случаях.

На практике очень часто требуется одновременно уменьшить ошибки 1-го и 2-го рода, т.е. 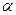и , но, как правило, уменьшение одной из них влечет увеличение другой. В большинстве случаев одновременное уменьшение 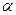и заключается в увеличении объема выборки . В том случае, если – сложная гипотеза, вероятность ошибки первого рода практически сложно определить, но если рассматривать как множество простых гипотез, то для каждой из них можно вычислить вероятность попадания в критическую область. Тогда максимальная из этих вероятностей и принимается за .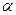

Не нашли, что искали? Воспользуйтесь поиском: