
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Критерий согласия (хи-квадрат) К. Пирсона
На практике вычисление статистики  (в критерии Колмогорова) – трудоемкая задача, поэтому часто применяют другой критерий, называемый критерием
(в критерии Колмогорова) – трудоемкая задача, поэтому часто применяют другой критерий, называемый критерием  (хи-квадрат). Его можно использовать для любых распределений, в том числе и многомерных. Критерий Пирсона основан на сравнении эмпирической функции (гистограммы) распределения с гипотетической функцией (плотностью) распределения, выбранной в качестве основной гипотезы, т.е.
(хи-квадрат). Его можно использовать для любых распределений, в том числе и многомерных. Критерий Пирсона основан на сравнении эмпирической функции (гистограммы) распределения с гипотетической функцией (плотностью) распределения, выбранной в качестве основной гипотезы, т.е. 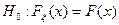 , где
, где 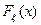 - функция распределения генеральной совокупности, которая нам не известна; а
- функция распределения генеральной совокупности, которая нам не известна; а  - гипотетическая функция распределения, которая выбирается произвольно.
- гипотетическая функция распределения, которая выбирается произвольно.
Критерий строится следующим образом. Полученную выборку (если предполагать, что она получена из непрерывного распределения) предварительно группируют, т.е. переходят к частотному представлению данных. Для этого всю числовую ось необходимо разбить на  интервалов группировки:
интервалов группировки:  .
.
Обозначим эти интервалы как:  ,
, 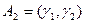 , …,
, …,  . Далее, по известной функции распределения
. Далее, по известной функции распределения  вычисляем вероятности
вычисляем вероятности 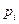 попадания значений выборки в указанные интервалы группировки
попадания значений выборки в указанные интервалы группировки 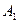 ,
, 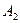 , …,
, …,  :
:
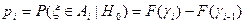 ,
, 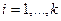 ,
,
причем  .
.
Обозначим через 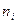 число тех
число тех 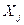 из выборки
из выборки  (
(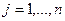 ), которые удовлетворяют условию:
), которые удовлетворяют условию:  . Тогда при справедливости основной гипотезы
. Тогда при справедливости основной гипотезы  случайные величины (частоты)
случайные величины (частоты)  ,
, 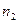 , …,
, …,  имеют полиномиальное распределение с числом испытаний
имеют полиномиальное распределение с числом испытаний  и вероятностями исходов
и вероятностями исходов 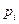 (
(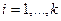 ). Тогда
). Тогда
 .
.
Тем самым первоначальная задача сведена к проверке гипотезы о том, что частоты  ,
, 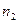 , …,
, …,  имеют полиномиальное распределение. В этом случае частоты
имеют полиномиальное распределение. В этом случае частоты 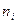 должны быть близки к среднему значению
должны быть близки к среднему значению 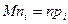 ,
, 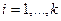 . Обще отклонение всех частот можно измерять разными способами. Чаще всего в качестве меры отклонения используют статистику
. Обще отклонение всех частот можно измерять разными способами. Чаще всего в качестве меры отклонения используют статистику 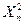 , введенную К. Пирсоном:
, введенную К. Пирсоном:
 .
.
Величина 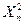 случайна и называется статистикой хи-квадрат Пирсона. Пирсон доказал, что она обладает важным свойством: при
случайна и называется статистикой хи-квадрат Пирсона. Пирсон доказал, что она обладает важным свойством: при  случайная величина
случайная величина 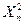 при справедливости основной гипотезы асимптотически подчиняется распределению
при справедливости основной гипотезы асимптотически подчиняется распределению  с
с 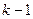 степенями свободы (здесь
степенями свободы (здесь  это количество интервалов группировки либо это число исходов в одном испытании при рассмотрении дискретных распределений).
это количество интервалов группировки либо это число исходов в одном испытании при рассмотрении дискретных распределений).
С помощью этого результата введем следующий критерий проверки гипотезы  . Зададим уровень значимости
. Зададим уровень значимости  , выберем величины
, выберем величины  ,
, 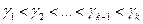 и найдем по ним вероятности
и найдем по ним вероятности 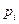 . Фактически, гипотеза
. Фактически, гипотеза  выглядит так:
выглядит так: 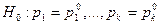 , где
, где  – это гипотетические вероятности попадания в
– это гипотетические вероятности попадания в 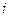 –ый интервал группировки, которые либо даны заранее, либо вычисляются на основе распределения
–ый интервал группировки, которые либо даны заранее, либо вычисляются на основе распределения  . Гипотеза
. Гипотеза  здесь является простой, так как все параметры распределения
здесь является простой, так как все параметры распределения  известны. Границу критической области
известны. Границу критической области  критерия Пирсона для проверки гипотезы
критерия Пирсона для проверки гипотезы  находим из условия, что
находим из условия, что  . Тогда, так как
. Тогда, так как 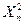 имеет распределение
имеет распределение  с
с 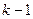 степенями свободы, то в качестве критического значения критерия берем величину
степенями свободы, то в качестве критического значения критерия берем величину 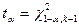 , т.е. квантиль распределения
, т.е. квантиль распределения  на уровне
на уровне  . Таким образом, если
. Таким образом, если  , то гипотеза
, то гипотеза  о виде распределения отвергается в пользу других распределений. Асимптотический характер распределения
о виде распределения отвергается в пользу других распределений. Асимптотический характер распределения 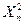 требует осторожности при практическом использовании этого критерия. На него можно полагаться, только если все
требует осторожности при практическом использовании этого критерия. На него можно полагаться, только если все 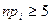 , при этом считаем, что
, при этом считаем, что 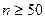 . Чтобы соблюсти эти требования, на практике порой приходиться объединять несколько интервалов группировки, т.е. переходить к полиномиальной схеме с меньшим числом
. Чтобы соблюсти эти требования, на практике порой приходиться объединять несколько интервалов группировки, т.е. переходить к полиномиальной схеме с меньшим числом  . Укажем следующие правила выбора
. Укажем следующие правила выбора  :
:
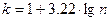 или
или 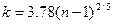 при
при  .
.
Можно рекомендовать еще одно простое правило: нужно выбирать как можно большее  , но не превышающее
, но не превышающее 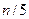 .
.
Пример. При  бросаниях монеты "герб" выпал 2048 раз. Требуется проверить гипотезу
бросаниях монеты "герб" выпал 2048 раз. Требуется проверить гипотезу  о том, что монета была симметричной, т.е. что вероятности выпадения "герба" и "цифры" равны соответственно
о том, что монета была симметричной, т.е. что вероятности выпадения "герба" и "цифры" равны соответственно 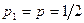 и
и  .
.
Здесь число исходов 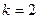 . Проверяемая гипотеза
. Проверяемая гипотеза  :
:  , т.е. гипотетическое распределение является биномиальным распределением с параметром
, т.е. гипотетическое распределение является биномиальным распределением с параметром 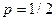 . Тогда
. Тогда  ,
,  . Вычисляем статистику критерия:
. Вычисляем статистику критерия:
 .
.
Возьмем уровень значимости  , тогда число степеней свободы равно
, тогда число степеней свободы равно 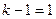 . По таблицам распределения
. По таблицам распределения  находим квантиль
находим квантиль  . Сравниваем полученное значение
. Сравниваем полученное значение 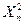 с табличной величиной
с табличной величиной 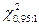 . Так как
. Так как  , то гипотеза
, то гипотеза  не отвергается, т.е. монету можно считать симметричной.
не отвергается, т.е. монету можно считать симметричной.
Критерий согласия хи-квадрат Фишера при неизвестных параметрах распределения (для сложной гипотезы)
Изложенный выше критерий Пирсона применим в том случае, когда гипотеза  является простой, т.е. проверяемое распределение
является простой, т.е. проверяемое распределение  полностью определено. Однако чаще встречаются случаи, когда известен лишь тип закона распределения (например, нормальное), но неизвестны некоторые его параметры
полностью определено. Однако чаще встречаются случаи, когда известен лишь тип закона распределения (например, нормальное), но неизвестны некоторые его параметры  . и гипотеза
. и гипотеза  состоит в проверке того, что
состоит в проверке того, что  . Для проверки таких сложных гипотез может быть использована модификация критерия Пирсона.
. Для проверки таких сложных гипотез может быть использована модификация критерия Пирсона.
Пусть исходные данные (выборка  ) сгруппированы и
) сгруппированы и  ,
, 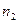 , …,
, …,  – частоты наблюдений, попавших в интервалы группировки
– частоты наблюдений, попавших в интервалы группировки  ,
, 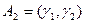 , …,
, …,  . Пусть вероятности попадания в эти интервалы группировки (вероятности исходов) при гипотезе
. Пусть вероятности попадания в эти интервалы группировки (вероятности исходов) при гипотезе  известны с точностью до параметра
известны с точностью до параметра  . Тогда эти вероятности являются функциями от
. Тогда эти вероятности являются функциями от  :
:  , причем
, причем 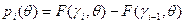 . Будем предполагать, что
. Будем предполагать, что 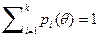 для всякого
для всякого  . Тогда при
. Тогда при  статистика
статистика
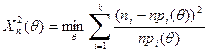
асимптотически распределена по закону хи-квадрат  с
с 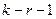 степенями свободы (здесь
степенями свободы (здесь  - это число неизвестных параметров гипотетического распределения
- это число неизвестных параметров гипотетического распределения  ). Существует много вариантов теоремы Фишера. Например, такое же, как выше, предельное распределение имеет статистика
). Существует много вариантов теоремы Фишера. Например, такое же, как выше, предельное распределение имеет статистика
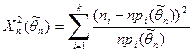 ,
,
где  – точечная оценка максимального правдоподобия для параметра
– точечная оценка максимального правдоподобия для параметра  , найденная по частотам
, найденная по частотам  ,
, 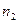 , …,
, …,  , тогда статистику
, тогда статистику  можно однозначно найти. Статистика
можно однозначно найти. Статистика  называется статистикой хи-квадрат Фишера для сложной гипотезы.
называется статистикой хи-квадрат Фишера для сложной гипотезы.
Проверка гипотезы  осуществляется так: на уровне значимости
осуществляется так: на уровне значимости  гипотеза
гипотеза  отвергается, если
отвергается, если 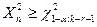 .
.
Например, пусть проверяется гипотеза о нормальности выборки, причем параметры распределения 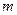 и
и  неизвестны. Тогда, в качестве оценок этих параметров берем статистики
неизвестны. Тогда, в качестве оценок этих параметров берем статистики  и
и 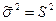 . Далее, находим вероятности попадания в интервалы группировки:
. Далее, находим вероятности попадания в интервалы группировки: 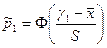 ,
,  , …,
, …,  . После этого вычисляем значение статистики хи-квадрат Фишера и сравниваем его с соответствующим значением квантили распределения хи-квадрат.
. После этого вычисляем значение статистики хи-квадрат Фишера и сравниваем его с соответствующим значением квантили распределения хи-квадрат.
Не нашли, что искали? Воспользуйтесь поиском: