
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Результаты измерений.
Приборы и модули.
Электронный осциллограф, генератор звуковых частот, универсальный лабораторный стенд, модули № 1, 2, 6.
 |
Рис.1. Схема для исследования дифференцирующей цепи.
Для интегрирующей цепи в схеме меняются местами конденсатор и резистор.
Рабочие формулы.
 , (1)
, (1)
где К – модуль коэф. передачи,
Uвх –напряжение входного сигнала
Uвых –напряжение выходного сигнала
 , (2)
, (2)
где 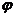 - сдвиг фазы между выходным и входным сигналами,
- сдвиг фазы между выходным и входным сигналами,
 - временной сдвиг выходного сигнала по отношению ко входному,
- временной сдвиг выходного сигнала по отношению ко входному,
Т – период сигнала.
 (3)
(3)
где  - постоянная времени,
- постоянная времени,
 - граничная частота.
- граничная частота.
Результаты измерений.
В ходе выполнения лабораторной работы к универсальному лабораторному стенду подключались генератор звуковых частот, модули № 1, 2, которые при помощи соединительных проводов образовывали дифференцирующую либо интегрирующую цепочки. С генератора звуковых частот сначала на вход, потом на выход цепи подавался сигнал определенной частоты, реакция цепи регистрировалась с помощью осциллографа. На этих же частотах измерялся период сигнала и временной сдвиг выходного сигнала по отношению ко входному, используя осциллограф в режиме внешней синхронизации. С помощью формул (1) и (2) рассчитывались модуль коэф. передачи и сдвиг фазы между выходным и входным сигналами.
Полученные экспериментальные и расчетные данные представлены в таблице 1.
Таблица 1 – Результаты измерений и расчетов для дифференцирующей либо интегрирующей RС- цепи.
| Дифференцирующая цепочка | |||||||
| f, кГц | 0,5 | 1,5 | |||||
| Uвх/В | 20,0 | 20,0 | 20,0 | 20,0 | 20,0 | 20,0 | 20,0 |
| Uвых.В | 9,6 | 12,4 | 14,8 | 17,0 | 18,0 | 19,0 | 19,6 |
| K | 0,48 | 0,62 | 0,74 | 0,85 | 0,90 | 0,95 | 0,98 |
| T, мс | 2,0 | 0,95 | 0,64 | 0,46 | 0,24 | 0,114 | 0,06 |
| t, мс | 0,4 | 0,16 | 0,08 | 0,05 | 0,015 | 0,003 | 0,001 |
| φ, рад | 1,3 | 1,0 | 0,8 | 0,7 | 0,4 | 0,2 | 0,1 |
| Интегрирующая цепочка | |||||||
| Uвх.В | 20,0 | 20,0 | 20,0 | 20,0 | 20,0 | 20,0 | 20,0 |
| Uвых.В | 17,0 | 13,0 | 10,0 | 8,0 | 5,0 | 2,4 | 1,1 |
| K | 0,85 | 0,65 | 0,50 | 0,40 | 0,25 | 0,12 | 0,055 |
| T, мс | 2,0 | 1,0 | 0,7 | 0,5 | 0,25 | 0,1 | 0,06 |
| t, мс | -0,12 | -0,11 | -0,11 | -0,10 | -0,06 | -0,02 | -0,01 |
| φ, рад | -0,38 | -0,69 | -1 | -1,25 | -1,5 | -1,54 | -1,55 |
По рассчитанным значениям модуля коэффициента передачи и сдвига фаз построены графики зависимости этих величин от частоты сигнала  и
и  для дифференцирующей и интегрирующей цепочек. К графикам сделаны соответствующие выводы и рассчитаны постоянные времени для каждого. Рассчитаем
для дифференцирующей и интегрирующей цепочек. К графикам сделаны соответствующие выводы и рассчитаны постоянные времени для каждого. Рассчитаем  по формуле
по формуле  . Значения постоянной времени различны за счет приборных погрешностей и округления.
. Значения постоянной времени различны за счет приборных погрешностей и округления.

Рис.2. График зависимости модуля коэффициента передачи от частоты сигнала  для дифференцирующей цепочки.
для дифференцирующей цепочки.
Для дифференцирующей цепи 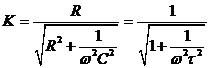 , когда реактивное сопротивление становится равным активному К принимает значение
, когда реактивное сопротивление становится равным активному К принимает значение  , значение граничной частоты будет лежать на пересечении прямой
, значение граничной частоты будет лежать на пересечении прямой  с графиком
с графиком  и постоянная времени определяется по формуле (3).
и постоянная времени определяется по формуле (3).

Зависимость, коэффициента передачи от частоты можно объяснить, рассматривая дифференцирующую цепь как делитель входного напряжения. Одно плечо делителя - частотно-зависимое реактивное сопротивление конденсатора, другое – активное сопротивление R. С увеличением частоты уменьшается сопротивление конденсатора и падение напряжения на нем UC. Поскольку U1 = UR + UC (U1 - входное напряжение), то уменьшение UC сопровождается возрастанием (на выходе RС -цепи).

Рис.3. График зависимости сдвига фаз от частоты сигнала  для дифференцирующей цепочки.
для дифференцирующей цепочки.
Для дифференцирующей цепи  , когда реактивное сопротивление становится равным активному
, когда реактивное сопротивление становится равным активному 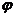 принимает значение
принимает значение  , и значение граничной частоты будет лежать на пересечении прямой
, и значение граничной частоты будет лежать на пересечении прямой  с графиком
с графиком  и постоянная времени определяется по формуле (3).
и постоянная времени определяется по формуле (3).

Фазовый сдвиг объясняется наличием в цепи реактивного элемента - конденсатора. Так как делителем напряжения является резистор, то  - это коэффициент передачи делителя, и фазовый сдвиг определяется его аргументом
- это коэффициент передачи делителя, и фазовый сдвиг определяется его аргументом  , где
, где  является частотно-зависимой величиной. Фазовый сдвиг положительный, так как напряжение на резисторе отстает от напряжения на конденсаторе, следовательно выходной сигнал опережает входной (максимум на
является частотно-зависимой величиной. Фазовый сдвиг положительный, так как напряжение на резисторе отстает от напряжения на конденсаторе, следовательно выходной сигнал опережает входной (максимум на  ).
).
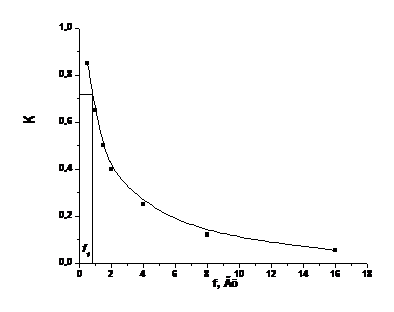
Рис.4. График зависимости модуля коэффициента передачи от частоты сигнала  для интегрирующей цепочки.
для интегрирующей цепочки.
Для интегрирующей цепи  , когда реактивное сопротивление становится равным активному К принимает значение
, когда реактивное сопротивление становится равным активному К принимает значение  , значение граничной частоты будет лежать на пересечении прямой
, значение граничной частоты будет лежать на пересечении прямой  с графиком
с графиком  и постоянная времени определяется по формуле (3).
и постоянная времени определяется по формуле (3).

С увеличением частоты уменьшается сопротивление конденсатора и падение напряжения на нем UC. Поскольку U1 = UR + UC (U1 - входное напряжение), то уменьшение UC сопровождается спадом на выходе RС -цепи.

Рис.5. График зависимости сдвига фаз от частоты сигнала  для интегрирующей цепочки.
для интегрирующей цепочки.
Для интегрирующей цепи  , когда реактивное сопротивление становится равным активному
, когда реактивное сопротивление становится равным активному 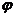 принимает значение
принимает значение 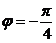 , и значение граничной частоты будет лежать на пересечении прямой
, и значение граничной частоты будет лежать на пересечении прямой 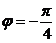 с графиком
с графиком  и постоянная времени определяется по формуле (3).
и постоянная времени определяется по формуле (3).

Фазовый сдвиг объясняется наличием в цепи реактивного элемента - конденсатора. Так как делителем напряжения в данном случае является конденсатор  - это коэффициент передачи делителя, то фазовый сдвиг определяется его аргументом. Фазовый сдвиг отрицательный, так как напряжение на резисторе опережает напряжение на конденсаторе, следовательно выходной сигнал отстает от входного (максимум на
- это коэффициент передачи делителя, то фазовый сдвиг определяется его аргументом. Фазовый сдвиг отрицательный, так как напряжение на резисторе опережает напряжение на конденсаторе, следовательно выходной сигнал отстает от входного (максимум на  ).
).
| <== предыдущая лекция | | | следующая лекция ==> |
| | |
Не нашли, что искали? Воспользуйтесь поиском: