Спектр видеоимпульса прямоугольной формы

Представим видеоимпульс в виде суммы двух функций включения:

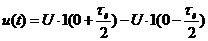(2.7)

Рассматриваемый сигнал показан на рис. 2.3.

Рис. 2.3. Одиночный прямоугольный видеоимпульс

В выражении (2.7) первый член есть функция включения с запаздыванием на время , что учитывается множителем :

.

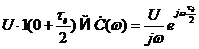Второй член есть функция включения с опережением 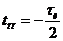, что учитывается множителем :

.

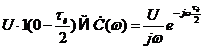Тогда спектр видеоимпульса определяется выражением

.

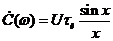, (2.8)

где .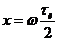

Из выражения (2.8) следует, что спектр при выбранном в середине импульса начале отсчета времени получился вещественным. Его график определяется законом изменения функции , которая при х = 0 имеет максимальное значение, равное единице. С ростом частоты эта функция немонотонно убывает, проходя через ноль при , где k = 1, 2, 3…, то есть на частотах

; ; .

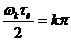График изменения спектральной плотности (2.8) показан на рис. 2.4,а пунктиром. Сплошной линией показан модуль спектральной плотности, то есть амплитудно-частотный спектр. При f = 0 спектральная плотность равна площади импульса 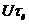. Чем больше эта величина, тем больше энергия сигнала и тем больше его спектральная плотность.

а)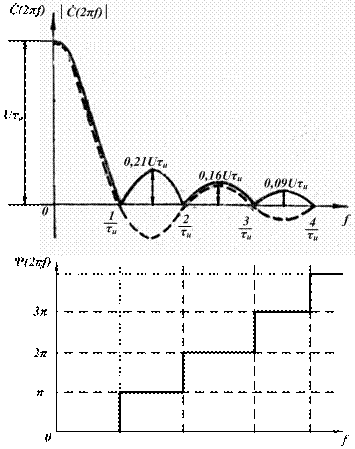
б)

Рис. 2.4. Спектр прямоугольного видеоимпульса: а – АЧС, б – ФЧС

На рис. 2.4,б показан фазо-частотный спектр. При частотах значение функции (2.8) меняет знак на противоположный. Функцию (2.8) можно представить в следующем виде:

, (2.9)

где модуль выражения (2.9) есть АЧС, а – ФЧС.

Действительно, представляя

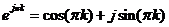при k = 1, 2, 3,…,

имеет место тождество

. (2.10)

Для оценки влияния длительности импульса на его спектр сопоставим два спектра импульсов различной длительности, но одинаковой площади 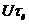. Соответствующие АЧС показаны на рис. 2.5, где площади импульсов приняты 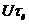= 1 и .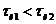

Рис. 2.5. Амплитудно-частотные спектры прямоугольных одиночных видеоимпульсов различной длительности: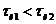

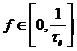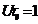Уменьшение длительности импульса влечет расширение АЧС. Часть спектра, ограниченного полосой частот , будем называть главной частью (главным лепестком) АЧС. При уменьшении эта часть спектра расширяясь стремиться к равномерному. При и получаем , то есть спектр становится равномерным. Этот случай соответствует рассмотренному выше спектру дельта-функции.

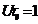При и получаем , то есть в этом случае спектр «сжимается» в одну спектральную линию на частоте f = 0. При имеет место переход от импульса к постоянному напряжению.

Если увеличивать 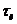, не изменяя величины U, то есть не поддерживать постоянной площадь импульса 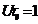, то при спектральная плотность на частоте f = 0 будет стремиться к бесконечности.

2.2. Спектр периодической последовательности прямоугольных
видеоимпульсов

Выражение для определения комплексных амплитуд (1.25) ряда Фурье (1.24) идентично выражению спектральной плотности (1.27):

;

.

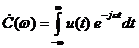По виду они отличаются лишь множителем 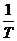и переменной в случае ряда Фурье и 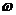для интеграла Фурье. Пределы интегрирования совпадают, так как в обоих случаях они равны интервалу времени, в течение которого функция u(t) отлична от нуля. В связи с этим комплексные амплитуды ряда определяются через спектральную плотность следующим образом:

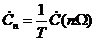, (2.11)

где n = 0, ±1, ±2, ±….

Выражение (2.11) означает, что для вычисления комплексных амплитуд ряда Фурье в случае периодического сигнала достаточно вычислить спектральную плотность одиночного сигнала, из которого образована периодическая последовательность, взять ее значения на частотах и умножить на 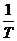. Это выражение позволяет переходить от спектра периодического сигнала к спектру одиночного сигнала, и наоборот.

Рассмотрим спектр периодической последовательности прямоугольных видеоимпульсов, представленных на рис. 2.6. Периодическая последовательность импульсов характеризуется их формой, длительностью 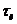, периодом повторения Т (либо частотой ), высотой U. Иногда вводят вторичный параметр – скважность .

Для одиночного прямоугольного видеоимпульса спектральная плотность описывается выражением (2.8):

,

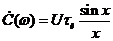где .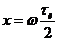

Воспользуемся выражением (2.11) для нахождения комплексных амплитуд спектра периодической последовательности импульсов (1.24):

,

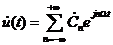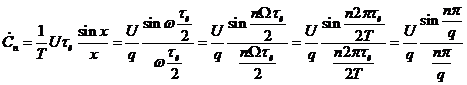. (2.12)

Для построения АЧС и ФЧС необходимо перейти от комплексной формы записи спектра (1.24) к спектру сигнала в виде вещественных амплитудно-фазовых гармоник (1.22):

.

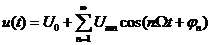Переход должен осуществляться от середины ряда, попарно складывая члены ряда (1.24) с одинаковым номером:

;

,

,

;

,

,

;

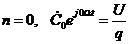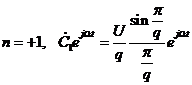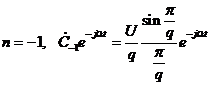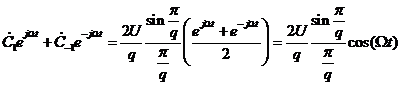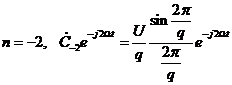и так далее. В результате получим спектр последовательности прямоугольных видеоимпульсов как сумму амплитудно-фазовых гармоник:

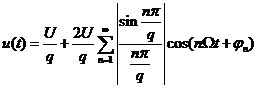. (2.13)

В выражении (2.13) значения в области частот 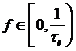. В этой области функция , где , имеет положительные значения. В области частот эта функция имеет отрицательные значения (см. рис. 2.4). Отрицательное значение учитывается начальной фазой во всей области указанных частот. Действительно:

.

В области частот 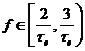функция принимает положительные значения, что соответствует 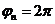, и т.д.

а)

б)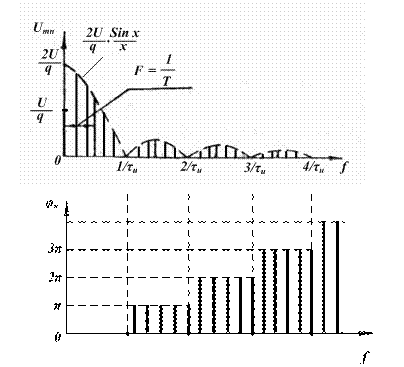
в)

Рис. 2.6: а – последовательность прямоугольных видеоимпульсов; б – АЧС периодической последовательности прямоугольных видеоимпульсов; в – их ФЧС

На рис. 2.6 представлен спектр последовательности прямоугольных видеоимпульсов в предположении, что начало отсчета времени совпадает с серединой импульса. Если это условие не выполняется, то изменяется только фазо-частотный спектр. При запаздывании последовательности импульсов на t₀ (рис. 2.6,а), где t₀ может быть любым, выражение (2.8) примет вид:

. (2.14)

Выражение (2.14) записано на основе сдвига аргумента, при этом

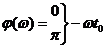, (2.15)

где отброшено четное число .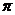

Фазо-частотный спектр в случае запаздывания последовательности импульсов на время t₀ показан на рис. 2.7.

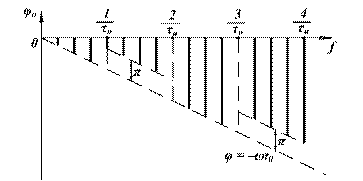
Рис. 2.7. ФЧС в случае запаздывания последовательности видеоимпульсов на время t₀

При изменении длительности импульсов или частоты их повторения, согласно (2.13) будет изменяться их спектральный состав. На рис. 2.8 и 2.9 показаны различные периодические последовательности и соответствующие им амплитудно-частотные спектры. Рис. 2.8 иллюстрирует изменения в спектрах при увеличении длительности импульсов и неизменной частоте их повторения. В этом случае происходит «сжатие» спектра: основные гармонические составляющие в области главного лепестка при увеличении 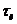смещаются в область низких частот. Вместе с тем происходит уменьшение числа спектральных составляющих в главном лепестке, но амплитуды их увеличиваются, что означает увеличение энергии импульсов и перераспределение основной части энергии на меньшее количество спектральных составляющих в главном лепестке. Расстояние между спектральными составляющими не изменяется.

а)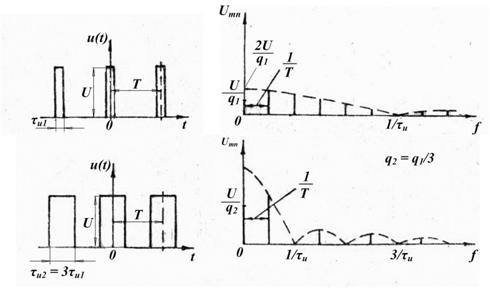
б)

Рис. 2.8. АЧС последовательности прямоугольных видеоимпульсов при неизменной частоте их повторения постоянной величине U и разных длительностях импульсов

Рис. 2.9 иллюстрирует изменения в спектрах при увеличении периода повторения и неизменных U и .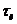

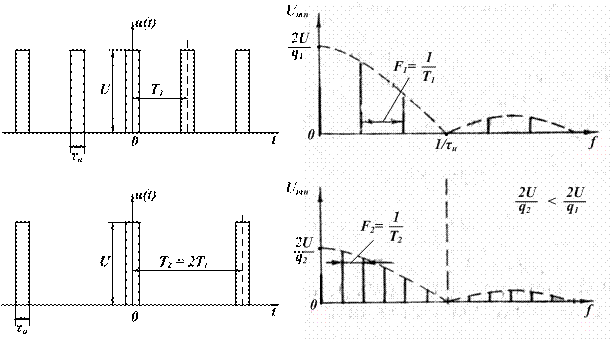
Рис. 2.9. АЧС последовательности прямоугольных видеоимпульсов при неизменных U и 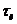и разных периодах повторения

Уменьшение частоты повторения (увеличение периода) приводит к уменьшению расстояния по частотной оси между соседними спектральными линиями. При этом уменьшаются и амплитуды всех составляющих спектра из-за уменьшения энергии в периодической последовательности импульсов. Если устремить 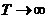, то амплитуды уменьшаются до бесконечно малых величин, а спектр из дискретного вырождается в сплошной. Происходит переход от периодической последовательности к одиночному импульсу.

Не нашли, что искали? Воспользуйтесь поиском: