Частотный модулятор

Частотная модуляция может осуществляться двумя методами: прямым и косвенным.

При прямом методе модулирующее напряжение подается на частотный модулятор (ЧМ), который подключается непосредственно к контуру задающего генератора (автогенератора) и изменяет его частоту.

При косвенном методе вначале осуществляется фазовая модуляция в одном из промежуточных каскадов радиопередатчика с помощью интегрирующей цепочки (ИЦ), затем фазовая модуляция преобразуется в частотную.

Основным достоинством прямого метода является простота схемы и возможность получения большой девиации частоты. Недостатком – невысокая стабильность частоты несущего сигнала. Этот недостаток устраняется в более сложной схеме, реализующей косвенный метод частотной модуляции.

На рис. 3.14 приведена схема частотной модуляции с помощью управляемой емкости p-n-перехода варикапа. Зависимость барьерной емкости p-n-перехода от обратного напряжения приведена на рис. 3.15.

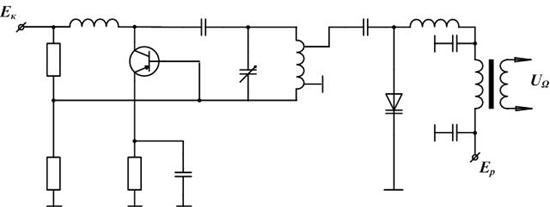
Рис. 3.14. Схема частотного модулятора с управляющей емкостью варикапа

Рис. 3.15. Зависимость барьерной емкости p-n-перехода от обратного напряжения

Варикап – полупроводниковый диод специальной конструкции, емкость которого может изменяться в широких пределах. Емкость p-n-перехода зависит от величины обратного напряжения по следующему закону

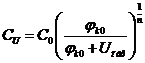, (3.20)

где С₀ – емкость при нулевом напряжении на диоде;

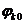– высота потенциального барьера в переходе (десятые доли вольта);

n – коэффициент, зависящий от типа варикапа (n = 2…3).

Схема на рис. 3.14 представляет собой задающий генератор (автогенератор). Поскольку варикап по высокой частоте подключен к колебательному контуру автогенератора, то с подачей модулирующего сигнала 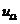будет изменяться и частота генерируемого сигнала.

Фильтры

Фильтры представляют собой пассивные или активные четырехполюсники. Их назначение – в обеспечении заданной полосы частот, в которой АЧХ и ФЧХ соответствуют спектру сигнала сообщения.

Активный фильтр представляет собой четырехполюсник, содержащий пассивные RС-цепи и активные элементы: транзисторы, электронные усилительные лампы или операционные усилители. Такие фильтры обычно не содержат катушек индуктивности по ряду причин:

– катушки индуктивности имеют большие габариты и массу;

– потери в катушках приводят к отклонению расчетных АЧХ и ФЧХ от реальных значений;

– в катушках рассеивается большая мощность;

– рассеиваемые магнитные потоки катушек наводят «паразитные» сигналы в электронных цепях, и для исключения этого негативного явления требуется экранировка катушек;

– в катушках с сердечником проявляется нелинейный эффект, связанный с насыщением сердечника;

Подробно активные фильтры рассмотрены в [11].

Пассивные фильтры выполняются на LC или RC-цепях. Далее рассматриваются пассивные фильтры. Изучение фильтров следует начинать с простейших цепей, так как сложные фильтры, как правило, образуются последовательным соединением простейших цепей-четырехполюсников.

RC-цепи

На рис. 3.16 показаны два способа соединения R и С, представляющие четырехполюсник.

а)	б)

Рис. 3.16. Два способа соединения R и С элементов

Найдем для каждого способа соединения R и С частотный коэффициент передачи, используя для этой цели классический метод (см. п.1.3., выражение (1.20)):

. (3.21)

На основании второго закона Кирхгофа для цепи, приведенной на рис. 3.16, а, имеем

;

;

;

,

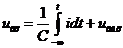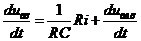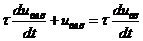где 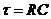– постоянная времени цепи;

u_вых = Ri.

Полученное дифференциальное уравнение запишем в принятом ранее виде (см. п.1.3.):

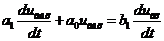, (3.22)

где a₁ = ; a₀ = 1; b₁ = .

Подставляя a₁, a₀, b₁ в (3.21), получим

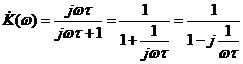. (3.23)

Модуль частотного коэффициента передачи, то есть АЧХ цепи

. (3.24)

Зависимость 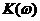показана на рис. 3.17, а

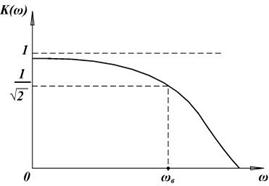
а)	б)

Рис. 3.17. АЧХ RC-цепи: а – для цепи, приведенной на рис. 3.16, а; б – для цепи, приведенной на рис. 3.16, б

Приравнивая выражение (3.24) к 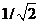, находим значение нижней частоты :

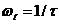. (3.25)

Таким образом, RC-цепь, приведенная на рис. 3.16, а, является фильтром верхних частот. В дальнейшем для различия эту цепь будем называть RC-фильтр верхних частот.

Если в (3.22) 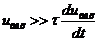, то

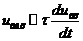. (3.26)

При этом условии цепь на рис. 3.16,а является дифференцирующей. Для прямоугольных импульсных сигналов, поступающих на вход, дифференцирование выполняется при условии

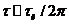, (3.27)

где 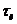– длительность импульса.

При 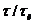< 0,1 цепь полностью дифференцирует входной сигнал.

При 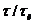> 10 цепь не дифференцирует сигнал и применяется в электронных цепях для разделения путей протекания постоянной и переменной составляющей тока.

Для цепи, приведенной на рис. 3.16, б, аналогичным образом получаем следующее дифференциальное уравнение:

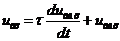. (3.28)

Тогда

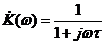, (3.29)

. (3.30)

Вид АЧХ этой цепи показан на рис. 3.17, б. Приравнивая правую часть (3.30) к 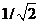, получаем значение верхней частоты:

. (3.31)

Выражение (3.25) и (3.31) совпадают. Таким образом, цепь, приведенная на рис. 3.16, б, является фильтром нижних частот.

Если в (3.28) , то

или . (3.32)

При выполнении данного условия RC-цепь (рис. 3.16, б) является интегрирующей.

Не нашли, что искали? Воспользуйтесь поиском: