
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Поле кругового тока и соленоида
ГЛАВА 5
ЭЛЕКТРОМАГНЕТИЗМ
МАГНИТНОЕ ПОЛЕ ПОСТОЯННОГО ТОКА.
Основные формулы
· Закон Био — Савара — Лапласа
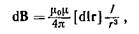
где dB — магнитная индукция поля, создаваемого элементом i водника с током; m — магнитная проницаемость; m0 — магнитная постоянная (m0 =4p · 10 -7 Гн/м); dl — вектор, равный по модулю длине dl проводника и совпадающий по направлению с током (элемент проводника); I — сила тока; r — радиус-вектор, проведенный от середины элемента проводника к точке, магнитная индукция в которой определяется.
Модуль вектора d B выражается формулой
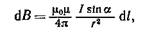
где  a — угол между векторами d l и r.
a — угол между векторами d l и r.
· Магнитная индукция В связана с напряженностью Н магнитного поля (в случае однородной, изотропной среды) соотношением

или в вакууме
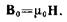
· Магнитная индукция в центре кругового проводника с током

где R — радиус кривизны проводника.
· Магнитная индукция поля, создаваемого бесконечно длинным прямым проводником с током,
 где r — расстояние от оси проводника.
где r — расстояние от оси проводника.
Магнитная индукция поля, создаваемого отрезком проводником

Обозначения ясны из рис. 21.1, а. Вектор индукции В перпендикулярен плоскости чертежа, направлен к нам и поэтому изображен точкой.
При симметричном расположении концов проводника относительно точки, в которой определяется магнитная индукция (рис. 21.1, б),  и, следовательно,
и, следовательно,
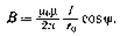
 · Магнитная индукция поля, создаваемого соленоидом в средней его части (или тороида на его оси),
· Магнитная индукция поля, создаваемого соленоидом в средней его части (или тороида на его оси),

где п — число витков, приходящихся на единицу длины соленоида; I — сила тока в одном витке.
· Принцип суперпозиции магнитных полей: магнитная индукция В результирующего поля равна векторной сумме магнитных индукций В 1, В2,..., В n складываемых полей, т. е.

В частном случае наложения двух полей

а модуль магнитной продукции
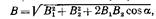
где a — угол между векторами В1 и В2.
 Примеры решения задач
Примеры решения задач
Пример 1. Два параллельных бесконечно длинных провода, по которым текут в одном направлении токи I =60 А, расположены на
расстоянии d= 10 см друг от друга. Определить магнитную индукцию В в точке, отстоящей от одного проводника на расстоянии г1=5 см и от другого — на расстоянии r2 = 12 см.
Решение. Для нахождения магнитной индукции в указанной точке А (рис. 21.2) определим направления векторов индукций В 1 и В 2 по лей, создаваемых каждым проводником в отдельности, и сложим их геометрически, т. е. B=B 1+ B 2. Модуль индукции найдем по теореме косинусов:

Значения индукций Bi и В2 выражаются соответственно через силу тока I и расстояния r1 и r2 от провода до точки, индукцию
в которой мы вычисляем:  Подставляя B1 и В2 в формулу (1) и вынося
Подставляя B1 и В2 в формулу (1) и вынося  за знак корня, получим
за знак корня, получим
 (2)
(2)
Убедимся в том, что правая часть этого равенства дает единицу магнитной индукции (Тл):
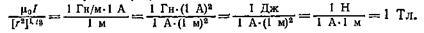
Здесь мы воспользовались определяющей формулой для магнитной индукции (В=Мmак /рп). Откуда следует, что

Вычисляем cosa. Заметим, что a = /_ DAC. Поэтому по теореме косинусов запишем  , где d — расстояние между проводами. Отсюда
, где d — расстояние между проводами. Отсюда

Подставив данные, вычислим значение косинуса: cos a = 0,576.
Подставив в формулу (2) значения m0, I, r1, r2 и cos b, найдем В =286 мкТл.
Пример 2. По двум длинным прямолинейным проводам, находящимся на расстоянии r=5 см друг от друга в воздухе, текут токи I =10 А каждый. Определить магнитную индукцию В поля, создаваемого токами в точке, лежащей посередине между проводами, для случаев: 1) провода параллельны, токи текут в одном направлении (рис. 21.3, а); 2) провода параллельны, токи текут в противоположных направлениях (рис. 21.3, б); 3) провода перпендикулярны, направление токов указано на рис. 21.3, в.
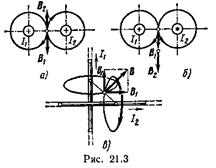 Решение: Результирующая индукция магнитного поля равна векторной сумме: B=B1+B2, где B1 — индукция поля, создаваемого током 1 1; В2 — индукция поля создаваемого током I 2.
Решение: Результирующая индукция магнитного поля равна векторной сумме: B=B1+B2, где B1 — индукция поля, создаваемого током 1 1; В2 — индукция поля создаваемого током I 2.
Если B1 и В2 направлены по одной прямой, то векторная сумма может быть заменена алгебраической суммой:
В=В1+В2. (1)
При этом слагаемые В1 и В2 должны быть взяты с соответствующими знаками. В данной задаче во всех трех случаях модули индукций В1 и В2 одинаковы, так как точки выбраны на равных расстояниях от проводов, по которым текут равные токи. Вычислим эти индукции по формуле
B= m0 I /(2pr). (2)
Подставив значения величин в формулу (2), найдем модули В1 и В2:
В1=В2=80 мкТл.
1-й случай. Векторы B1 и В2 направлены по одной прямой (рис. 21.3, а); следовательно, результирующая индукция В определяется по формуле (1). Приняв направление вверх положительным, вниз — отрицательным, запишем: В 1 =— 80 мкТл, В 2=80 мкТл.
Подставив в формулу (1) эти значения В 1 и B 2, получим
В=В 1 +В2=0.
2-й случай. Векторы В 1 и В 2 направлены по одной прямой в одну сторону (рис. 21.3, б). Поэтому можем записать
В 1 =В 2 =— 80 мкТл.
Подставив в формулу (1) значения B 1 и В 2 получим
В=В 1 +В 2 =— 160 мкТл.
3-й случай. Векторы индукций магнитных полей, создаваемых токами в точке, лежащей посередине между проводами, взаимно перпендикулярны (рис. 21.3, в). Результирующая индукция по модулю и направлению является диагональю квадрата, построенного на векторах В 1 и В 2. По теореме Пифагора найдем
 (3)
(3)
Подставив в формулу (3) значения В 1 и В 2 и вычислив, получим Рис. 21.4 B =113 мкТл.
 Пример 3. Определить магнитную индукцию В поля, создаваемого отрезком бесконечно длинного прямого провода, в точке, равноудаленной от концов отрезка и находящейся на расстоянии r 0 =20 см от середины его (рис. 21.4). Сила тока I, текущего по проводу, равна 30 А, длина l отрезка равна 60 см.
Пример 3. Определить магнитную индукцию В поля, создаваемого отрезком бесконечно длинного прямого провода, в точке, равноудаленной от концов отрезка и находящейся на расстоянии r 0 =20 см от середины его (рис. 21.4). Сила тока I, текущего по проводу, равна 30 А, длина l отрезка равна 60 см.
Решение. Для определения магнитной индукции поля, создаваемого отрезком провода, воспользуемся законом Био — Савара—
— Лапласа:
 (1)
(1)
Прежде чем интегрировать выражение (1), преобразуем его так, чтобы можно было интегрировать по углу a. Выразим длину элемента d l проводника через da. Согласно рис. 21.4, запишем

Подставим это выражение d l в формулу (1): Рис. 21.4

Но r — величина переменная, зависящая от a и равная  Подставив r в предыдущую формулу, найдем
Подставив r в предыдущую формулу, найдем
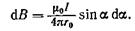 (2)
(2)
Чтобы определить магнитную индукцию поля, создаваемого отрезком проводника, проинтегрируем выражение (2) в пределах от a1 до a2:

Заметим, что при симметричном расположении точки A относительно отрезка провода cos a2= – cos a1. С учетом этого формула (3) примет вид

Из рис. 21.4 следует 
Подставив выражение cos a1 в формулу (4), получим

Подставим числовые значения в формулу (5) и произведем вычисления:

Пример 4. Длинный провод с током I =50 А изогнут под углом a=2p/3. Определить магнитную индукцию В в точке А (рис. 21.5). Расстояние d=5 см.
Решение. Изогнутый провод можно рассматривать как два длинных провода, концы которых соединены в точке О. В соответствии с принципом суперпозиции магнитных полей магнитная индукция В в точке А будет равна геометрической сумме магнитных индукций B1 и В2 полей, создаваемых отрезками длинных проводов
1 и 2, т. е. В = В 1 +В 2. Магнитная индукция В 2равна нулю. Это следует из закона Био — Савара — Лапласа, согласно которому в точках, лежащих на оси проводника, d В =0([dlr]=0).
Магнитную индукцию В 1 найдем, воспользовавшись формулой (3), полученной в примере 3:

где г0 — кратчайшее расстояние от проводника 1 до точки А (рис.21.6)
В нашем случае α1→0 (проводник длинный), α2=α= =2π/3 (cos α2=cos (2π/3))=–½. Расстояние г0 =d sin (π−α)= d sin(π/3)=  . Тогда магнитная индукция
. Тогда магнитная индукция
 Так как В = В 1(В 2=0), то
Так как В = В 1(В 2=0), то
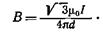
Вектор В сонаправлен с вектором В 1 и определяется правилом правого винта. На рис. 21.6 это направление отмечено значком X (перпендикулярно плоскости чертежа от нас).
. 

Проверка единиц аналогична выполненной в примере 1.
Произведем вычисления:

Пример 5. По тонкому проводящему кольцу радиусом R = 10 см течет ток I =80 А. Найти магнитную индукцию В в точке A, равноудаленной от всех точек кольца на расстояние г=20 см.
Решение. Для решения задачи воспользуемся законом Био — Савара — Лапласа:
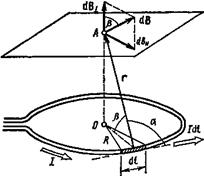
 где dB —магнитная индукция поля, создаваемого элементом тока I dl в точке, определяемой радиусом-вектором г.
где dB —магнитная индукция поля, создаваемого элементом тока I dl в точке, определяемой радиусом-вектором г.
Выделим на кольце элемент d I и от него в точку А проведем радиус-вектор г (рис. 21.7). Вектор d B направим в соответствии с правилом буравчика.
Согласно принципу суперпозиции магнитных полей, магнитная индукции В в точке А определяется интегралом

Рис. 21.7
где интегрирование ведется по всем элементам dI кольца Разложим вектор d B на две составляющие: dB┴ – перпендикулярную плоскости кольца и d B ║ — параллельную плоскости кольца, т. е.
d B= d B^+ d B ½½. Тогда

Заметив, что 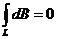 из соображений симметрии и что векторы d B┴ от различных элементов d I сонаправлены, заменим векторное суммирование, заменим векторное суммирование (интегрирование) скалярным:
из соображений симметрии и что векторы d B┴ от различных элементов d I сонаправлены, заменим векторное суммирование, заменим векторное суммирование (интегрирование) скалярным:

где 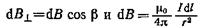 (поскольку d I перпендикулярен r и, следовательно, sina=1). Таким образом,
(поскольку d I перпендикулярен r и, следовательно, sina=1). Таким образом, 
После сокращения на 2π и замены cos β на R/r (рис. 21.7) получим 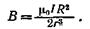 Выразим все величины в единицах СИ, произведем вычисления:
Выразим все величины в единицах СИ, произведем вычисления:
 или
или 
Вектор В направлен на осикольца (пунктирная стрелка на рис.21.7) в соответствии с правилом буравчика.
Пример 6. бесконечно длинный проводник изогнут так, как это изображено на рис. 21.8. Радиус дуги окружности R =10 см. Определить магнитную индукцию В поля, создаваемого в токе О током I =80 A, текущим по этому проводнику.
Решение. Магнитную индукцию В в точке О найдем, используя принцип суперпозиции магнитных полей В=∑Вi. В нашем случае проводник можно разбить на три части (рис. 21.9) два прямолинейных проводника (1 и 3), одним концом уходящие в бесконечность, и дугу полуокружности (2) радиуса R. Тогда
B = B 1+ B 2+ B 3
где B 1, В 2 и В 3 — магнитные индукции поля в точке О, создаваемые током, текущим соответственно на первом, втором и третьем участках проводника.


Так как точка О лежит на оси проводника 1, то В 1=0 и тогда
B=B2+B3
Учитывая, что векторы В 2 и В 3 направлены в соответствии с правилом буравчика перпендикулярно плоскости чертежа от нас, геометрическое суммирование можно заменить алгебраическим:
В=В2+В3.
Магнитную индукцию поля В 2 можно найти, используя выражение для магнитной индукции в центре кругового проводника с током I:

Так как магнитная индукция В 2 создается в точке О половиной такого кругового проводника с током, то, учитывая равный вклад в магнитную индукцию от каждой половинки проводника, можно написать
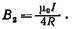
Магнитную индукцию В 3 найдем, используя формулу (3) примера 3:

 В нашем случае
В нашем случае
Тогда

Используя найденные выражения для В2 и В3 получим

или 
Произведем вычисления:

Задачи
Связь между напряженностью и индукцией
магнитного поля в вакууме
21.1. Напряженность Н магнитного поля равна 79,6 кА/м. Определить магнитную индукцию В 0 этого поля в вакууме.
21.2. Магнитная индукция В поля в вакууме равна 10 мТл. Найти напряженность Н магнитного поля.
21.3. Вычислить напряженность Н магнитного поля, если его индукция в вакууме В0=0,05 Тл.
Поле кругового тока и соленоида
21.4. Найти магнитную индукцию в центре тонкого кольца, которому идет ток I =10 А. Радиус r кольца равен 5 см.
 21.5. По обмотке очень короткой катушки радиусом r=16 см течет ток I =5 А. Сколько витков N проволоки намотано на катушку, если напряженность H магнитного поля в ее центре равна 800 А/м?
21.5. По обмотке очень короткой катушки радиусом r=16 см течет ток I =5 А. Сколько витков N проволоки намотано на катушку, если напряженность H магнитного поля в ее центре равна 800 А/м?
21.6. Напряженность Н магнитного поля в центре кругового витка радиусом r=8 см равна 30 А/м. Определить напряженность H 1.
21.7. При какой силе тока I, текущего по тонкому проводящему кольцу радиусом R= 0,2 м, магнитная индукция В в точке, равноудаленной от всех точек кольца на расстояние г=0,3 м, станет равной 20 мкТл?
21.8. По проводнику в виде тонкого кольца радиусом R = 10 см течет ток. Чему равна сила тока I, если магнитная индукция В поля в точке А (рис. 21.10) равна 1 мкТл? Угол β=10°.
21.9. Катушка длиной l =20 см содержит N= 100 витков. По обмотке катушки идет ток 1 =5 А. Диаметр d катушки равен 20 см. Определить магнитную индукцию В в точке, лежащей на оси катушки на расстоянии а =10 см от ее конца.
21.10. Длинный прямой соленоид из проволоки диаметром d =0,5 мм намотан так, что витки плотно прилегают друг к другу.
Какова напряженность Н магнитного поля внутри соленоида при силе тока I =4 А? Толщиной изоляции пренебречь.
21.11. Обмотка катушки диаметром d =10 см состоит из плотно прилегающих друг к другу витков тонкой проволоки. Определить минимальную длину l min катушки, при которой магнитная индукция в середине ее отличается от магнитной индукции бесконечного соленоида, содержащего такое же количество витков на единицу длины, не более чем на 0,5 %. Сила тока, протекающего по обмотке, в обоих случаях одинакова.
 21.12. Обмотка соленоида выполнена тонким проводом с плотно прилегающими друг к другу витками. Длина l катушки равна 1 м, ее диаметр d =2 см. По обмотке идет ток. Вычислить размеры участка на осевой линии, в пределах которого магнитная индукция может быть вычислена по формуле бесконечного соленоида с погрешностью, не превышающей 0,1 %.
21.12. Обмотка соленоида выполнена тонким проводом с плотно прилегающими друг к другу витками. Длина l катушки равна 1 м, ее диаметр d =2 см. По обмотке идет ток. Вычислить размеры участка на осевой линии, в пределах которого магнитная индукция может быть вычислена по формуле бесконечного соленоида с погрешностью, не превышающей 0,1 %.
21.13. Тонкая лента шириной l =40 см свернута в трубку радиусом R =30 см. По ленте течет равномерно распределенный по ее ширине ток I =200 А (рис. 21.11). Определить магнитную индукцию В на оси трубки в двух точках: 1) в средней точке; 2) в точке, совпадающей с концом трубки.
Поле прямого тока
21.14. По прямому бесконечно длинному проводнику течет ток I =50 А. Определить магнитную индукцию В в точке, удаленной на расстояние r=5 см от проводника.
21.15. Два длинных параллельных провода находятся на расстоянии r=5 см один от другого. По проводам текут в противоположных направлениях одинаковые токи I =10 А каждый. Найти напряженность H магнитного поля в точке, находящейся на расстоянии r1=2 см от одного и г2=3 см от другого провода.
21.16. Расстояние d между двумя длинными параллельными проводами равно 5 см. По проводам в одном направлении текут одинаковые токи I =30 А каждый. Найти напряженность Н магнитного поля в точке, находящейся на расстоянии г1=4 см от одного и г2=3 см от другого провода.
21.17. По двум бесконечно длинным прямым параллельным проводам текут токи I =50 А и I 2=100 А в противоположных направлениях. Расстояние d между проводами равно 20 см. Определить магнитную индукцию В в точке, удаленной на г1=25 см от первого и на r2=40 см от второго провода.
21.18. По двум бесконечно длинным прямым параллельным проводам текут токи I 1=20 А и I 2=30 А в одном направлении. Расстояние d между проводами равно 10 см. Вычислить магнитную индукцию В в точке, удаленной от обоих проводов на одинаковое расстояние г=10 см.
21.19. Два бесконечно длинных прямых провода скрещены под прямым углом (рис. 21.12). По проводам текут токи I 1=80 А и I 2=60 А. Расстояние d между проводами равно 10 см. Определит магнитную индукцию В в точке А, одинаково удаленной от обоих проводников.

21.20. По двум бесконечно длинным прямым проводам, скрещенным под прямым углом, текут токи I 1=30 А и I 2=40 А. Расстояние d между проводами равно 20 см. Определить магнитную индукцию В в точке С (рис. 21.12), одинаково удаленной от обоих проводов на расстояние, равное d.
 21.21. Бесконечно длинный прямой провод согнут под прямым углом. По проводнику течет ток I =20 А. Какова магнитная индукция В в точке А (рис. 21.13), если г=5 см?
21.21. Бесконечно длинный прямой провод согнут под прямым углом. По проводнику течет ток I =20 А. Какова магнитная индукция В в точке А (рис. 21.13), если г=5 см?
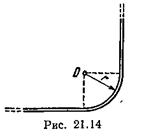
21.22. По бесконечно длинному прямому проводу, изогнутому так, как это показано на рис. 21.14, течет ток I =100 А Определить магнитную индукцию В в точке О, если г=10см.
21.23. Бесконечно длинный прямой провод согнут под прямым углом. По проводу течет ток I =100 А. Вычислить магнитную индукцию В в точках, лежащих на биссектрисе угла и удаленных от вершины угла на а =10 см.
21.24. По бесконечно длинному прямому проводу, согнутому под углом α=120°, течет ток I =50 А. Найти магнитную индукцию В в точках, лежащих на биссектрисе угла и удаленных от вершины его на расстояние а=5 см.
21.25. По контуру в виде равностороннего треугольника идет ток I =40 А. Длина а стороны треугольника равна 30 см. Определить магнитную индукцию В в точке пересечения высот.
21.26. По контуру в виде квадрата идет ток I =50 А. Длина а стороны квадрата равна 20 см. Определить магнитную индукцию В в точке пересечения диагоналей.
21.27. По тонкому проводу, изогнутому в виде прямоугольника, течет ток I =60 А. Длины сторон прямоугольника равны а =30 см и b =40 см. Определить магнитную индукцию В в точке пересечения диагоналей.
21.28. Тонкий провод изогнут в виде правильного шестиугольника. Длина d стороны шестиугольника равна 10 см. Определить магнитную индукцию В в центре шестиугольника, если по проводу течет ток I =25А 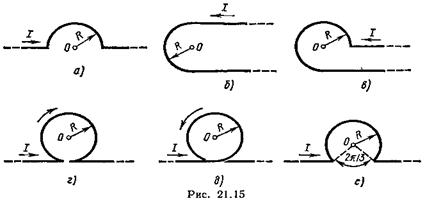
21.29. По проводу, согнутому в виде правильного шестиугольника с длиной а стороны, равной 20 см, течет ток I =100 А. Найти напряженность H магнитного поля в центре шестиугольника. Для сравнения определить напряженность H 0 поля в центре кругового провода, совпадающего с окружностью, описанной около данного шестиугольника.
21.30. По тонкому проволочному кольцу течет ток. Не изменяя силы тока в проводнике, ему придали форму квадрата. Во сколько раз изменилась магнитная индукция в центре контура?
21.31. Бесконечно длинный тонкий проводник с током I =50 А имеет изгиб (плоскую петлю) радиусом R = 10 см. Определить в точке О магнитную индукцию В поля, создаваемого этим током, в случаях а—е, изображенных на рис. 21.15.
21.32. По плоскому контуру из тонкого провода течет ток I =100 А. Определить магнитную индукцию В поля, создаваемого этим током в точке О, в случаях а—е, изображенных на рис. 21.16. Радиус R изогнутой части контура равен 20 см.

Не нашли, что искали? Воспользуйтесь поиском: