Примеры решения задач. · Циркуляция вектора магнитной индукции В вдоль замкну­того контура

ЗАКОН ПОЛНОГО ТОКА. МАГНИТНЫЙ ПОТОК. МАГНИТНЫЕ ЦЕПИ

Основные формулы

· Циркуляция вектора магнитной индукции В вдоль замкну­того контура

где B_i — проекция вектора магнитной индукции на направление элементарного перемещения dl вдоль контура L. Циркуляция век­тора напряженности Н вдоль замкнутого контура

,

· Закон полного тока (для магнитного поля в вакууме)

где m₀ — магнитная постоянная; — алгебраическая сумма токов, охватываемых контуром; п — число токов.

Закон полного тока (для произвольной среды)

· Магнитный поток Ф через плоский контур площадью S:

а) в случае однородного поля

Ф= BS cos a; или Ф = B _n S,

где a — угол между вектором нормали n к плоскости контура и век­тором магнитной индукции В; В _n — проекция вектора В на нормаль n (B _n =B cos a);

б) в случае неоднородного поля

где интегрирование ведется во всей поверхности S.

· Потокосцепление, т.е. полный магнитный поток, сцепленный со всеми витками соленоида или тороида,

где Ф — магнитный поток через один виток; N — число витков со­леноида или тороида.

· Магнитное поле тороида, сердечник которого составлен из двух частей, изготовлен­ных из веществ с раз­личными магнитными проницаемостями:

а) магнитная индук­ция на осевой линии тороида

где I — сила тока в об­мотке тороида; N — чис­ло ее витков; l ₁ и l₂ -­ длины первой и второй частей сердечника торо­ида; m₁ и m₂ —магнитные проницаемости ве­ществ первой и второй частей сердечника торо­ида; m₀ —магнитная постоянная

б) напряженность магнитного поля на осе­вой линии тороида в первой и второй частях сердечника

H ₁= B /(m₁ m₂); H ₁= B /(m₂ m₀ );

в) магнитный поток в сердечнике тороида

или по аналогии с законом Ома (формула Гопкинсона)

Ф_m= F _m/ R _m,

где F _m — магнитодвижущая сила; R _m — полное магнитное сопро­тивление цепи;

г) магнитное сопротивление участка цепи

R_m=l/ (μμ₀S).

• Магнитная проницаемостьμ, ферромагнетика связана с маг­нитной индукцией В поля в нем и напряженностью Н намагничи­вающего поля соотношением

μ= B/ (μ₀ H).

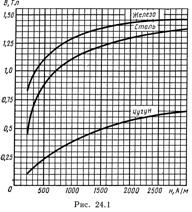
• Связь между магнитной индукцией В поля в ферромагнетике и напряженностью Н намагничивающего поля выражается графи­чески (рис. 24.1).

Примеры решения задач

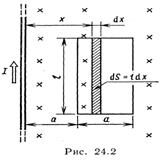
Пример 1. В одной плоскости с бесконечно длинным прямым проводом, по которому течет ток I =50 А, расположена прямоуголь­ная рамка так, что две большие стороны ее длиной l =65 см парал­лельны проводу, а расстояние от провода до ближайшей из этих сторон равно ее ширине. Каков магнитный поток Ф, пронизываю­щий рамку?

Решение. Магнитный поток Ф через поверхность площадью S определяется выражением

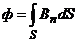
В нашем случае вектор магнитной индукции В перпендикулярен плоскости рамки. Поэтому для всех точек рамки В_n=В. Магнитная индукция В, создаваемая бесконечно длинным прямым проводником с током, определяется формулой

,

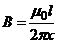где x— расстояние от провода до точки, в которой определяется В.

Для вычисления магнитного потока заметим, что так как В зависит от х и элементарный поток Ф будет также за­висеть от х, то

dф=B(x)dS.

Разобьем площадь рамки на узкие элементарные площадки длиной l, шири­ной dx и площадью dS=ldx (рис. 24.2). В пределах этой площадки магнитную индукцию можно считать постоянной, так как все части площад­ки равноудалены (на расстояние х) от провода. С учетом сделанных замечаний элементарный магнитный поток можно записать в виде

dФ=

Проинтегрировав полученное выражение в пределах от x ₁ =a до х₂=2а, найдем

|_p^2p.

Подставив пределы, получим

Убедимся в том, что правая часть полученного равенства дает единицу магнитного потока (Вб): [m₀] [ I ] [ l ]= Гн/м ×1 А ×1 м=1 Вб. Произведя вычисления по формуле (1), найдем Ф=4,5 мкВб.

Пример 2. Определить индукцию В и напряженность Н магнит­ного поля на оси тороида без сердечника, по обмотке которого, со­держащей N =200 витков, идет ток I =5 А. Внешний диаметр d ₁ тороида равен 30 см, внутренний d ₂ = 20 см.

Решение. Для определения напряженности магнитного поля внутри тороида вычислим циркуляцию вектора Н вдоль линии маг­нитной индукции поля:

Из условия симметрии следует, что линии магнитной индукции тороида представляют собой окружности и что во всех точках этой линии напряженности одинаковы. Поэтому в выражении циркуля­ции напряженность Н можно вынести за знак интеграла, а интегри­рование проводить в пределах от нуля до 2 p r, где r — радиус ок­ружности, совпадающей с линией индукции, вдоль которой вычис­ляется циркуляция, т. e.

(1)

С другой стороны, в соответствии с законом полного тока цир­куляция вектора напряженности магнитного поля равна сумме то­ков, охватываемых контуром, вдоль которого вычисляется цирку­ляция:

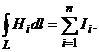(2)

Приравняв правые части равенств (1) и (2), получим

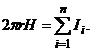(2)

Линия, проходящая вдоль тороида, охватывает число токов, равное числу витков тороида. Сила тока во всех витках одинакова. Поэтому формула (3) примет вид 2prH=-NI, откуда

(4)

Для средней линии тороида r=1/2(R₁R₂)=1/4(d₁+d₂). Подставив это выражение r в формулу (4), найдем

(5)

Магнитная индукция В ₀ в вакууме связана с напряженностью поля соотношением B ₀ = m₀ H. Следовательно,

(6)

Подставив значения величин в выражения (5) и (6), получим:

H =1,37 кА/м, B ₀=1,6 мТл.

Пример. 3. Чугунное кольцо имеет воздушный зазор длиной l о=5 мм. Длина l средней линии кольца равна 1 м. Сколько витков N содержит обмотка на кольце, если при силе тока I =4 А индукция В магнитного поля в воздушном зазоре равна 0,5 Тл? Рассеянием маг­нитного потока в воздушном зазоре можно пренебречь. Явление гистерезиса не учитывать.

Решение. Пренебрегая рассеянием магнитного потока, мы можем принять, что индукция поля в воздушном зазоре равна ин­дукции поля в чугуне. На основании закона полного тока запишем

IN=Hl+H ₀ I ₀.

По графику (см. рис. 24.1) находим, что при В=0,5 Тл напря­женность Н магнитного поля в чугуне равна 1,2 кА/м. Так как для воздуха m=1, то напряженность поля в воздушном зазоре

H ₀= Bm ₀=0,4 MA/м.

Искомое число витков

N=(Hl+H ₀ l _o )/I==800.

Задачи

Закон полного тока

24.2. Вычислить циркуляцию вектора индукции вдоль конту­ра, охватывающего токи I ₁= 10 А, I ₂= 15 А, текущие в одном направ­лении, и ток I₃ =20 А, текущий в противоположном направлении.

24.3. По сечению проводника равномерно распределен ток плот­ностью j =2 МА/м². Найти циркуляцию вектора напряженности вдоль окружности радиусом R =5 мм, проходящей внутри провод­ника и ориентированной так, что ее плоскость составляет угол a=30° с вектором плотности тока.

24.4. Диаметр D тороида без сердечника по средней линии равен 30 см. В сечении тороид имеет круг радиусом r=5 см. По обмотке тороида, содержащей N=2000 витков, течет ток I= 5 А (рис. 24.4). Пользуясь законом полного тока, определить максимальное и мини­мальное значение магнитной индукции В в тороиде.

Магнитный поток

24.5. Найти магнитный поток Ф, создаваемый соленоидом сече­нием S= 10 см², если он имеет п = 10 витков на каждый санти­метр его длины при силе тока I =20 А.

24.6. Плоский контур, площадь S которого равна 25 см², нахо­дится в однородном магнитном поле с индукцией B =0,04 Тл. Оп­ределить магнитный поток Ф, пронизывающий контур, если плос­кость его составляет угол b=30° с линиями индукции.

24.7. При двукратном обводе магнитного полюса вокруг провод­ника с током I =100 А была совершена работа A =1 мДж. Найти магнитный поток Ф, создаваемый полюсом.

24.8. Соленоид длиной l =1 м и сечением S = 16 см² содержит N =2000 витков. Вычислить потокосцепление Y при силе тока I в обмотке 10 А.

24.9. Плоская квадратная рамка со стороной а=20 см лежит в одной плос­кости с бесконечно длинным прямым проводом, по которому течет ток I =100 А. Рамка расположена так, что ближайшая к проводу сторона параллельна ему и находится на расстоя­нии I =10 см от провода. Определить магнитный поток Ф, пронизывающий рамку.

24.10. Определить, во сколько раз отличаются магнитные потоки, прони­зывающие рамку при двух ее положениях относительно прямого проводника с током, представленных на рис. 24.5.

24.11. Квадратная рамка со стороной длиной а=20 см расположе­на в одной плоскости с прямым бесконечно длинным проводом с то­ком. Расстояние l от провода до середины рамки равно 1 м. Вычис­лить относительную погрешность, которая будет допущена при рас­чете магнитного потока, пронизывающего рамку, если поле в пределах рамки считать однородным, а магнитную индукцию — равной значению ее в центре рамки.

24.12. Тороид квадратного сечения содержит N=l000 витков. Наружный диаметр D тороида равен 40 см, внутренний d =20 см. Найти магнитный поток Ф в тороиде, если сила тока I, протекаю­щего по обмотке, равна 10 А.

Указание. Учесть, что магнитное поле тороида неоднородно.

Не нашли, что искали? Воспользуйтесь поиском: