
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Вычисление основных термодинамических характеристик Церия (Се) при температуре виртуального фазового перехода.
Входные данные (3 вариант):
| Фазовый переход (Ce) | Тα→β,K | ∆H, Дж/моль | ∆S, Дж/(моль∙К) | ∆Cp, Дж/(моль∙К) |
| FCC→BCC | 1000,00 | 2991,66 | 2,9916 | -0,1165 |
| BCC→L | 1072,00 |  5460,12 5460,12
| 5,0934 | 0,0836 |
Теория:
Температуру виртуального фазового
перехода будем находить методом
дихотомии– последовательного
деления пополам.
Введем новую переменную
 , t<<1 (1)
, t<<1 (1)
 (2)
(2)
| ∆Ga→δ(T)= ∆Ga→b(T)+∆Gb→δ(T) |
Теперь, с помощью “t” и “DS”, опишем энергию Гиббса:

 (3)
(3)  (4)
(4)
 :
:

 (5)
(5)
(5) → (4): 
ÞПолучаем «рабочую формулу»:
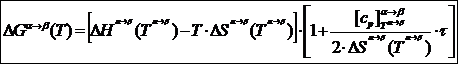
|
Алгоритм расчета:
Обозначения в программе:
Температура перехода FCC, (Tγ→δ): Tgd
Температура перехода BCC, (Tδ→l): Tdl
Энтальпия перехода FCC (∆Hγ→δ): DHgd
Энтальпия перехода BCC (∆Hδ→l): DHdl
Энергия Гиббса перехода FCC (∆Gγ→δ): DGgd
Энергия Гиббса перехода BCC ∆Gδ→l): DGdl
Энтропия перехода FCC (∆Sγ→δ): DSgd
Энтропия перехода BCC (∆Sδ→l): DSdl
Разность разносторонних пределов
теплоемкости перехода FCC [Cpγ→δ]: DCp_gd
то же дляперехода BCC [Cpδ→l]: DCp_dl
Погрешность (εt): Еt
Значение ∆G при т-ре виртуального фазового перехода: DGgl_1
n – количество циклов программы
Т1, Т2, Tb, Tl, dT – вспомогательные переменные

Блок-схема программы:
Текст программы:
Program faz_perehod;
label M1, M2;
Var n, Tb, Tl, Et, T1, T2, Tgd, Tdl, dT, DGgd, DGdl, DHgd, DHdl, DSgd, DSdl, DCp_gd, DCp_dl, DGgl_1:real;
begin
{writeln('Tb=');readln(Tb); Результат вычислений программы:
 writeln('Tl=');readln(Tl);
writeln('Tl=');readln(Tl);
writeln('Et=');readln(Et);}
writeln('-----------------');
n:=0;
dT:=0;
Tb:=1000; Tgd:=1000;
Tl:=1072; Tdl:=1072;
{Et:=0.001;}
T2:=0.5*(Tgd+Tdl);
DHgd:=2991.66;
DHdl:=5460.12;
DSgd:=2.9916;
DSdl:=5.0934;
DCp_gd:=-0.1165;
DCp_dl:=0.0836;
writeln ('vvedite pogresnost Et');
readln (Et);
M2:
n:=n+1;
T1:=0.5*(Tb+Tl);
writeln;
DGgd:=(DHgd-T1*DSgd)*(1+DCp_gd/(2*DSgd)*(T1/Tgd-1));
DGdl:=(DHdl-T1*DSdl)*(1+DCp_dl/(2*DSdl)*(T1/Tdl-1));
DGgl_1:=DGgd+DGdl;
write (' n=',n:5:0); write (' T2=',T2:5:3);
if DGgl_1>0 then begin
Tb:=T1;
T2:=0.5*(Tb+Tl);
end;
if DGgl_1<0 then
begin
Tl:=T1;
T2:=0.5*(Tb+T1)
end;
dT:=abs(T2-T1);
write (' dT=',dT:5:3); write (' DGgl_1= ',DGgl_1:5:3);
{write (' DGgd=',DGgd:5:3); write (' DGdl=',DGdl:5:3);}
if dT<Et then goto M1;
if dT>Et then goto M2;
M1:
writeln;
writeln;
writeln (' T perehoda alfa-gamma: T2=', T2:5:5);
writeln (' n=',n:2:0);
writeln ('----------');
end.
Расчет в Excel:


Подробно окрестность, где Энергия Гиббса перехода BCC ∆Gδ→l(DGgl_1) обращается в ноль:



 Теперь, зная температуру виртуального фазового перехода, мы можем вычислить остальные термодинамические параметры: ∆Sγ→l, ∆Hγ→l и [Cpγ→l]:
Теперь, зная температуру виртуального фазового перехода, мы можем вычислить остальные термодинамические параметры: ∆Sγ→l, ∆Hγ→l и [Cpγ→l]:
1) ∆Sγ→l(Tγ→l)= 
Найдем частные производные  и
и  ; Используем «рабочую формулу»:
; Используем «рабочую формулу»:

Для нахождения частной производной  , обозначим выражение через константы:
, обозначим выражение через константы:

 =[a-T×b]×[c+d×T], где
=[a-T×b]×[c+d×T], где
Получаем:

Вычисляем в Excel: (для  получаем автоматически):
получаем автоматически):

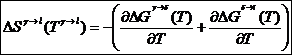

2) 
 Умножаем полученную энтропию на температуру виртуального фазового перехода – получаем энтальпию.
Умножаем полученную энтропию на температуру виртуального фазового перехода – получаем энтальпию.
 1045,377*8,078= 8444,181
1045,377*8,078= 8444,181

3)
с помощью тех же элементарных замен получаем:

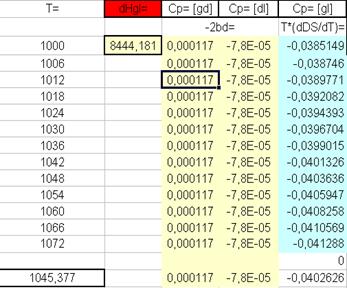 (аналогично для
(аналогично для  )
)

Вычисляем в Excel, получаем
 = 1045,377*(0,000117 - 7,79851E-05)
= 1045,377*(0,000117 - 7,79851E-05)
= -0,04026262
Проверим полученные значения. Знаем:

Вычисляем левую и правую часть равенства.
 Сравниваем значения.
Сравниваем значения.
Равенство выполнено.
Найдем погрешности наших вычислений.





Найдем относительную погрешность D[Cp]g→l:
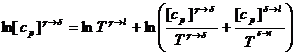 ;
;
Дифференцируем:


Таблица выходных данных:
| Тg→l ,K | DHg→l Дж/моль | DSg→l Дж/(моль∙К) | D[Cp]g→l Дж/(моль∙К) | DGg→l Дж/моль |
| 1045.38±0.01 | 8.44±0.01 | 8.0776±0.0001 | 0.04±0.0004 |
| <== предыдущая лекция | | | следующая лекция ==> |
| О будущих больших звездах большого балета | | | Отчет по лабораторной работе |
Не нашли, что искали? Воспользуйтесь поиском:
 ,
,
