
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Экспериментальная установка. Методика эксперимента
Определение теплоты испарения жидкости
Краткая теория
Испарением называют переход вещества из жидкого в газообразное состояние. При испарении с поверхности жидкости вылетают молекулы, образуя над ней пар. Вылететь из жидкости в окружающее пространство могут только наиболее быстрые молекулы, поскольку только они в состоянии преодолеть силы притяжения, действующие в поверхностном слое жидкости. В результате ухода быстрых молекул жидкость охлаждается. Для поддержания ее температуры постоянной требуется подвод теплоты.
Количество теплоты, которое необходимо сообщить веществу, для того чтобы превратить его из жидкого состояния в газообразное при постоянной температуре и постоянном давлении, называется теплотой испарения (или теплотой парообразования).
Теплоту парообразования жидкостей можно измерить непосредственно при помощи калориметра. Такой метод, однако, не позволяет получить точных результатов из-за неконтролируемых потерь тепла, которое трудно сделать малыми. В настоящей работе для определения теплоты испарения применим косвенный метод, основанный на уравнении Клапейрона-Клаузиуса:
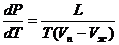 . (1)
. (1)
Здесь P – давление насыщенного пара жидкости при температуре T, T - абсолютная температура жидкости и пара, 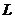 - удельная теплота испарения жидкости,
- удельная теплота испарения жидкости, 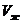 - удельный объем жидкости,
- удельный объем жидкости,  - удельный объем пара.
- удельный объем пара.
Если известна зависимость удельной теплоты испарения 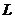 и удельных объемов
и удельных объемов 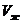 и
и  от температуры, то уравнение (1) можно проинтегрировать и найти в явном виде зависимость давления насыщенного пара от температуры. В самом грубом приближении можно считать, что величина
от температуры, то уравнение (1) можно проинтегрировать и найти в явном виде зависимость давления насыщенного пара от температуры. В самом грубом приближении можно считать, что величина 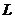 не зависит от температуры, а удельным объемом жидкости по сравнению с удельным объемом пара можно пренебречь. Кроме того, можно считать, что к пару применимо уравнение состояния идеального газа (уравнение Менделеева-Клапейрона), из которого выразим удельный объём пара:
не зависит от температуры, а удельным объемом жидкости по сравнению с удельным объемом пара можно пренебречь. Кроме того, можно считать, что к пару применимо уравнение состояния идеального газа (уравнение Менделеева-Клапейрона), из которого выразим удельный объём пара: 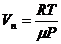 .
.
В принятом приближении уравнение (1) перейдет в дифференциальное уравнение:
 ,
,
интегрируя которое, получим:
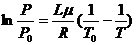 , (2)
, (2)
где  - давление насыщенного пара при начальной температуре
- давление насыщенного пара при начальной температуре 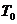 .
.
Соотношение (2) позволяет определить удельную теплоту испарения, зная зависимость давления насыщенного пара от температуры. Определению удельной теплоты испарения воды и посвящается настоящая лабораторная работа.
Экспериментальная установка. Методика эксперимента
Эксперимент проводится на установке, схематично показанной на рисунке. Установка состоит из термостата, заполненного водой, нагревательных элементов, системы охлаждения (на рисунке не показана), двух колб с исследуемыми газами и измерительных приборов.
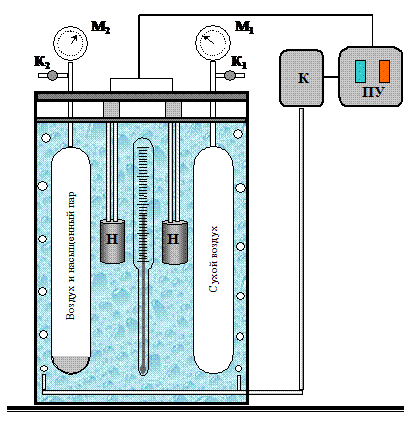 |
Нагревательные элементы Н служат для увеличения температуры в системе. Для равномерного нагрева системы вода постоянно перемешивается воздухом, подаваемым компрессором К. Включение и выключение нагревательных элементов и компрессора осуществляется с помощью пульта управления ПУ. Перед началом работы краны К1 и К2 открываются, затем закрываются. Это необходимо для того, чтобы давление в колбах в начальный момент сравнялось с атмосферным давлением. Термометр измеряет температуру Т воды, в которую погружены колбы с сухим и влажным воздухом. Параметры установки таковы, что нагревание воды происходит медленно и газ в колбах успевает прогреваться до той же температуры, что и вода в системе. Манометры М1 и М2 показывают избыточное давление в колбах с сухим и влажным воздухом соответственно.
По результатам измерений можно рассчитать давление насыщенного пара по формуле:
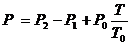 , (3)
, (3)
где P1 и P2 - показания манометров М1 и М2 соответственно, Т – температура в системе
 - давление насыщенного пара при начальной температуре
- давление насыщенного пара при начальной температуре 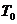 (данная величина считается известной).
(данная величина считается известной).
По данным опыта строится график зависимости 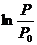 от
от 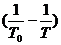 .
.
Согласно уравнению (2) экспериментальные точки должны ложиться на прямую, проходящую через начало координат. По графику определяется угловой коэффициент этой прямой 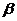 и находится удельная теплота испарения воды.
и находится удельная теплота испарения воды.
Из уравнения (2) видно, что 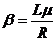 и, следовательно:
и, следовательно: 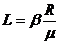 .
.
Не нашли, что искали? Воспользуйтесь поиском: