
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
УКАЗАНИЯ К ОФОРМЛЕНИЮ РАБОТЫ
МЕХАНИКА ГРУНТОВ
Задания и методические указания
к контрольной работе для студентов
заочной формы обучения специальностей:
270102 – Промышленное и гражданское строительство

Краснодар 2012
УДК 624.131
Механика грунтов. Задания и методические указания к контрольной работе для студентов заочной формы обучения специальностей: 270102 – Промышленное и гражданское строительство/Сост. К.Ш. Шадунц, П.А. Ляшенко, В.Х. Ким, В.В. Пелевин. Кубанский государственный аграрный ун-т, Краснодар, 2012. – 28 с.
Приведены задания для усвоения всех основных разделов механики грунтов, расчетные схемы, указания по выполнению заданий, рекомендуемая литература. Указания снабжены необходимыми справочными данными.
Предназначены для студентов строительных специальностей вузов.
Ил. 9, табл. 19, библ. 13 назв.
Печатается по решению Методической комиссии Инженерно-строительного факультета Кубанского государственного аграрного университета: Протокол № 5 от 30.01.2012 г.
Рецензент: заведующий кафедрой
архитектуры КГАУ, к.т.н.,
профессор В. Д. Таратута
ОГЛАВЛЕНИЕ
| Общие указания…………………………………………………………….. | |
| Содержание работы и порядок ее выполнения..…………………………. | |
| Указания к оформлению работы ………………………………………….. | |
| Задания………………………………………………………………………. | |
| Методические указания к выполнению работы………………………….. | |
| Приложение 1. Таблицы значений некоторых величин к выполнению работы …….…….....................………….. | |
| Литература ………………………………………………………………….. |
ОБЩИЕ УКАЗАНИЯ
Составной частью капитального строительства является фундаментостроение. Механика грунтов - теоретическая база фундаментостроения. Применение ее достижений в проектной и производственной практике позволяет полнее использовать несущую способность грунтов оснований, выбирать наиболее экономичные и рациональные способы возведения фундаментов зданий и инженерных сооружений с учетом инженерно-геологической обстановки.
Учебный план-график предусматривает выполнение студентами-заочниками специальности 2903 индивидуальной контрольной работы по механике грунтов. Контрольная работа является одним из ответственных звеньев учебного процесса и имеет целью закрепить теоретические знания, полученные студентами за период самостоятельного изучения курса. В процессе выполнения контрольной работы студенты должны научиться справочными и литературными материалами.
В связи с предъявляемыми в настоящее время требованиями к унификации применяемых в расчетах физических величин задания и методические указания составлены в соответствии с основными положениями Перечня единиц физических величин, подлежащих применению в строительстве [9].
Самостоятельность решения задач в контрольной работе имеет первостепенное значение для усвоения учебного материала.
СОДЕРЖАНИЕ РАБОТЫ И ПОРЯДОК ЕЕ ВЫПОЛНЕНИЯ
Контрольная работа составлена в соответствия с программой дисциплины и содержит восемь задач по следующим основным разделам: природа грунтов и показатели физико-механических свойств - задача № I; напряжения в грунтах от действия внешних сил - задачи № 2, 3, 4; теория предельного напряженного состояния грунтов, ее приложение - задачи № 5, 6; деформации грунтов и прогноз осадок фундаментов - задачи № 7, 8.
Для выполнения контрольной работы необходимо выбрать данные из таблиц, помещенных в настоящих методических указаниях. Задание выбирается по следующему правилу: задачи выполняются студентом по варианту, соответствующему последней цифре учебного шифра, Например, студент, имевший учебный шифр (номер зачетной книжки) 82-436, выполняет задачи по варианту №6.
Студент обязан выполнить контрольную работу в срок, предусмотренный индивидуальным планом-графиком на учебный год. Выполненную контрольную работу с настоящими указаниями следует направить на кафедру для рецензирования.
Контрольная работа, выполненная по варианту, не соответствующему учебному шифру, и без соблюдения указанных ниже требований к оформлению, на рецензирование не принимается.
Задания и методические указания к контрольной работе выдаются каждому студенту на факультете. Консультации, связанные с выполнением контрольной работы, студент может получить у преподавателя кафедры оснований и фундаментов, ведущего дисциплину "Механика грунтов". Для облегчения выполнения контрольной работы в методических указаниях к каждой задаче приведены краткие рекомендации о последовательности выполнения расчетов, а также об использовании литературных источников.
УКАЗАНИЯ К ОФОРМЛЕНИЮ РАБОТЫ
Контрольная работа должна содержать расчетно-пояснительную записку, в состав которой следует включить: исходные данные, теоретическую часть, отражающую методику расчетов, сами расчеты и их результаты, расчетные схемы со всеми необходимыми обозначениями и размерами, список литературы. Результаты расчетов могут быть представлены в табличной форме. Расчетно-пояснительная записка выполняется на стандартных листах формата А4. Текст следует писать от руки на одной стороне листа чернилами аккуратно, разборчиво. Все расчетные данные и показатели должны сопровождаться единицами измерения. Расчеты необходимо сопровождать ссылками на соответствующую литературу. Список использованной литературы, включая методические указания, по которым выполнялась контрольная работа, помещают в конце записки.
Расчетные схемы выполняются в карандаше на листах чертежной бумаги или миллиметровке того же формата, что и листы расчетно-пояснительной записки. Необходимо помнить, что данные расчета и схемы должны быть строго увязаны между собой, так как они составляют одно целое.
Листы записки должны иметь сквозную нумерации и быть сброшюрованы. На обложке расчетно-пояснительной записки следует указать: университет, кафедру, наименование контрольной работы, факультет, курс, фамилию, имя и отчество студента (полностью), учебный шифр, адрес, дату выполнения контрольной работы, а также год издания методических указаний, по которым выполнялась контрольная работа. Расчетно-пояснительная записка должна быть подписана студентом.
Если в контрольной работе допущены ошибки, и она возвращена студенту без зачета, необходимо сделать все нужные исправления по замечаниям преподавателя на свободных листах с припиской "исправление ошибок". Перечеркивание и исправление написанного текста, расчетов и расчетных схем недопустимо.
ЗАДАНИЯ
Задача № I. По результатам лабораторных исследований свойств грунтов требуется:
а) для образцов песчаного грунта построить интегральную кривую гранулометрического состава, определить тип грунта по гранулометрическому составу и степени его неоднородности, дать оценку плотности сложения и степени влажности, определить расчетное сопротивление R0; для образцов глинистого грунта определить тип грунта, разновидность по консистенции и расчетное сопротивление R0; исходные данные приведены в Таблице 1.
Таблица 1 – Исходные данные к Задаче № 1 (физические характеристики грунтов)
| Номер варианта | Плотность, г/см3 | Влажность, % | Содержание частиц, %, при их размере, мм | ||||||||||
| частиц грунта ρs | грунта ρ | природная W | на границе | более 2,0 | 2,0-0,5 | 0,5-0,25 | 0,25-0,1 | 0,1-0,05 | 0,05-0,01 | 0,01-0,005 | менее 0,005 | ||
| раска тыва ния Wρ | теку чес ти WL | ||||||||||||
| 2,71(2,66) 2,73(2,65) 2,71(2,66) 2,71(2,68) 2,74(2,67) 2,71(2,67) 2,70(2,65) 2,71(2,68) 2,70(2,65) 2,74(2,65) | 1,85(2,02) 1,89(1,72) 1,93(1,75) 1,87(1,89) 1,89(1,79) 1,91(1,92) 1,89(1,82) 1,94(1,72) 1,95(1,86) 1,94(1,89) | 21,4(19,6) 20,1(6,8) 19,2(12,1) 22,3(8,4) 20,5(16,2) 19,8(12,9) 17,3(11,8) 18,9(9,8) 18,2(14,1) 19,1(15,2) | 30,2 20,8 24,3 19,4 26,6 19,6 25,8 23,8 26,5 23,4 | 43,4 31,6 37,4 30,8 47,2 28,9 39,3 43,6 36,6 41,8 | 2,5 1,0 1,2 1,2 0,4 4,5 2,1 3,8 | 19,5 2,0 15,1 31,0 21,5 17,0 13,4 47,5 24,5 29,8 | 25,0 16,0 40,2 25,0 22,7 20,0 32,2 16,8 29,4 29,4 | 20,0 45,0 33,9 10,0 19,3 45,0 31,4 10,2 15,4 18,5 | 20,0 12,0 5,7 27,4 12,6 13,3 8,6 8,0 9,6 11,5 | 10,0 2,0 1,5 3,6 16,1 2,0 9,8 8,0 10,2 4,6 | 2,0 4,0 0,7 1,2 3,6 0,9 2,6 3,5 7,8 1,1 | 1,0 1,0 2,9 0,8 3,0 0,6 1,6 1,5 1,0 1,3 |
Примечания: 1. Данные по гранулометрическому составу относятся к песчаным грунтам
2. Величины основных физических характеристик песчаных
грунтов rs, r, W приведены в скобках.
б) построить график компрессионной зависимости вида L=¦(p), определить для заданного расчетного интервала давлений коэффициент относительной сжимаемости грунта, модуль деформации и охарактеризовать степень сжимаемости грунта; исходные данные приведены в Таблице 2.
в) построить график сдвига вида tпред = ¦(p), определить методом наименьших квадратов нормативное значение угла внутреннего трения jн грунта и нормативное значение удельного сцепления сн грунта; исходные данные приведены в Таблице 3.
Таблица 2 – Исходные данные к Задаче № 1 (компрессионные испытания)
| Номер варианта | Начальный коэффициент пористости грунта е0 | Полная осадка образца грунта Si, мм при нагрузке Pi, МПа | Расчетный интервал давлений, МПа | |||||
| 0,05 | 0,1 | 0,2 | 0,3 | 0,5 | Р1 | Р2 | ||
| 0,574 0,646 0,673 0,540 0,734 0,571 0,677 0,707 0,656 0,681 | 0,13 0,15 0,20 0,14 0,10 0,13 0,25 0,14 0,22 0,14 | 0,33 0,24 0,35 0,29 0,18 0,27 0,50 0,29 0,43 0,29 | 0,62 0,41 0,66 0,46 0,31 0,49 0,87 0,46 0,69 0,43 | 0,78 0,55 0,86 0,59 0,42 0,69 1,10 0,60 0,91 0,56 | 1,02 0,79 1,12 0,75 0,57 0,99 1,39 0,74 1,17 0,70 | 0,05 0,05 0,05 0,05 0,05 0,1 0,05 0,1 0,05 0,05 | 0,2 0,2 0,3 0,3 0,2 0,3 0,3 0,3 0,3 0,2 |
Примечания: 1. Начальная высота образца грунта h = 25 мм.
2. I кгс/см2 = 98066,5 Па»105 Па» 0,1 МПа.
Таблица 3 - Исходные данные к Задаче № 1 (сдвиговые испытания)
| Номер варианта | Предельное сопротивление образца грунта сдвигу τi пред., МПа, при нормальном удельном давлении, передаваемом на образец грунта Pi, МПа | |||||
| 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | |
| 0,070 0,064 0,060 0,074 0,080 0,072 0,040 0,074 0,050 0,104 | 0,135 0,125 0,095 0,150 0,120 0,140 0,075 0,145 0,085 0,145 | 0,199 0,184 0,139 0,225 0,139 0,212 0,101 0,221 0,131 0,180 | 0,265 0,250 0,175 0,300 0,175 0,280 0,130 0,290 0,175 0,220 | 0,330 0,315 0,206 0,375 0,219 0,356 0,156 0,344 0,219 0,256 | 0,398 0,375 0,255 0,450 0,233 0,428 0,188 0,438 0,263 0,293 |
Задача № 2. К горизонтальной поверхности массива грунта в одном створе приложены три вертикальные сосредоточенные силы P1, P2, P3, расстояние между осями действия сил r1 и r2. Определить величины вертикальных составляющих напряжений sz от совместного действия сосредоточенных сил в точках массива грунта, расположенных в плоскости действия сил: I) по вертикали I-I, проходящей через точку приложения силы P2; 2) по горизонтали II-II; проходящей на расстоянии Z от поверхности массива грунта. Точки по вертикали расположить от поверхности на расстоянии 1, 2, 4, 6 м. Точки по горизонтали расположить вправо и влево от оси действия силы P2 на расстоянии 0, 1, 3 м. По вычисленным напряжениям и заданным осям построить эпюры распределения напряжений sz. Исходные данные приведены в Таблице 4. Схема к расчету представлена на Рисунке 1.
Таблица 4 - Исходные данные к Задаче № 2
| Номер варианта | P1, кН | P2, кН | P3, кН | r1, м | r2, м | Z, м |
| 2,5 1,5 2,5 |

Рисунок 1. Схема к расчету напряжений по задаче №2
Задача № 3. Горизонтальная поверхность массива грунта по прямоугольным плитам с размерами в плане а1 х b1 и а2 х b2 нагружена равномерно распределенной вертикальной нагрузкой интенсивностью P1 и P2. Определить величины вертикальных составляющих напряжений sz от совместного действия внешних нагрузок в точках массива грунта для заданной вертикали, проходящей через одну из точек M1, M2, М3 на плите № I. Расстояние между осями плит нагружения L. Точки по вертикали расположить от поверхности на расстоянии 1, 2, 4 и 6 м. По вычисленным напряжениям построить эпюру распределения sz. Исходные данные приведены в Таблице 5. Схема к расчету представлена на Рисунке 2.
Таблица 5 - Исходные данные к Задаче № 3
| Номер варианта | а1, м | в1, м | а2, м | в2, м | Р1, МПа | Р2, МПа | L, м | Расчетная вертикаль |
| 2,5 3,3 2,9 2,6 2,5 2,2 1,9 2,5 2,7 5,0 | 1,9 2,3 2,6 2,1 1,9 2,2 1,9 2,1 1,9 2,4 | 3,3 4,0 3,5 5,0 6,0 3,0 2,9 4,0 3,5 6,0 | 2,3 2,4 2,5 2,4 2,8 2,4 2,6 2,4 2,5 2,4 | 0,28 0,24 0,32 0,34 0,29 0,26 0,28 0,31 0,32 0,38 | 0,31 0,35 0,29 0,38 0,33 0,36 0,32 0,41 0,34 0,32 | 2,8 3,3 3,5 3,0 2,8 3,0 3,2 3,4 3,2 4,0 | М1 М2 М3 М2 М3 М2 М1 М2 М3 М1 |

Рисунок 2. Схема к расчету напряжений по задаче №3
Задача № 4. К горизонтальной поверхности массива грунта приложена вертикальная неравномерная нагрузка, распределенная в пределах гибкой полосы (ширина полосы b) по закону трапеции от Р1 до Р2. Определить величины вертикальных составляющих напряжений sz в точках массива грунта для заданной вертикали, проходящей через одну из точек M1, M2, М3, M4, загруженной полосы, и горизонтали, расположенной на расстоянии Z от поверхности. Точки по вертикали расположить от поверхности на расстоянии 1, 2, 4, 6 м. Точки по горизонтали расположить вправо и влево от середины загруженной полосы на расстоянии 0, 1, 3 м. По вычисленным напряжениям построить эпюры распределения напряжений sz Исходные данные приведены в Таблице 6. Схема к расчету представлена на Рисунке 3.
Таблица 6 - Исходные данные к Задаче № 4
| Номер варианта | b, м | Р1, мПа | P2, мПа | Z, м | Расчетная вертикаль |
| 0,12 0,18 0,22 0,26 0,14 0,16 0,24 0,15 0,13 0,21 | 0,22 0,28 0,32 0,36 0,24 0,26 0,34 0,25 0,23 0,31 | М1 М2 М3 М4 М5 М5 М4 М3 М2 М1 |

Рисунок 3. Схема к расчету напряжений по задаче №4
Задача № 5. Откосы котлована глубиной Н проектируются с заложением m. Грунт в состоянии природной влажности имеет следующие характеристики физико-механических свойств: объёмный вес грунта γ, угол внутреннего трения j, удельное сцепление с. Определить методом кругло-цилиндрических поверхностей скольжения величину коэффициента устойчивости откоса. Исходные данные приведены в Таблице 7. Схема к расчету представлена на Рисунке 4.
Таблица 7 - Исходные данные к Задаче № 5
| Номер варианта | H, м | m | γ, кН/ м3 | φ,град | с, МПа |
| 1,5 1,5 2,0 2,0 1,5 2,0 1,5 1,5 2,0 1,5 | 19,4 20,5 19,6 20,8 19,7 20,1 20,3 19,8 19,7 19,1 | 0,018 0,021 0,016 0,025 0,051 0,047 0,041 0,023 0,019 0,015 |

Рисунок 4. Схема к расчету по задаче №5
Задача № 6. Подпорная стенка высотой Н с абсолютно гладкими вертикальными гранями и горизонтальной поверхностью засыпки грунта за стенкой имеет заглубление фундамента hзагл и ширину подошвы фундамента b. Засыпка за стенкой и основание представлены глинистым грунтом, имеющим следующие характеристики физико-механических свойств: объёмный вес грунта γ, угол внутреннего трения j, удельное сцепление с. Требуется определить: а) аналитическим методом величины равнодействующих активного и пассивного давлений грунта на подпорную стенку без учета нагрузки на поверхности засыпки, построить эпюры активного и пассивного давлений грунта, указать направления и точки приложения равнодействующих давления грунте; б) графическим методом, предложенным Ш. Кулоном, величину максимального давления грунта на заднюю грань подпорной стенки при наличии на поверхности засыпки равномерно распределенной нагрузки интенсивностью q. Исходные данные приведены в Таблице 8. Схема к расчету представлена на Рисунке 5.
Таблица 8 - Исходные данные к Задаче № 6
| Номер варианта | H, м | hзагл, м | В, м | γ, кН/ м3 | φ, град | с, МПа | g, МПа |
| 1,8 2,2 2,0 1,9 2,5 1,6 1,9 3,2 2,3 2,4 | 2,8 3,6 3,2 2,4 4,0 1,9 2,6 3,8 3,4 3,0 | 20,5 19,8 20,2 20,9 20,8 19,7 20,5 19,8 19,6 20,4 | 0,016 0,018 0,015 0,021 0,023 0,019 0,014 0,022 0,025 0,025 | 0,15 0,22 0,16 0,15 0,18 0,12 0,24 0,25 0,15 0,14 |

Рисунок 5. Расчётная схема к задаче №6.
Задача №7. Равномерно распределенная полосообразная (ширина полосы b) нагрузка интенсивностью P приложена на глубине h от горизонтальной поверхности слоистой толщи грунтов. Определить по методу послойного суммирования с учетом только осевых сжимающих напряжений величину полной стабилизированной осадки грунтов. С поверхности залегает песчаный грунт (мощность h1, объёмный вес грунта γ1, плотность частиц грунта rs1, природная влажность W1, модуль общей деформации E01), подстилаемый водонепроницаемой глиной (h2, γ2, E02). Уровень грунтовых вод расположен в слое песчаного грунта на расстоянии hb от уровня подстилающего слоя. Исходные данные приведены в Таблице 9. Схема к расчету представлена на Рисунке 6.

Рисунок 6. Расчётная схема к задаче №7.
Таблица 9 - Исходные данные к Задаче № 7
| Номер вари- анта | b, м | h, м | Р, МПа | h1, м | γ1, кН/ м3 | γs1, кН/ м3 | W1, % | E01, МПа | h 2, м | γ2, кН/ м3 | E02, МПа | h b, м |
| 2,4 1,2 2,8 1,6 1,4 2,0 3,2 2,4 1,6 2,0 | 1,3 1,5 1,4 1,6 1,2 1,6 1,2 1,5 1,3 1,7 | 0,38 0,18 0,36 0,28 0,26 0,32 0,41 0,31 0,22 0,27 | 3,2 2,8 3,6 3,5 3,1 4,6 5,2 3,9 4,3 4,1 | 19,8 18,9 20,5 20,9 19,9 20,2 20,9 20,1 19,4 19,6 | 26,5 26,6 26,5 26,6 26,7 26,6 26,7 26,5 26,5 26,6 | 12,4 9,8 11,8 14,1 10,6 13,315,2 12,9 10,2 11,2 | 7,6 3,6 7,5 3,7 4,2 4,4 8,2 6,9 3,9 4,8 | 20,1 19,5 19,2 20,2 18,9 19,7 20,6 19,1 20,8 19,9 | 1,6 1,2 1,1 2,2 1,5 2,9 2,3 1,7 2,4 1,8 |
Задача №8. Равномерно распределенная в пределах прямоугольной площадки a x b нагрузка интенсивностью P приложена к слою суглинка (мощность h1, коэффициент относительной сжимаемости mv1, коэффициент фильтрации Кф1), подстилаемому глиной (h2, mv2, Кф2). Определить по методу эквивалентного слоя величину полной стабилизированной осадки грунтов, изменение осадки грунтов во времени в условиях одномерной задачи теории фильтрационной консолидации, построить график стабилизации осадки вида S=¦(t). Исходные данные приведены в Таблице 10. Схема к расчету представлена на Рисунке 7.
Таблица 10 - Исходные данные к Задаче № 8
| Номер вари- анта | а, м | b, м | Р, МПа | h1, м | Mv1, МПа-1 | Кф1, м/с | h 2, м | Mv2, МПа-1 | Кф2, м/с |
| 2,0 2,2 3,6 3,5 5,6 3,0 3,2 3,8 1,9 2,5 | 2,0 2,2 2,4 1,75 2,8 2,0 3,2 1,9 1,9 2,5 | 0,24 0,21 0,19 0,17 0,22 0,23 0,18 0,28 0,16 0,26 | 2,3 2,8 3,1 3,2 3,8 2,9 2,4 3,9 1,8 2,7 | 0,176 0,139 0,065 0,076 0,105 0,087 0,148 0,105 0,222 0,095 | 2,2*10-10 4,3*10-10 1,2*10-10 2,4*10-9 5,1*10-10 2,3*10-10 1,4*10-9 2,7*10-10 1,7*10-9 6,4*10-10 | 3,9 4,1 4,8 3,5 5,6 4,3 5,8 3,4 4,4 4,7 | 0,284 0,215 0,124 0,381 0,245 0,147 0,258 0,276 0,065 0,196 | 4,13*10-11 4,6*10-11 2,5*10-11 1,8*10-10 6,9*10-11 3,8*10-11 5,6*10-10 1,6*10-11 8,4*10-10 3,2*10-11 |
Примечание. При определении значения коэффициента эквивалентного слоя Awconst (для абсолютно жестких фундаментов) коэффициент относительной поперечной деформации для сжимаемой толщи грунтов можно принять n = 0,3.

Рисунок 7. Расчётная схема к задаче №8.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ РАБОТЫ
Задача №I. Для определения степени неоднородности гранулометрического состава песчаных грунтов строят интегральную кривую гранулометрического состава. При построении интегральной кривой гранулометрического состава грунта по оси абсцисс откладывают диаметры частиц в мм (для сокращения размеров графика по горизонтали рекомендуется логарифмический масштаб), а по оси ординат процентное содержание частиц нарастающим итогом. При этом суммирование начинают с самой мелкой фракции. Приемы построения такого графика приведены в литературе. Степень неоднородности гранулометрического состава U определяется по формуле
 ,
,
где d60, d10- диаметры частиц, меньше которых в данном грунте содержится соответственно 60 и 10 частиц по массе (принимаются по интегральной кривой гранулометрического состава грунта).
По заданному гранулометрическому составу можно определить тип грунта [2, Таблица 2]; [10, Таблица 1.5].
Важным показателем оценки свойств песчаных грунтов является плотность их сложения. Пески по плотности их сложения подразделяются в зависимости от величины коэффициента пористости в естественном состоянии на плотные, средней плотности и рыхлые [2, Таблица 2]; [10, Таблица 1.7]; [11, Таблица 1.2]. Величину коэффициента пористости L можно определить по формуле
 ,
,
где rs - плотность частиц грунта;
rd – плотность сухого грунта: 
r - плотность грунта;
W – природная влажность.
Разновидность песчаных грунтов по степени влажности Sr определяется согласно ГОСТ [2, Таблица 2].

где rw - плотность воды.
Тип глинистого грунта и разновидность по консистенции определяются по заданным границам текучести, раскатывания и природной влажности [2, Таблица 2]; [10, Таблица 1.8 и Таблица 1.9]; [11].
Расчетные сопротивления Ro песчаных и глинистых грунтов определяются на основании оценки их вида и состояния по заданным характеристикам физических свойств в соответствии с нормами проектирования [9, Таблица 2.3].
Для определения коэффициента относительной сжимаемости грунта необходимо прежде всего вычислить коэффициенты пористости грунта ei, соответствующие заданным ступеням нагрузки, по формуле

где ei - искомое значение коэффициента пористости грунта после
уплотнения под нагрузкой Pi;
e0 - начальное (до уплотнения) значение коэффициента пористости грунта;
Si - полная осадка образца грунта при заданной нагрузке Pi, измеренная от начала загружения;
h - начальная (до уплотнения) высота образца грунта. Коэффициент относительной сжимаемости грунта mv определяется по формуле
 ,
,
где mo - коэффициент сжимаемости грунта для заданного расчетного интервала давлений:
 ,
,
e1 и e2 - коэффициенты пористости, соответствующие давлениям P1 и Р2;
Р2-Р1=Р - заданный расчетный интервал давлений, или так называемое действующее давление.
Числовые значения коэффициента относительной сжимаемости mv позволяют судить о сжимаемости грунтов. При значениях mv порядка 1 МПа-1 - грунт сильносжимаемый; при mv порядка 0,1 МПа-1 - среднесжимаемый и при mv порядка 0,01 МПа-1 - малосжимаемый [l].
Модуль деформации вычисляют для заданного расчетного интервала давлений
Р= Р2 – Р1 по формуле
 ,
,
где e0 - начальный коэффициент пористости грунта;
b - коэффициент, учитывающий отсутствие поперечного расширения грунта в приборе и назначаемый в зависимости от коэффициента Пуассона n (Таблица 11).
Таблица 11

Для определения нормативного значения угла внутреннего трения jн следует воспользоваться формулами, составленными на основе законов математической статистики [6] и [10]:
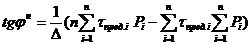 ,
,
где n - число экспериментов по определению сопротивления грунта сдвигу tпред.i при давлении рi;
∆ - общий знаменатель этого выражения, определяемый по формуле:
 .
.
Для определения удельного сцепления грунта сн воспользуйтесь формулой:
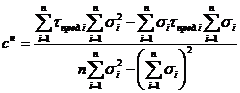
Примеры определения нормативных значений угла внутреннего трения jн и удельного сцепления сн, а так же построения графиков сдвига приведены в [4]; [8].
Задача №2. Для случая, когда к горизонтальной поверхности массива грунта приложено несколько сосредоточенных сил P1, P2, Р3…Pn, величины вертикальных составляющих напряжений σzi в любой, точке массива грунта можно определить суммированием составляющих напряжений от действия каждой силы в отдельности с использованием зависимости
 ,
,
где Ki - коэффициент, являющийся функцией отношения  ;
;
ri - расстояние по горизонтальной оси от рассматриваемой точки до оси Z, проходящей через точку приложения сосредоточенной силы Pi;
Zi - глубина рассматриваемой точки от плоскости приложения сосредоточенной силы Рi.
Значения коэффициента К (Ki) приведены в Приложении 1 данных указаний, а также в [I, Таблице 6 Приложения]; [3, Таблица 4.1]; [7, Таблица II]; [11, Таблица III.l]. При построении расчетной схемы и эпюр напряжений следует принимать масштаб расстояний 1:50, масштаб напряжений 0,05 МПа в I см. Примеры расчета приведены в [7]; [11].
Задача №3. Распределение по глубине вертикальных составляющих напряжений σzc в любой точке массива грунта от действия равномерно распределенной нагрузки в пределах или за пределами плит нагружения может быть определено по методу угловых точек по формуле
σzc = КсР,
где Кс - коэффициент, определяемый в зависимости от отношения сторон прямоугольной площади загружения a/b (а - длинная ее сторона, b - ее ширина) и отношения Z/b (Z - глубина, на которой определяется напряжение σzc);
P - интенсивность равномерно распределенной нагрузки.
В соответствии с этим заданные плиты нагружения разбивают на прямоугольники таким образом, чтобы они имели общую угловую точку, через которую проходит расчетная вертикаль Mi. Для каждого из этих прямоугольников со сторонами аi  bi, с помощью таблиц определяют значения коэффициента Kсi и, пользуясь принципом независимости действия сил, находят алгебраическим суммированием напряжения в заданных точках массива грунта. Значения коэффициента Кс приведены в Приложении 1 данных указаний, а также в учебнике [11, Таблица III.5]. Масштаб расстояния 1:50, масштаб напряжений 0,05 МПа в I см. Примеры расчета приведены в [4]; [7]; [11].
bi, с помощью таблиц определяют значения коэффициента Kсi и, пользуясь принципом независимости действия сил, находят алгебраическим суммированием напряжения в заданных точках массива грунта. Значения коэффициента Кс приведены в Приложении 1 данных указаний, а также в учебнике [11, Таблица III.5]. Масштаб расстояния 1:50, масштаб напряжений 0,05 МПа в I см. Примеры расчета приведены в [4]; [7]; [11].
Задача № 4. Для случая действия на поверхности массива грунта нагрузки, распределенной в пределах гибкой полосы по трапецеидальной эпюре, величину вертикального сжимающего напряжения в заданной точке массива грунта определяют путем суммирования напряжений от прямо- и треугольного элементов эпюры внешней нагрузки.
Вертикальные напряжения σz, возникающие от действия полосообразной равномерно распределенной нагрузки (прямоугольный элемент эпюры внешней нагрузки), определяют по формуле
σz =КzP,
где Кz - коэффициент, определяемый в зависимости от величины относительных координат  и
и 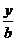 , приведен в Приложении 1 данных указаний, а также в [1, Таблице 4 Приложения]; [11, Таблица III.6];
, приведен в Приложении 1 данных указаний, а также в [1, Таблице 4 Приложения]; [11, Таблица III.6];
Р - вертикальная равномерно распределенная нагрузка.
Вертикальные напряжения σz, возникающие от действия полосообразной неравномерной нагрузки, распределенной по закону треугольника (треугольный элемент эпюры внешней нагрузки), определяются по формуле
 ,
,
где Кz - коэффициент, определяемый в зависимости от величины относительных координат  и
и 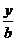 , приведен в Приложении 1 данных указаний, а также в [I, Таблица 5 Приложения]; [11, Таблица III. 7];
, приведен в Приложении 1 данных указаний, а также в [I, Таблица 5 Приложения]; [11, Таблица III. 7];
Р – наибольшая ордината треугольной нагрузки.
При построении расчетной схемы и эпюр напряжений следует принимать масштаб расстояний 1:50, масштаб напряжений 0,05 МПа в 1 см.
Примеры расчета приведены в [1]; [l4].
Задача. № 5. В проектной практике широко распространен расчет устойчивости откосов по методу круглоцилиндрических поверхностей скольжения. Проверка устойчивости откоса сводится к простейшим построениям по схеме, представленной на Рисунке 8. За коэффициент устойчивости откоса h принимают отношение момента сил, удерживающих откос от сдвига, Муд к моменту сил, стремящихся сдвинуть откос, Мсдв:
 ,
,
где n - число отсеков, на которые делится призма скольжения;
Ni - нормальные составляющие от веса отсеков Pi, равные Pi cosqi
Pi - вес расчетного отсека;
qi - угол между направлением силы Pi и нормальной составляющей Ni;
j - угол внутреннего трения;
C - удельное сцепление;
L - длина дуги скольжения;
R - радиус круглоцилиндрической дуги скольжения;
Ti - касательные составляющие от веса отсеков Pi, равные Pi sinqi
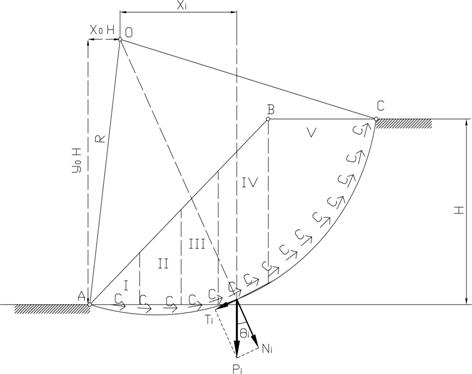
Рисунок 8. Расчётная схема к методу круглоцилиндрических поверхностей скольжения.
Для откосов в однородной толще грунтов весьма полезным для определения координат центра О(X, У) наиболее опасной круглоцилиндрической поверхности скольжения, для которой коэффициент устойчивости получается минимальным, является график Янбу, представленный на Рисунке 9 [4]:

Рисунок 9. График Янбу.
x = x0H; у = y0Н,
где Н - высота откоса;
x0, y0- безразмерные величины, устанавливаемые по графику Янбу в зависимости от угля откоса - a, (определяется по заданному заложению откоса m) и lср:

Вместе с тем, без большой погрешности около 10% в сторону завышения коэффициента запаса, принимая cosqi = 1, формула для определения коэффициента устойчивости откоса может быть записана в более простом виде [4]:
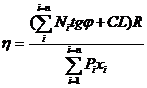 ,
,
где xi - плечо от линии действия веса расчетного отсека до центра вращения (см.рис.8).
Момент принимается для восходящей ветви кривой скольжения - отрицательным, для нисходящей - положительным.
Радиус круглоцилиндрической дуги скольжения R, а также ширину и высоту отсеков допускается определять графически с расчетной схемы, выполняемой в масштабе 1:100. Для расчета выделяют I пог.м по длине откоса (перпендикулярно к плоскости чертежа). Вес расчетного отсека определяется как произведение плотности грунта на объем отсека. Примеры расчета приведены в [4].
Задача №6. Определение давления грунта на вертикальную гладкую подпорную стенку с учетом внутреннего трения и сцепления грунта можно произвести по следующим зависимостям:
активное давление грунта σ2z в любой точке стенки:
 ;
;
где g - объёмный вес грунта, определяемый по формуле g=r×g;
r - плотность грунта;
g - ускорение свободного падения, равное 9,81 м/с2, часто принимают g = 10 м/с2;
Z- расстояние точки от поверхности засыпки;
пассивное давление σп в любой точке стенки:
 ;
;
равнодействующая Еа активного давления грунта:
 ,
,
где Н - высота подпорной стенки;
равнодействующая Еп пассивного давления грунта:
 ;
;
где hзагл - заглубление фундамента подпорной стенки.
Точка приложения Еа находится от подошвы фундамента подпорной стенки на расстоянии:
 ,
,
где hc- высота верхней части стенки, не воспринимающей давления
грунта;

Точка приложения Еп находится на высоте еп от подошвы фундамента подпорной стенки:
 ,
,
где а - величина пассивного давления грунта в уровне подошвы фундамента при Z = hзагл;
d - величина пассивного давления грунта в уровне обреза фундамента при Z = 0.
При построении расчетной схемы и эпюр активного и пассивного давлений грунта на подпорную стенку следует принимать масштаб расстояний 1:50, масштаб давлений 0,025 МПа в I см. Примеры расчета приведены в [4]; [6].
Для определения давления грунта на подпорную стенку графическим методом можно использовать построения, предложенные Ш. Кулоном. Последовательность такого определения приведена в [3] и [11].
Действие сплошной равномерно распределенной пригрузки горизонтальной поверхности засыпки грунта в этом случае заменяется эквивалентной высотой слоя грунта, равной:
 .
.
Масштаб расстояний для графического определения следует принять 1:50.
Задача №7. Величину полной стабилизированной осадки грунтовой толщи S по методу послойного суммирования определяют как сумму осадок элементарных слоев грунта по формуле

где  - безразмерный коэффициент, равный 0,8;
- безразмерный коэффициент, равный 0,8;
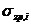 - среднее значение дополнительного вертикального нормального напряжения в i-м слое грунта, равное полусумме указанных напряжений на верхний Zi-1 и нижней Zi границах слоя по вертикали, проходящей через середину полосы нагружения;
- среднее значение дополнительного вертикального нормального напряжения в i-м слое грунта, равное полусумме указанных напряжений на верхний Zi-1 и нижней Zi границах слоя по вертикали, проходящей через середину полосы нагружения;
hi, Ei - соответственно толщина и модуль деформации i-го слоя грунта;
n - число элементарных слоев грунта, на которое разбита сжимаемая толща основания.
Дополнительные вертикальные напряжения szp определяются по формуле
szp=aP0,
где a - коэффициент, принимаемый в зависимости от относительной глубины, равной x=  ; а для ленточного фундамента h³10;
; а для ленточного фундамента h³10;
Ро - дополнительное вертикальное давление на основание;
Ро=P-szg,о,
Р - интенсивность полосообразной нагрузки;
szp,о - вертикальное напряжение от собственного веса грунта на уровне подошвы полосы нагружения.
Значения коэффициента a приведены в Приложении 1 данных указаний, а также в [l, табл.1 приложения]; [3 табл.4.2]; [9, табл.1 прил.2]. Нижняя граница сжимаемой толщи основания принимается на глубине Z = Нс, где выполняется условие szp=0,2szg.
При построении расчетной схемы следует принимать масштаб расстояний 1:50, масштаб напряжений 0,05 МПа в I см. Примеры расчета приведены в [I]; [6]; [7]; [8]; [10]; [11].
Задача № 8. При слоистой толще грунтов для расчета осадки по методу эквивалентного слоя грунт приводится к квазиоднородному (на основе теорем о среднем коэффициенте относительной сжимаемости и о среднем коэффициенте фильтрации). В этом случае величина полной стабилизированной осадки S может быть определена по формуле
S=hэ∙mvm∙P,
где hэ - толщина эквивалентного слоя грунта;
mvm - средний коэффициент относительной сжимаемости грунта;
Р - давление на грунт по подошве площадки.
Толщина эквивалентного слоя грунта hэ определяется по формуле
hэ=Аw∙b
где Аw - коэффициент эквивалентного слоя грунта, принимаемый для абсолютного жесткого фундамента по [3, Таблица 5.2]; [11, Таблица V.6], приведен в Приложении 1 данных указаний;
b - наименьшая сторона площадки нагружения.
Средний коэффициент относительной сжимаемости mvm определяется по формуле
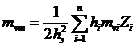 ,
,
где hi - толщина отдельных слоев грунта до глубины Н = 2hэ;
mvi - коэффициент относительной сжимаемости i-го слоя грунта;
Zi - расстояние от точки, соответствующей глубине Н, до середины
рассматриваемого i-го слоя грунта.
Осадка грунтовой толщи St для любого промежутка времени t определяется следующим выражением
St=S∙U,
где S - полная стабилизированная осадка;
U - степень консолидации (уплотнения).
Вычисление степени консолидации U можно с достаточной для практических целей точностью выполнять по формуле
 ,
,
где е - основание натуральных логарифмов;
N - коэффициент, зависящий от условий отвода вытесняемой из грунта воды;
 ,
,
Cvm - коэффициент консолидации, в данном случае
 ,
,
Kфт - средний коэффициент фильтрации:
 ,
,
Kфi - коэффициент фильтрации i-го слоя грунта;
rw - плотность воды.
Задаваясь той или иной степенью консолидации (например, U =0,1; 0,2; 0,3 и т.д.), принимают по [3, Таблица 5.б]; [11, Таблица V.4] соответствующие значения коэффициента N (для случая убывания давлений с глубиной по треугольной эпюре), также значения коэффициента N приведены в Приложении 1 данных указаний. Используя зависимость для N, определяют время t, соответствующее данной степени фильтрационной консолидации:
 .
.
При подсчете значения коэффициента консолидации Cvm коэффициент фильтрации Kф удобнее выражать в см/год (I см/с = 3-107 см/год). По результатам определений строится график изменения осадки грунтов во времени. Примеры расчета приведены в [6]; [11].
ПРИЛОЖЕНИЕ 1. ТАБЛИЦЫ ЗНАЧЕНИЙ НЕКОТОРЫХ ВЕЛИЧИН
К ВЫПОЛНЕНИЮ РАБОТЫ.
к задаче №2:

| к задаче №3: принимаем α=l/b как α=a/b | 
|
| к задаче №3: принимаем α=l/b как α=a/b |

|
к задаче №3: принимаем α=l/b как α=a/b

к задаче №4:

| к задаче №4: |

|
к задаче №7:
Коэффициент a
| x = 2 z / b | Коэффициент a для фундаментов | |||||||
| круглых | прямоугольных с соотношением сторон h = l / b, равным | ленточных (h ³ 10) | ||||||
| 1,0 | 1,4 | 1,8 | 2,4 | 3,2 | ||||
| 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | |
| 0,4 | 0,949 | 0,960 | 0,972 | 0,975 | 0,976 | 0,977 | 0,977 | 0,977 |
| 0,8 | 0,756 | 0,800 | 0,848 | 0,866 | 0,876 | 0,879 | 0,881 | 0,881 |
| 1,2 | 0,547 | 0,606 | 0,682 | 0,717 | 0,739 | 0,749 | 0,754 | 0,755 |
| 1,6 | 0,390 | 0,449 | 0,532 | 0,578 | 0,612 | 0,629 | 0,639 | 0,642 |
| 2,0 | 0,285 | 0,336 | 0,414 | 0,463 | 0,505 | 0,530 | 0,545 | 0,550 |
| 2,4 | 0,214 | 0,257 | 0,325 | 0,374 | 0,419 | 0,449 | 0,470 | 0,477 |
| 2,8 | 0,165 | 0,201 | 0,260 | 0,304 | 0,349 | 0,383 | 0,410 | 0,420 |
| 3,2 | 0,130 | 0,160 | 0,210 | 0,251 | 0,294 | 0,329 | 0,360 | 0,374 |
| 3,6 | 0,106 | 0,131 | 0,173 | 0,209 | 0,250 | 0,285 | 0,319 | 0,337 |
| 4,0 | 0,087 | 0,108 | 0,145 | 0,176 | 0,214 | 0,248 | 0,285 | 0,306 |
| 4,4 | 0,073 | 0,091 | 0,123 | 0,150 | 0,185 | 0,218 | 0,255 | 0,280 |
| 4,8 | 0,062 | 0,077 | 0,105 | 0,130 | 0,161 | 0,192 | 0,230 | 0,258 |
| 5,2 | 0,053 | 0,067 | 0,091 | 0,113 | 0,141 | 0,170 | 0,208 | 0,239 |
| 5,6 | 0,046 | 0,058 | 0,079 | 0,099 | 0,124 | 0,152 | 0,189 | 0,223 |
| 6,0 | 0,040 | 0,051 | 0,070 | 0,087 | 0,110 | 0,136 | 0,173 | 0,208 |
| 6,4 | 0,036 | 0,045 | 0,062 | 0,077 | 0,099 | 0,122 | 0,158 | 0,196 |
| 6,8 | 0,031 | 0,040 | 0,055 | 0,064 | 0,088 | 0,110 | 0,145 | 0,185 |
| 7,2 | 0,028 | 0,036 | 0,049 | 0,062 | 0,080 | 0,100 | 0,133 | 0,175 |
| 7,6 | 0,024 | 0,032 | 0,044 | 0,056 | 0,072 | 0,091 | 0,123 | 0,166 |
| 8,0 | 0,022 | 0,029 | 0,040 | 0,051 | 0,066 | 0,084 | 0,113 | 0,158 |
| 8,4 | 0,021 | 0,026 | 0,037 | 0,046 | 0,060 | 0,077 | 0,105 | 0,150 |
| 8,8 | 0,019 | 0,024 | 0,033 | 0,042 | 0,055 | 0,071 | 0,098 | 0,143 |
| 9,2 | 0,017 | 0,022 | 0,031 | 0,039 | 0,051 | 0,065 | 0,091 | 0,137 |
| 9,6 | 0,016 | 0,020 | 0,028 | 0,036 | 0,047 | 0,060 | 0,085 | 0,132 |
| 10,0 | 0,015 | 0,019 | 0,026 | 0,033 | 0,043 | 0,056 | 0,079 | 0,126 |
| 10,4 | 0,014 | 0,017 | 0,024 | 0,031 | 0,040 | 0,052 | 0,074 | 0,122 |
| 10,8 | 0,013 | 0,016 | 0,022 | 0,029 | 0,037 | 0,049 | 0,069 | 0,117 |
| 11,2 | 0,012 | 0,015 | 0,021 | 0,027 | 0,035 | 0,045 | 0,065 | 0,113 |
| 11,6 | 0,011 | 0,014 | 0,020 | 0,025 | 0,033 | 0,042 | 0,061 | 0,109 |
| 12,0 | 0,010 | 0,013 | 0,018 | 0,023 | 0,031 | 0,040 | 0,058 | 0,106 |
Примечания:
1. В табл. 1 обозначено: b - ширина или диаметр фундамента, l - длина фундамента.
2. Для фундаментов, имеющих подошву в форме правильного многоугольника с площадью А, значения a принимаются как для круглых фундаментов радиусом
к задаче №8:

| к задаче №8: | 
|
ЛИТЕРАТУРА
1. Веселов В. А. Проектирование оснований и фундаментов (основы теории и примеры расчета). – М.: Стройиздат, 1990. – 210с.
2. ГОСТ 25100-95. Грунты. Классификация.
3. Далматов В. И. Механика грунтов, основания и фундаменты. – М.: Стройиздат, 1981. – 310 с.
4. Котов М. Ф. Механика грунтов в примерах. – М.: Высшая школа, 1968. – 271 с.
5. Маслов Н. Н. Механика грунтов в практике строительства. – М.: Стройиздат, 1977. – 314 с.
6. Мулин В. И. Механика грунтов для инженеров-строителей. – М.: Стройиздат, 1978. – 113 с.
7. Пешковский Л. М. Расчеты оснований и фундаментов гражданских и промышленных зданий. – М.: Высшая школа, 1968. – 277 с.
8. Пособие по проектированию оснований зданий и сооружений (к СНиП 2.02.01-83). – М.: Стройиздат, 1986. – 415 с.
9. СНиП 2.02.01-83. Основания зданий и сооружений.
10. Справочник проектировщика. Основания, фундаменты и подземные сооружения / Под общей ред. Е. А. Сорочана и Ю. Г. Трофименкова. – М.: Стройиздат, 1985. – 479 с.
11. Цытович Н. А. Механика грунтов (краткий курс). – М.: Высшая школа, 1983. – 280 с.
12. Берлинов М. В. Основания и фундаменты. – М.: АСТ, 2002.
13. Основания и фундаменты: Справочник под ред. Г. И. Швецова. – М.: Стройиздат, 1991.
| <== предыдущая лекция | | | следующая лекция ==> |
| | | СТРУКТУРА УЧЕБНОЙ ДИСЦИПЛИНЫ |
Не нашли, что искали? Воспользуйтесь поиском: