
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Теоретические упражнения
III. ГРАФИКИ
Теоретические вопросы
1. Условия возрастания функции на отрезке.
2. Условия убывания функции на отрезке.
3. Точки экстремума. Необходимое условие экстремума.
4. Достаточные признаки максимума и минимума функции (изменение знака первой производной).
5. Наибольшее и наименьшее значения, функции, непрерывной на отрезке.
6. Выпуклость и вогнутость графика функции. Достаточные условия выпуклости и вогнутости.
7. Точки перегиба графика функции. Необходимое условие перегиба. Достаточные условия перегиба.
8. Исследование функций на экстремум с помощью высших производных.
9. Асимптоты графика функции.
Теоретические упражнения
1. Доказать, что функция  монотонно возрастает на отрезке: а)
монотонно возрастает на отрезке: а)  ; б)
; б)  Следует ли из монотонности дифференцируемой функции монотонность ее производной?
Следует ли из монотонности дифференцируемой функции монотонность ее производной?
2. Доказать теорему: если функции  и
и 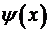 дифференцируемы на отрезке
дифференцируемы на отрезке 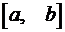 и
и 
 , а
, а  , то
, то 
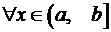 .
.
Дать геометрическую интерпретацию теоремы.
У к а з а н и е. При доказательстве теоремы установить и использовать монотонность функции  .
.
3. Доказать неравенство 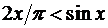 для трех случаев:
для трех случаев:
а)  ;
;
б) 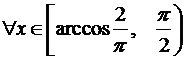 ;
;
в )  .
.
Дать геометрическую интерпретацию неравенства.
4. Исходя из определений минимума и максимума, доказать, что функция

имеет в точке  минимум, а функция
минимум, а функция

не имеет в точке  экстремума.
экстремума.
5. Исследовать на экстремум в точке  функцию
функцию  , считая, что производная
, считая, что производная 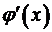 не существует, но функция
не существует, но функция  непрерывна в точке
непрерывна в точке  и
и  ,
, 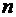 .— натуральное число.
.— натуральное число.
6. Исследовать знаки максимума и минимума функции  и выяснить условия, при которых уравнение
и выяснить условия, при которых уравнение 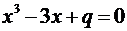 имеет а) три различных действительных корня; б) один действительный корень.
имеет а) три различных действительных корня; б) один действительный корень.
7. Определить «отклонение от нуля» многочлена  на отрезке
на отрезке  , т. е. найти на этом отрезке наибольшее значение функции
, т. е. найти на этом отрезке наибольшее значение функции 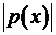 .
.
8. Установить условия существования асимптот у графика рациональной функции.
Расчетные задания
Задача 1. Построить графики функций с помощью производной первого порядка.
1.1.  1.2.
1.2. 
1.3.  1.4.
1.4. 
1.5.  1.6.
1.6. 
1.7. 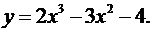 1.8.
1.8. 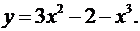
1.9. 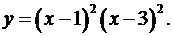 1.10.
1.10. 
1.11.  1.12.
1.12. 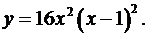
1.13.  1.14.
1.14. 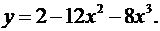
1.15. 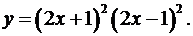 1.16.
1.16. 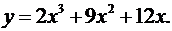
1.17.  1.18.
1.18. 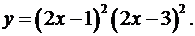
1.19.  1.20.
1.20. 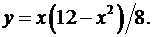
1.21.  1.22.
1.22. 
1.23.  1.24.
1.24. 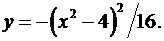
1.25.  1.26.
1.26. 
1.27. 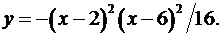 1.28.
1.28. 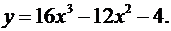
1.29.  1.30.
1.30. 
1.31. 
Задача 2. Построить графики функций с помощью производной первого порядка.
2.1. 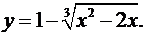 2.2.
2.2. 
2.3.  2.4.
2.4. 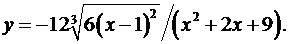
2.5.  2.6.
2.6. 
2.7.  2.8.
2.8. 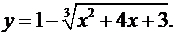
2.9.  2.10.
2.10. 
2.11.  2.12.
2.12. 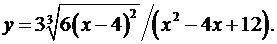
2.13.  2.14.
2.14. 
2.15.  2.16.
2.16. 
2.17.  2.18.
2.18. 
2.19.  2.20.
2.20. 
2.21.  2.22.
2.22. 
2.23. 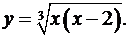 2.24.
2.24. 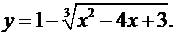
2.25.  2.26.
2.26. 
2.27.  2.28.
2.28. 
2.29.  2.30.
2.30. 
2.31. 
Задача 3. Найти наибольшее и наименьшее значения функций на заданных отрезках.
3.1. 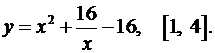 3.2.
3.2. 
3.3.  3.4.
3.4. 
3.5.  3.6.
3.6. 
3.7.  3.8.
3.8. 
3.9.  3.10.
3.10. 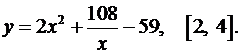
3.11.  3.12.
3.12. 
3.13.  3.14.
3.14. 
3.15.  3.16.
3.16. 
3.17.  3.18.
3.18. 
3.19.  3.20.
3.20. 
3.21. 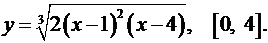 3.22.
3.22. 
3.23. 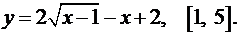 3.24.
3.24. 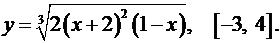
3.25.  3.26.
3.26. 
3.27.  3.28.
3.28. 
3.29. 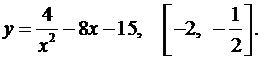 3.30.
3.30. 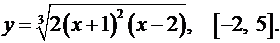
3.31. 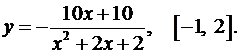
Задача 4.
 Варианты 1 – 10.
Варианты 1 – 10.
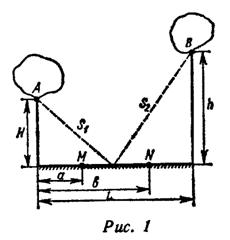
Рыбаку нужно переправиться с острова  на остров
на остров 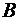 (рис. 1). Чтобы пополнить свои запасы, он должен попасть на участок берега
(рис. 1). Чтобы пополнить свои запасы, он должен попасть на участок берега  . Найти кратчайший путь рыбака
. Найти кратчайший путь рыбака 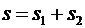 .
.
4.1. 
4.2. 
4.3. 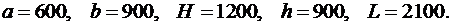
4.4. 
4.5. 
4.6. 
4.7. 
4.8. 
4.9. 
4.10. 
Варианты 11 – 20.
При подготовке к экзамену студент за  дней изучает
дней изучает 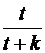 -ю часть курса, а забывает
-ю часть курса, а забывает  -ю часть. Сколько дней нужно затратить на подготовку, чтобы была изучена максимальная часть курса?
-ю часть. Сколько дней нужно затратить на подготовку, чтобы была изучена максимальная часть курса?
4.11.  4.12.
4.12. 
4.13.  4.14.
4.14. 
4.15.  4.16.
4.16. 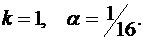
4.17. 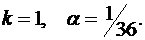 4.18.
4.18. 
4.19.  4.20.
4.20. 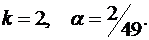
Варианты 21 – 31.
Тело массой 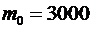 кг падает с высоты
кг падает с высоты  м и теряет массу (сгорает) пропорционально времени падения. Коэффициент пропорциональности
м и теряет массу (сгорает) пропорционально времени падения. Коэффициент пропорциональности  кг/с2. Считая, что начальная скорость
кг/с2. Считая, что начальная скорость  , ускорение
, ускорение  м/с2, и пренебрегая сопротивлением воздуха найти наибольшую кинетическую энергию тела.
м/с2, и пренебрегая сопротивлением воздуха найти наибольшую кинетическую энергию тела.
4.21.  4.22.
4.22.  4.23.
4.23. 
4.24. 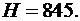 4.25.
4.25.  4.26.
4.26. 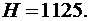
4.27. 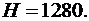 4.28.
4.28. 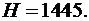 4.29.
4.29. 
4.30.  4.31.
4.31. 
Задача 5. Исследовать поведение функций в окрестностях заданных точек с помощью производных высших порядков.
5.1. 
5.2. 
5.3. 
5.4. 
5.5. 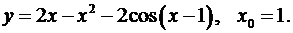
5.6. 
5.7. 
5.8. 
5.9. 
5.10. 
5.11. 
5.12. 
5.13. 
5.14. 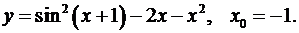
5.15. 
5.16. 
5.17. 
5.18. 
5.19. 
5.20. 
5.21. 
5.22. 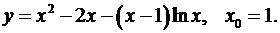
5.23. 
5.24. 
5.25. 
5.26. 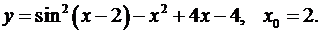
5.27. 
5.28. 
5.29. 
5.30. 
5.31. 
Задача 6. Найти асимптоты и построить графики функций.
6.1.  6.2.
6.2. 
6.3.  6.4.
6.4. 
6.5.  6.6.
6.6. 
6.7.  6.8.
6.8. 
6.9. 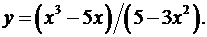 6.10.
6.10. 
6.11.  6.12.
6.12. 
6.13.  6.14.
6.14. 
6.15.  6.16.
6.16. 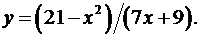
6.17.  6.18.
6.18. 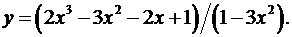
6.19. 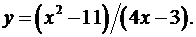 6.20.
6.20. 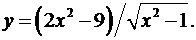
6.21.  6.22.
6.22. 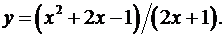
6.23.  6.24.
6.24. 
6.25. 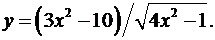 6.26.
6.26. 
6.27.  6.28.
6.28. 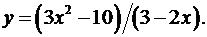
6.29.  6.30.
6.30. 
6.31. 
Задача 7. Провести полное исследование функций и построить их графики.
7.1.  7.2.
7.2. 
7.3.  7.4.
7.4. 
7.5.  7.6.
7.6. 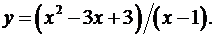
7.7.  7.8.
7.8. 
7.9.  7.10.
7.10. 
7.11. 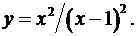 7.12.
7.12. 
7.13.  7.14.
7.14. 
7.15.  7.16.
7.16. 
7.17.  7.18.
7.18. 
7.19.  7.20.
7.20. 
7.21. 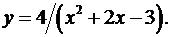 7.22.
7.22. 
7.23.  7.24.
7.24. 
7.25.  7.26.
7.26. 
7.27.  7.28.
7.28. 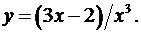
7.29.  7.30.
7.30. 
7.31. 
Задача 8. Провести полное исследование функций и построить их графики.
8.1. 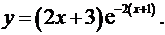 8.2.
8.2. 
8.3.  8.4.
8.4. 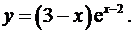
8.5. 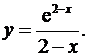 8.6.
8.6. 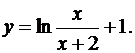
8.7.  8.8.
8.8. 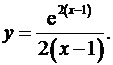
8.9.  8.10.
8.10. 
8.11.  8.12.
8.12. 
8.13.  8.14.
8.14. 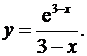
8.15. 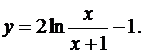 8.16.
8.16. 
8.17.  8.18.
8.18. 
8.19.  8.20.
8.20. 
8.21.  8.22.
8.22. 
8.23. 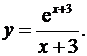 8.24.
8.24. 
8.25.  8.26.
8.26. 
8.27.  8.28.
8.28. 
8.29.  8.30.
8.30. 
8.31. 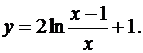
Задача 9. Провести полное исследование функций и построить их графики.
9.1.  9.2.
9.2. 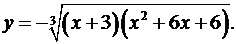
9.3.  9.4.
9.4. 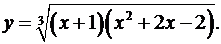
9.5.  9.6.
9.6. 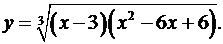
9.7.  9.8.
9.8. 
9.9.  9.10.
9.10. 
9.11. 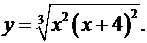 9.12.
9.12. 
9.13.  9.14.
9.14. 
9.15.  9.16.
9.16. 
9.17. 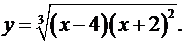 9.18.
9.18. 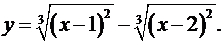
9.19.  9.20.
9.20. 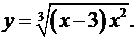
9.21.  9.22.
9.22. 
9.23.  9.24.
9.24. 
9.25.  9.26.
9.26. 
9.27. 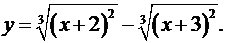 9.28.
9.28. 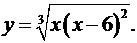
9.29.  9.30.
9.30. 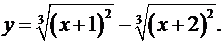
9.31. 
Задача 10. Провести полное исследование функций и построить их графики.
10.1.  10.2.
10.2. 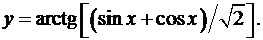
10.3.  10.4.
10.4. 
10.5. 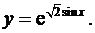 10.6.
10.6. 
10.7.  10.8.
10.8. 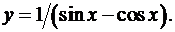
10.9.  10.10.
10.10. 
10.11.  10.12.
10.12. 
10.13.  10.14.
10.14. 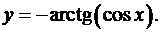
10.15.  10.16.
10.16. 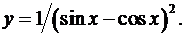
10.17. 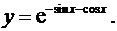 10.18.
10.18. 
10.19.  10.20.
10.20. 
10.21.  10.22.
10.22. 
10.23.  10.24.
10.24. 
10.25.  10.26.
10.26. 
10.27. 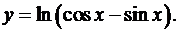 10.28.
10.28. 
10.29. 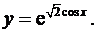 10.30.
10.30. 
10.31. 
| <== предыдущая лекция | | | следующая лекция ==> |
| Программа выступления коллективов | | |
Не нашли, что искали? Воспользуйтесь поиском: