Алгебраические свойства циклических кодов

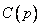При работе с циклическими кодами принято связывать с кодовым словом полином степени 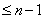, определённый так

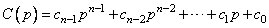. (1.1)

Для двоичного кода каждый из коэффициентов полинома является или нулем, или единицей. Рассмотрим алгебру циклических кодов. Допустим, необходимо перемножить три многочлена (x³+x²+1)·(x³+x+1)·(x+1). Действия производятся также как в обычной алгебре, только сложение проводится по модулю 2.

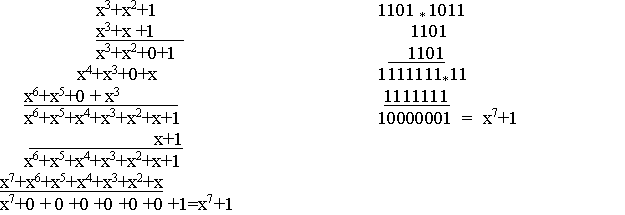
При делении операция вычитания заменяется операцией сложения по модулю 2. Например, необходимо разделить многочлен седьмой степени на многочлен третей степени (x⁷+x⁵+x⁴+x+1) / (x³+x²+1)

Операция деления может быть произведена или в виде многочленов или в виде двоичных кодов.

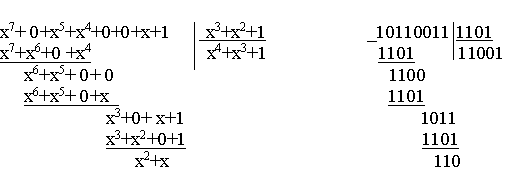
Схема деления реализуется на регистрах сдвига со встроенными сумматорами по модулю 2. Вид схемы определяется многочленом, на который производится деление. В процессе деления с помощью такого устройства находится остаток.

Теперь предположим, мы формируем полином

.

Этот полином не может представить кодовое слово, так как его степень может быть равна 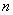(если 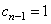). Однако если мы разделим 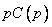на , мы получим

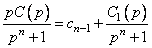, (1.2)

где

.

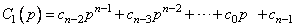Заметим, что полином представляет кодовое слово , которое как раз образовано из кодового слова циклическим сдвигом на одну позицию. Поскольку представляет собой остаток, полученный делением 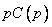на , мы говорим, что

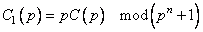. (1.3)

Аналогичным образом, если 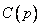представляет кодовое слово в циклическом коде, тогда 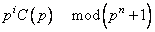также является кодовым словом циклического кода. Так что можно написать

, (1.4)

где остаточный полином 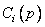представляет кодовое слово циклического кода, a -частное.

Мы можем генерировать циклический 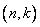код, используя порождающий полином степени с двоичными коэффициентами, который является множителем при факторизации полинома . Порождающий полином в общем виде можно записать так

. (1.5)

Мы также определяем полином информационного сообщения

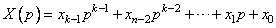, (1.6)

где 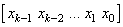определяет 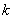информационных бит. Ясно, что произведение 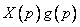- это полином степени меньшей или равной 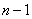, который может представлять кодовое слово. Заметим, что имеется 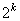полиномов 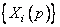и, следовательно, имеется 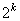возможных кодовых слов, которые можно формировать при заданном .

Допустим, что мы обозначим эти кодовые слова так

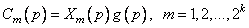(1.7)

Чтобы показать, что кодовые слова в (1.7) удовлетворяют циклическому сдвигу, рассмотрим какое-либо кодовое слово 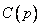в (1.7), Циклический сдвиг 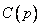дает

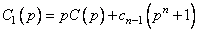(1.8)

и, поскольку и и 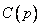делятся на без остатка, то и делится на без остатка, т.е. можно представить как

.

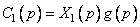Следовательно, циклический сдвиг в кодовом слове 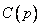, генерируемый согласно (1.7), порождает другое кодовое слово.

Из вышесказанного мы видим, что кодовые слова, обладающие циклическими свойствами, можно генерировать умножением 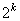сообщений на уникальный полином степени - называемый порождающим полиномом циклического 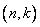кода, который является множителем при факторизации . Циклический код, генерируемый указанным образом, занимает подпространство 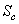векторного пространства . Размерность подпространств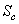а равна .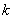

Пример 1.1 Рассмотрим код с длиной блока 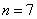. Полином можно разложить на следующие сомножители

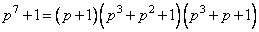. (1.9)

Чтобы синтезировать циклический код (7,4), мы можем взять один из двух порождающих полиномов:

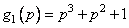
или (1.10)

.

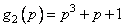Коды, генерируемые порождающими полиномам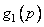и и , квивалентны. Кодовые слова кода (7,4), генерируемые полиномом 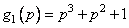даны в табл. 1.1

В общем полином можно факторизовать так:

,

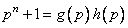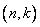где - означает порождающий полином для циклического кода, 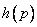означает проверочный полином степени 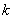. Последний можно использовать для генерирования дуального кода.

Таблица 1.1 Циклический код (7,4). Порождающий полином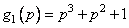

Информационные биты	Кодовые слова
							]

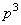
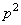
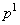
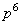
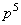
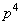
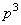
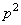
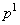
С этой целью можно использовать полином, обратный 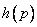, определяемый так:

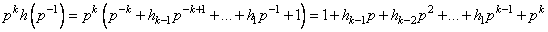(1.11)

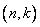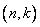Ясно, что делится без остатка и на обратный полином. Следовательно, является порождающим полиномом циклического кода. Этот циклический код дуален коду , генерируемому порождающим полиномом . Таким образом, дуальный код образует нуль-пространство циклического кода.

Пример 1.2 Рассмотрим циклический код, дуальный коду (7,4), генерированному в примере 1.1 Этот дуальный циклический код (7,3) связан с проверочным полиномом

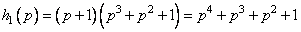. (1.12)

Обратный полином равен

.

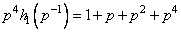Этот полином генерирует дуальный код (7,3), данный в таблице 1.1 Читатель может убедиться в том, что кодовые слова дуального кода (7,3) ортогональны кодовым словам циклического кода (7,4) из примера 1.1.

Желательно показать, как можно получить порождающую матрицу из порождающего полинома циклического кода 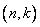. Как указано выше, порождающую матрицу для 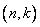кода можно сконструировать из любого набора 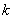линейно независимых кодовых слов. По заданному порождающему полиному легко генерировать набор 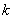линейно независимых кодовых слов – это кодовые слова, соответствующие набору 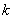линейно независимых полиномов .

Таблица 1.2 Дуальный код (7,3). Порождающий полином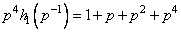

Информационные биты	Кодовые слова

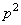
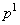
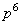
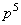
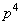
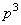
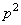
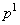
Поскольку любой из полиномов степени меньшей или равной 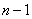, который делится на , можно выразить как линейную комбинацию этих полиномов, набор образует базис размерностью 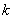. Следовательно, кодовые слова, связанные с этими полиномами, формируют базис размерности 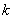для циклического кода .

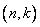Не нашли, что искали? Воспользуйтесь поиском: