Дебай-Хюккель теориясы

Электролит ерітінділер теориясының негізгі жайыттары 1923ж Дебай және Хюккельмен айтылған. Электролиттердің статистикалық теориясы келесі жағдайларға сәйкес келеді: иондар ерітінді көлемінде ретсіз таралмай, кулонның әсерлесу заңына сәйкес таралған. Жеке иондардың жан-жағында ион атмосферасы (ион бұлты) бар – ол тқарама – қарсы зарядталған ионнан тұратын сфера. Сфера құрамына кіретін иондар үздіксіз басқа иондармен орнын ауыстырып отырады. Ерітіндідегі барлық иондар бірдей (тең), олардың әрбіреуі иондық атмосферасымен қоршалған, сонымен қатар центрлік ион басқа ионның иондық атмосферасының құрамына кіреді.

χ = - ерітінді концентрациясына және Т -ға тәуелді шама, бірақ потенциалға тәуелді емес; ұзындыққа кері өлшем бірлігіне ие; бұл орталық ионның жан-жағындағы иондық атмосфераның орталық ионнан r арақашықтыққа алыстаған кездегі тығыздығының өзгерісін сипаттайды.

1/c шама сипаттамалық ұзындық деп атайды; оны иондық атмосфераның радиусымен теңдестіруге болады. Ол электролит ерітіндісінің теориясында үлкен мәнге ие.

Активтілік коэффициенті үшін келесі теңдеу алынған:

= - A |z₊×z_-| (1)

А коэффициенті Т және D -ға тәуелді, (DT)^3/2 -ге кері пропорционал

1-1 зарядты электролиттердің сулы ерітіндісі үшін 298К –де, ерітіндінің диэлектрлік өткізгіштігі және еріткіш (78,54) тең деп алып, келесідей жазуға болады:

= - A = - A = - 0,51

Сөйтіп, электролиттің сұйылтылған ерітінділері үшін эмпириялық табылған теңдеуі сияқты Дебай және Хюккель теориясы да активтілік коэффициенті үшін теңдеу алуға мүмкіндік береді. Яғни, теория тәжірибемен сапалық сәйкестікте жатыр. Осы теорияны өңдеген кезде келесі жорамалдар жасалды:

Электролиттегі иондар санын электролиттің аналитикалық концентарциясынан табуға болады, өйткені ол электролит толық диссоциаланған (a = 1) деп есептеді. Сондықтан, Дебай және Хюккель теориясын кейбір кездерде толық диссоциация теориясы деп те айтады. Бірақ оны a ¹ 1 кездерде де қолдануға болады.

Есептеу жүргізілгенде ерітінді мен таза еріткіштің дтэлектрлік өткізгіштігі тең деп алынады, бұл тек сұйылтылған ерітінділер үшін ғана жарамды (н/е дұрыс).

Айтылып кеткен жорамалдарға байланысты Дебай және Хюккель теориясы тек төмен валенттілікке ие иондары бар сұйылтылған электролит ерітінділерге қолданылады. (1) теңдеу осы шекті жағдайға сәйкес келеді және Дебай-Хюккельдің шекті заңы деп аталады немесе Дебай-Хюккельдің бірінші жақындау теориясын көрсетеді.

Дебай-Хюккельдің шекті заңы 1-1 зарядты электролиттің, әсіресе өте сұйылтылған ерітінділер үшін, активтілік коэффициенттердің дұрыс мәндерін береді. Теорияның тәжірибемен сәйкестігі электролит концентрациясы, ион заряды өскен сайын және еріткіштің диэлектрлік өткізгіштігі төмендеген сайын, яғни иондардың арасындағы әрекеттесу күші өсуімен, төмендейді.

Екінші жақындауда орташа активтілік коэффициенті келесі теңдеумен сипатталады:

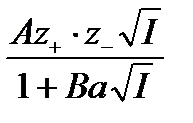= - (2)

мұнда А бұрынғы мәнін сақтайды; а ионның орташа эффективті диаметрі деп аталған, ұзындық өлшеміне ие, эмпириалық тұрақты; В = c/ , В Т -мен бірге біраз өзгереді. Сулы ерітінділер үшін В а 1 -ге жуық.

Теорияның екінші жақындауындағы негізгі жағдайларды сақтап Хюккель ерітінді концентрациясы өскен кезде диэлектрлік өткізгіштік тқмендейтінін ескерді. Оның төмендеуі еріткіштің дипольінің ионның жан-жағында бағытталуына байланысты, осының нәтижесінде сыртқы өрістің эффектісіне олардың рекциясы төмендейді. Хюккель теңдеуі келсі түрде беріледі:

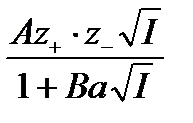= - + C I (3)

мұнда С –эмпириялық константа.

В және С мәндерін дұрыс таңдаған кезде Хюккель формуласы тәжірибемен жақсы сәйкес келеді және есептеу кезінде кең қолданылады. Иондық күш төмендеген кезде (3) теңдеу Дебай және Хюккельдің екінші жақындау теориясының формуласына айналды ((2) теңдеу), содан кейін Дебай-Хюккельдің шекті заңына ((1) теңдеу).

Дебай-Хюккель теориясы ары қарай дамыған кезде және қабылданған жорамалдарды ескермеген кезде оның тәжірибемен сәйкестігі жақсарады және оның қолданылу аймағы кеңейеді, алайда бұған теориялық теңдеудің жартылай эмпириялыққа айналған кезде ғана қол жеткізе аламыз.

Дебай және Хюккель ионның заряды мен потенциалының байланысы арқылы, Лаплас опператорын қолдана отырып, иондық атмосфераның қалыңдығын тапты:

Бұл теңдеуді былай өзгертейік:

Не нашли, что искали? Воспользуйтесь поиском: