
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Симметричные составляющие
Сущность метода симметричных составляющих состоит в разложении несимметричной системы векторов (токов или напряжений) на три симметричные системы: прямой, обратной и нулевой последовательностей. Симметричные составляющие какой-либо величины обозначаются соответственно индексами 1 - прямая, 2 – обратная, 0 – нулевая последовательность. Например, для несимметричной системы токов:
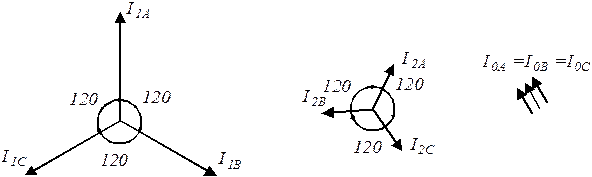
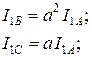
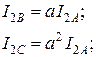
где 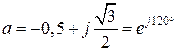 - оператор поворота на 120 градусов в положительном направлении.
- оператор поворота на 120 градусов в положительном направлении. 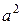 - поворот на 240 градусов в положительном направлении или на 120 градусов в отрицательном;
- поворот на 240 градусов в положительном направлении или на 120 градусов в отрицательном; 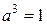 - поворот на 360 градусов (полный оборот).
- поворот на 360 градусов (полный оборот).
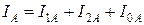 ,
,
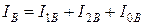 ,
,
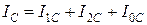
По умолчанию подразумевается, что все симметричные составляющие относятся к фазе А, т.е. фаза А является особой. Тогда фазные величины и их симметричные составляющие связаны следующими соотношениями:
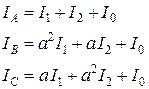
Или в матричной форме записи:
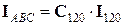 ,
,
где
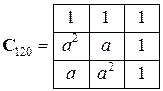 ,
,
для обратного преобразования следует обратить матрицу 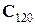 , тогда
, тогда
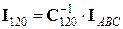 ,
,
где
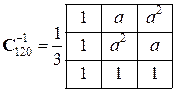
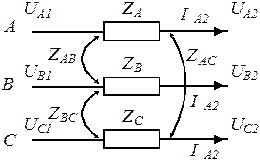 |
Рассмотрим, в качестве примера, запись уравнений, связывающих токи и падения напряжения на участке цепи.
Помимо собственных сопротивлений фаз 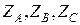 в общем случае имеются взаимные сопротивления между фазами, обусловленные взаимоиндукцией, поэтому схемы фаз оказываются связанными между собой.
в общем случае имеются взаимные сопротивления между фазами, обусловленные взаимоиндукцией, поэтому схемы фаз оказываются связанными между собой.
Для одного такого трехфазного элемента может быть составлена система уравнений:
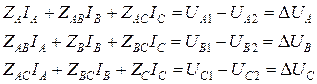
или в матричной форме
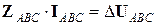 ,
,
Рассмотрим перевод данного выражения в систему симметричных составляющих:
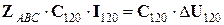 ,
,
Умножим левую и правую часть данного выражения на матрицу 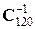
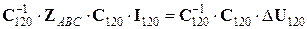 ,
,
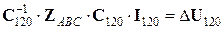 ,
,
Целесообразно ввести обозначение сопротивления участка цепи в симметричных составляющих:
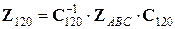
Тогда выражение связывающее токи и падения напряжений в симметричных составляющих запишется как:
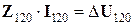
Рассмотрим частный случай, когда уравнения записываются для симметричного участка цепи, то есть для него справедливы равенства:
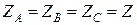 – собственные сопротивления всех трех фаз равны,
– собственные сопротивления всех трех фаз равны,
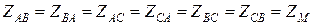 – взаимные сопротивления всех трех фаз равны,
– взаимные сопротивления всех трех фаз равны,
Для одного такого трехфазного элемента может быть составлена система уравнений:
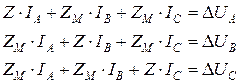
Тогда матрица сопротивлений трехфазной ветви в фазных координатах запишется следующим образом:
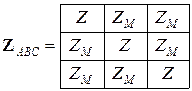 ,
,
Рассмотрим перевод данной системы уравнений в симметричные составляющие, для чего следует найти матрицу сопротивлений трехфазной ветви в симметричных составляющих
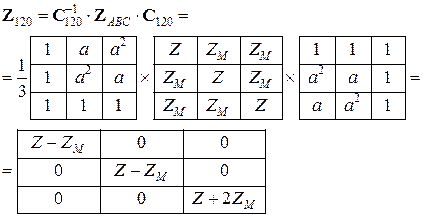
Таким образом, система уравнений
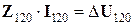 ,
,
запишется как
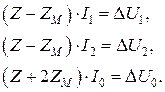
В полученных уравнениях переменные разделены, что существенно упрощает решение практических задач. То есть рассмотрение симметричных элементов ЭЭС удобнее выполнять в симметричных составляющих, а не в фазных координатах.
| <== предыдущая лекция | | | следующая лекция ==> |
| Анабиоз - резкое торможение метаболизма и всех форм активности при воздействии экстремальных условий существования. | | | ДЕРЖАВНЕ ЕКОНОМІЧНЕ РЕГУЛЮВАННЯ ПЕРВИННИХ СУБ'ЄКТІВ ГОСПОДАРЮВАННЯ. |
Не нашли, что искали? Воспользуйтесь поиском: