Основные сведения о матрицах

Матрицы широко используются для математического описания объектов и процессов. Excel в полной мере поддерживает операции и арифметические действия над матрицами.

- Математическая запись прямоугольной матрицы A размером m*n выглядит так:

- Матрица, состоящая из одной строки (столбца), называется вектором:

- Если m=n, то матрица называется квадратной n-го порядка.

Если в квадратной матрице элементы равны 0, а диагональные элементы равны 1, то матрица называется единичной и диагональной.

Единичная матрица 3-го порядка выглядит так:

Основные операции над матрицами и соответствующие функции Excel следующие:

- транспонирование матрицы – функция ТРАНСП из категории «Ссылки и массивы»;

- вычисление определителя матрицы – функция МОПРЕД из категории «Математические»;

- нахождение обратной матрицы – функция МОБР из категории «Математические»;

сложение, вычитание;

- умножение – функция МУМНОЖ из категории «Математические»;

1. Операция «Транспонирование»

В транспонированной матрице А^Т (или А^') столбцы исходной матрицы А заменяются строками, т.е. если A=(a_ij), то А^Т=(а_ji).

Транспонируем матрицу A1:D2 в матрицу A4:B7.

рис.1.

Из рис.1. видно, что функция ТРАНСП возвращает горизонтальный диапазон ячеек в виде вертикального и наоборот.

Проделайте следующее:

1) набрать исходный диапазон A1:D2;

2) выделить диапазон ячеек А4:B7 и вызовите мастер функций;

3) в окне мастера функций выбрать функцию ТРАНСП и указать диапазон исходного массива A1:D2;

4) завершить формулу массива.

2. Операция «Вычисление определителя»

Определитель - это числовая характеристика квадратной матрицы и вычисляется из значений ее элементов. Если =0, то матрица называется вырожденной.

Для матрицы 1-го порядка А=(а₁₁) определитель равен =а₁₁.

Для матрицы 2-го порядка определитель равен .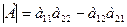

Определитель матрицы 3-го порядка содержит 6 слагаемых, 4-го порядка – 24 ит.д. – для матрицы n-го порядка число слагаемых равно n!.

Функция Excel МОПРЕД облегчает вычисления.

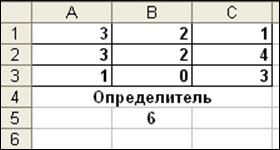
Вычислите определитель матрицы А1:С3, показанной на рисунке.

Проделайте следующее:

1) набрать исходный диапазон A1:С3;

2) выделить ячейку B5 и вызвать через мастер функций - функцию МОПРЕД;

3) в окне функции указать диапазон исходного массива A1:С3;

4) завершить формулу массива и получить значение определителя.

3. Операция «Нахождение обратной матрицы»

Обратные матрицы используются для решения систем уравнений с несколькими неизвестными.

Обратная матрица А^-1 существует только для невырожденной матрицы А.

Для матрицы 2-го порядка

обратная матрица вычисляется так:

Функция МОБР облегчает подобные вычисления.

На рисунке приведена матрица А1:С3, а в А5:С7 – обратная матрица.

Проделайте следующее:

1) набрать исходный диапазон A1:С3;

2) выделить диапазон ячеек для обратной матрицы А5:С7 и вызвать через мастер функций - функцию МОБР;

3) в окне функции указать диапазон исходного массива A1:С3;

4) завершить формулу массива.

4. Операция «Сложение и вычитание матриц, умножение матрицы на число»

Следует выполнить поэлементное сложение (вычитание) матриц.

Складывать (вычитать) можно матрицы одного размера.

Рассмотрим операцию поэлементного сложения двух массивов.

Пусть, например слагаемыми будут матрицы M и N, содержащиеся в диапазонах А1:C2 и E1:G2.

Проделайте следующее:

1) выбрать на рабочем листе диапазон, например A4:C6, в который будет помещён результат поэлементного сложения двух массивов (от данного диапазона требуется, чтобы он имел тот же размер, что и массивы – слагаемые)

2) введите формулу: = А1:C2+ E1:G2

3) завершить формулу массива.

Не нашли, что искали? Воспользуйтесь поиском: