Решение его можно найти в виде

= .

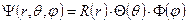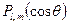
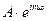Для 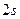- состояния атома водорода (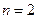, ) уравнение Шредингера имеет вид:

.

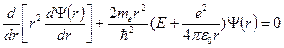Решение его:

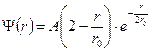, где

( - совпадает с радиусом первой боровской орбиты).

Это решение можно получить, подставив 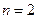и в общее решение радиального уравнения

= ,

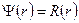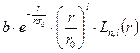где - полином Лагерра, имеющий () корней.

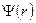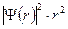Зависимости и для 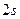- состояния приведены на рис.28 (а, б). Функция 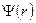имеет узел, т.е. совокупность точек в пространстве, где ее амплитуда обращается в нуль (рис.28а). Узлом волновой функции может быть точка, линия или поверхность. Узел 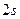- орбитали можно представить в виде сферической поверхности радиусом 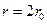, окружающей ядро. Максимум функции 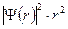приходится на 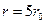(рис.28б).

Для 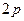- состояния (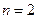, 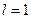) полином Лагерра не имеет корней (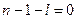), поэтому получаем

.

Максимум этой функции приходится на . Плотность вероятности в зависимости от модуля радиуса для 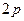- состояния

= .

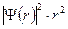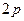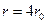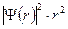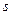Максимальная вероятность обнаружения электрона в - состоянии приходится на . Функции для -состояни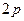й, -, - и 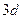- состояний приведены на рис.29.

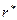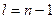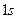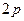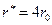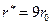Исследования распределения радиальной составляющей плотности вероятности обнаружения электрона в сферических слоях равной толщины в атоме водорода показывают, что с боровским радиусом совпадают , соответствующие состояниям с максимальным при данном , т.е. состояниям (), (), () и т.д.

Плотность вероятности локализации электрона в некоторой точке пространства равна

,

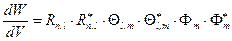но, поскольку 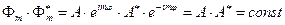, то плотность вероятности в этом случае не зависит от 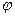, а зависит лишь от и 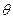. Т.к. 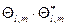(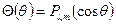) также не зависит от 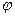, то график зависимости 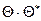обладает вращательной симметрией относительно оси (рис.30).

Для 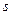- состояния существует только один энергетический уровень (, 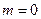). Соответствующий полином Лежандр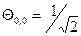а , а 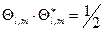, в этом случае

.

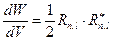В 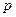- состояни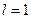и () при 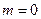полином Лежандра имеет вид 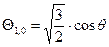, а и

.

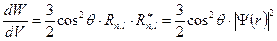Максимальная плотность вероятности – при 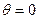, минимальная – при .

При

и

.

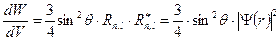Максимум этой функции приходится на , минимум - при .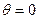

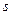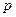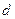Фигуры, изображенные на рис.31, показывают распределение полной плотности вероятности, определяемой угловой плотностью вероятности, которая, воздействуя на радиальную плотность вероятности, модулирует ее (для -, - и - состояний).

Не нашли, что искали? Воспользуйтесь поиском: