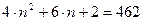ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Функции, проверяющие условия

Testing
Ниже приведена простая функция, которая проверяет некоторое условия для числа:
;; is-5?: number -> boolean;; определить, равно ли число n 5(define (is-5? n) (= n 5))Результатом функции будет true, тогда и только тогда, когда на вход подается число 5. Ее контракт содержит один новый элемент: слово «boolean» Точно так же как и число (number), boolean представляет класс значений, которые встроены в Схему. В отличие от number, boolean имеет только два значения: false и true.
Ниже приведена более интересная функция, результатом которой является булевское значение:
;; is-between-5-6?: number -> boolean;; определить находится ли число n между 5 и 6 (точно)(define (is-between-5-6? n) (and (< 5 n) (< n 6)))На вход функции подается число и результатом является true если число попадает в интервал между 5 и 6, но не является ни одним из этих чисел. Один из хороших путей понимания функции – это сказать, что она описывает интервал на числовой оси.

Границы интервала: Если граница интервала заключены в «(» или «)», это значит, что она исключается из интервала; если граница заключена в «[» или «]», то она включается в интервал.
Следующая третья функция представляет более сложную форму интервала:
;; is-between-5-6-or-over-10?: number -> boolean;; определить, попадает ли число n в интервал между 5 и 6 (точно);; или больше или равно 10(define (is-between-5-6-or-over-10? n) (or (is-between-5-6? n) (>= n 10)))
Функция возвращает true для двух диапазонов из числовой оси:

Левый диапазон это интервал между 5 и 6 не включая границ, правый диапазон – бесконечная линия начиная с 10. Любая точка из этих двух диапазонов удовлетворяет условию из функции is-between-5-6-or-over-10?
Все три функции проверяют числовые условия. Для проектирования или понимания подобных функций, мы должны понимать, что такое интервалы и их комбинации (известные как объединения). Следующие задания позволят закрепить знания об интервалах.
Упражнение 4.2.1 Переведите следующие пять интервалов числовой линии в функции Схемы, которые принимают на вход число и возвращают true, если число попадает в интервал и false в обратном случае.
1. полуинтервал (3,7]:

2. отрезок [3,7]:

3. полуинтервал [3,9):

4. объединение (1,3) и (9,11):

5. и диапазон чисел вне отрезка [1,3].
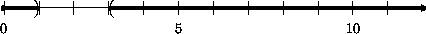
 Solution
Solution
Упражнение 4.2.2 Переведите следующие три функции в интервалы на числовой оси:
1. (define (in-interval-1? x) (and (< -3 x) (< x 0))) 2. (define (in-interval-2? x) (or (< x 1) (> x 2))) 3. (define (in-interval-3? x) (not (and (<= 1 x) (<= x 5))))Также сформулируйте контракты и постановки задач для этих трех функций.
Вычислите следующие выражения вручную:
- (in-interval-1? -2)
- (in-interval-2? -2)
- (in-interval-3? -2)
Покажите важные шаги. Используйте картинки для проверки результатов.  Solution
Solution
Упражнение 4.2.3 Математическое уравнение с одной переменной – это описание требований к неизвестному числу. Например, квадратное уравнение

это требование касающееся некоторого неизвестного числа x. Для x = -1 требование истинно.

Для x = 1 условия не выполняются

4 не равно 0. Число, для которого выполняются требования, называется решением уравнения.
Мы можем использовать Схему для формулирования уравнений, как функций. Если кто-то утверждает, что он знает решение, мы можем использовать функцию, для проверки является ли предложенное решение, настоящим решением. Ниже приведен пример такой функции
;; equation1: number -> boolean;; определить, является ли x решением уравнения x 2 + 2 · x + 1 = 0(define (equation1 x) (= (+ (* x x) (+ (* 2 x) 1)) 0))Когда мы применяем equation1 для какого-либо числа, мы получаем true или false:
(equation1 -1)= trueи
(equation1 +1)= falseЗапишите следующие уравнения в виде функций Схемы.
Являются ли числа 10, 12, 14 решениями этих уравнений.  Solution
Solution
Упражнение 4.2.4 Уравнения не только повсеместно используются в математике, они также постоянно используются в программировании. Мы использовали уравнения, чтобы показать, что функция может делать с примерами., мы использовали их для вычисления выражений вручную, и мы добавили их как тесты в окно Definitions.

Testing
Например, если нашей целью является определить функцию Fahrenheit -> Celsius, мы можем добавить наши примеры как тесты:
;; тестовое выражение:(Fahrenheit -> Celsius 32);; ожидаемый результат:0и
;; тестовое выражение:(Fahrenheit -> Celsius 212);; ожидаемый результат:100После нажатия на кнопку Execute, мы можем сравнить два числа. Если они равны, значит функция работает.
Поскольку, наши результаты становятся все более сложными, сравнивать значения будет все сложнее и сложнее. Используя =, мы можем вместо этого перевести все эти уравнения в условия, например:
(= (Fahrenheit -> Celsius 32) 0)и
(= (Fahrenheit -> Celsius 212) 100)Теперь, если результатом всех условий будет true, значит мы будем знать, что она работает для указанных примеров. Если какой-либо из результатов равен false, значит функция работает неправильно.
Переформулируйте тесты для упражнений 2.2.1, 2.2.2, 2.2.3 и 2.2.4, в виде условий.
Тестирование: Написание тестов – это хорошая практика, хотя нам необходимо больше знать про сравнения, чтобы создавать хорошие автоматические тесты. Для этого мы продолжаем обсуждение сравнений и тестирования в этом разделе.
Не нашли, что искали? Воспользуйтесь поиском: