Вычислять сумму вводимых с клавиатуры чисел, пока не встретится первое отрицательное число. Д/з №4

5. Вычислить без упрощения y = ;

6. Вычислить сумму ряда s=2,4,6.. 26

7. Вычислять квадратные корни вводимых положительных чисел, возводить в квадрат вводимые отрицательные числа, вычисления прекратить при вводе первого нуля.

8. Вычислить Y= 1 +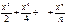

9. Вывести таблицу значений y=sin²(x) для x из промежутка [–2p;2p] с шагом p/4.

10. Вывести на экран в 3 столбика все числа, кратные 7
Циклы

1. Составьте программу, выводящую на экран квадраты чисел от 10 до 20.

2. Составьте программу, которая вычисляет сумму чисел от 1 до 100.

3. Составьте программу, которая вычисляет сумму чисел от 1 до N. Значение N вводится с клавиатуры.

4. Составьте программу, которая вычисляет произведение чисел от 1 до N. Значение N вводится с клавиатуры.

5. С клавиатуры вводятся N чисел. Составьте программу, которая определяет количество отрицательных, количество положительных и количество нулей среди введенных чисел.

6. Составьте программу, которая печатает таблицу перевода расстояний из дюймов в сантиметры (1 дюйм = 2,5 см) для значений длин от 1 до 20 дюймов.

7. Составить алгоритмы и программы перевода старинных русских мер длины и веса (счетчик цикла меняется от 1 до 10):

1. саженей в метры (1 сажень равна 2,1366 м)

2. футов в метры (1 фут равен 0,3048 м)

3. фунтов в килограммы (1 фунт равен 0,40951 кг)

8. В сберкассу на трехпроцентный вклад положили S рублей. Какой станет сумма вклада через N лет?

9. Ввести с клавиатуры 10 пар чисел. Сравнить числа в каждой паре и напечатать большие из них.

10. Даны натуральные числа от 20 до 50. Напечатать те из них, которые делятся на 3, но не делятся на 5.

11. Даны натуральные числа от 35 до 87. Найти и напечатать те, которые при делении на 7 дают остаток 1, 2 или 5.

12. Даны натуральные числа от 1 до 50. Найти сумму тех из них, которые делятся на 5 или на 7.

13. Ввести с клавиатуры 10 чисел. Если среди них есть числа, большие 15, заменить их на 15. Напечатать все полученные числа.

14. Ввести с клавиатуры 10 чисел – положительных и отрицательных. Заменить все отрицательные числа их модулями и напечатать все полученные 10 чисел.

15. Напечатать те из двузначных чисел, которые делятся на 4, но не делятся на 6.

16. Найти произведение двузначных нечетных чисел, кратных 13.

17. Найти сумму чисел от 100 до 200, кратных 17.

18. Ввести с клавиатуры 10 чисел. Если квадрат числа меньше 100, напечатать число и его квадрат.

19. Составьте программу, которая вычисляет сумму квадратов чисел от 1 до введенного вами целого числа n.

73. Написать программу, которая по заданным значениям чисел a и b находит a^b. В запросе укажите допустимые значения этих переменных

74. В бригаде, работающей на уборке сена, имеется N сенокосилок. Первая сенокосилка работала m часов, а каждая следующая на 10 минут больше, чем предыдущая. Сколько часов проработала вся бригада?

20. В ЭВМ вводятся координаты N точек. Опр., сколько из них попадает в круг радиусом R с центром в точке (a,b).

21. В ЭВМ вводятся по очереди данные о росте N учащихся класса. Определить средний рост учащихся класса.

22. Составить программу, сокращающую обыкновенные дроби.

23. Задано натуральное число N. Найти количество натуральных чисел, не превосходящих N и не делящихся ни на одно из чисел 2, 3, 5.

24. Два двузначных числа, записанных одно за другим, образуют четырехзначное число, которое делится на их произведение. Найти эти числа.

25. Даны два двузначных числа А и В. Из этих чисел составили два четырехзначных числа: первое число получили путем написания сначала числа A, а затем В; для получения второго сначала записали В, а потом А. Найти числа А и В, если известно, что первое четырехзначное число нацело делится на 99, а второе – на 49.

26. Дано натуральное n. Вычислить: 1/2² + 1/4² +... + 1/(2n) ⁿ .

27. Дано натуральное n. Вычислить: 1/1¹ + 1/2² +... + 1/n ⁿ.

28. Даны действительное a и натуральное n. Вычислить:

1. a!;

2. 1 + 1/2 + 1/3 +1/4 + … + 1/n;

3. 1 + 2 + 4 + 8 + … + 2¹⁰;

4. (1 + 2)*(1 + 2 + 3)*…*(1 + 2 + … +10);

5. 1/a² + 1/a⁴ + … 1/a²ⁿ;

6. sin x + sin x² + … sin xⁿ.

29. Составьте программу вычисления суммы всех двузначных чисел.

30. Дано натуральное n. Получить последовательность b₁, b₂,..., b_n, где при i =1,2,...,n значение b_i = i!

31. Дано натуральное n, действительные а₁,а₂,...,а_n. Получить: а₁а₂ + а₂ а₃,..., а_n-1а_n.

32. У первоклассника Пети m рублей. Мороженое стоит k рублей. Петя решил наесться досыта мороженого, для этого он покупал по одному мороженому и съедал ее до тех пор, пока ему хватало денег. Как Пете узнать, сколько денег останется у него в конце концов? Учтите, что Петя делить еще не умеет, а умеет только вычитать и складывать. Сколько мороженых он может съесть?

33. Бизнесмен взял ссуду m тысяч рублей в банке под 20% годовых. Через сколько лет его долг превысит s тысяч рублей, если за это время он не будет отдавать долг?

34. С помощью оператора while напишите программу вывода всех четных чисел в диапазоне от 2 до 100 включительно.

35. С помощью оператора while напишите программу определения суммы всех нечетных чисел в диапазоне от 1 до 99 включительно.

36. С помощью оператора while напишите программу определения идеального веса для взрослых людей по формуле: Ид. вес = рост – 100. Выход из цикла: значение роста = 250.

75. Имеется кусок ткани длиной М метров. От него последовательно отрезаются куски разной длины. Все данные по использованию ткани заносятся в компьютер. Компьютер должен выдать сообщение о том, что материала не хватает, если будет затребован кусок ткани, большей длины, чем имеется.

76. На соревнованиях по фигурному катанию оценки заносятся в компьютер. Составить программу для вывода на экран лучшего результата после каждого выступления фигуристов.

37. Первоначальное напряжение в цепи равно 200 вольт. Известно, что оно меняется через каждую секунду следующим образом: через одну секунду оно уменьшается на М%, а еще через секунду увеличивается на N%, затем снова уменьшается на М%, потом уменьшается на N% и т.д. Составить программу для определения, через сколько секунд напряжение в цепи превысит 220 вольт.

38. Напишите программу вычисления среднего геометрического модулей двух введенных с клавиатуры целых чисел. Программа должна использовать цикл while do. Условие выхода из цикла – значение числа, равное 999.

39. Напишите программу, которая определит первое отрицательное число последовательности: y = sin(i/100), i = 1,2,3…

40. Дано действительное число А, большее 1. Найти среди чисел 1, 1+1/2, 1+1/2+1/3,... первое, большее А и его номер.

41. Составить программу для вычисления числа е с точностью до 0.000001 по формуле 1 + 1/1! + 1/2! + 1/3! +...

42. С клавиатуры вводятся числа и последовательно суммируются. Найти количество введенных чисел, когда их сумма превысила 100.

43. Начав тренировки, спортсмен в первый день пробежал 10 км. Каждый день он увеличивал дневную норму на 10% нормы предыдущего дня.

· Какой суммарный путь пробежит спортсмен за 7 дней?

· В какой день впервые спортсмен пробежит более 20 км?

44. С помощью оператора repeat напишите программу, которая требует у вас пароль, например 111, и если пароль правильный, то печатает сообщение «Молодец!»

45. Составьте программу вычисления степени числа a с натуральным показателем n. (Записать варианты программы с разными видами циклов while, repeat, for).

46. Составьте программу, суммирующую штрафное время команд при игре в хоккей. Выводить на экран суммарное штрафное время обеих команд после любого его изменения. После окончания игры выдать итоговое сообщение.

47. Каждая бактерия делится на две в течение одной минуты. В начальный момент времени имеется одна бактерия. Составьте программу, которая подсчитывает количество бактерий на заданное вами целое значение момента времени.

48. Составьте программу получения в порядке убывания всех делителей данного числа.

49. Разложить число на простые множители.

50. Составьте программу определения наибольшего общего делителя двух натуральных чисел. (Реализовать в виде программы следующий вариант алгоритма Эвклида нахождения наибольшего общего делителя двух натуральных чисел: пока числа не станут равными, большее заменяется на разность большего и меньшего чисел. Когда числа станут равными одному и тому же числу d, то вычисления прекращаются: d равно наибольшему общему делителю исходных чисел).

51. Составьте программу определения наименьшего общего кратного двух натуральных чисел (использовать формулу: НОК*НОД=a*b)..

52. Составьте программу, определяющую максимальное из всех введенных вами чисел. (Пусть признаком конца ввода чисел является введенное число 0.)

53. Дано действительное число b>0. Последовательность a₁, a₂,… образована по следующему закону: a₁=1, a₂=2*a₁+1, …, a_i+1=2*a_i+1 (i=2,3,…). Требуется получить все a₁, a₂,…, меньшие или равные b.

54. Даны натуральное число n и действительное x. Вычислить: x ¹ /1! + x ² /2! +... + x ⁿ / n!

55. Найти наибольшее и наименьшее значение функции y = 3x² + x – 4, если на заданном интервале [a,b] x изменяется с шагом 0,1.

56. Найти с точностью 0.001 корни уравнений на указанных отрезках:

1. x² cos 2x + 1 = 0, [0, p/2];

2. x³ + x² + x +1 = 0, [-2, 1];

3. x⁵ - 0,3 | x-1| = 0, [0, 1];

4. 2x - cos x = 0, [0, p/2];

5. 0,9 x - sin Ö x - 0,1 = 0, [0, 1,5];

6. tg x - (x+1)/2 = 0, [0, p/4].

57. Пусть a₁ = 1; a_k = ka_k-1 + 1/k (k + 1,2, …). Дано натуральное n. Получить a_n.

58. Пусть a₁ = 1; a_k = a_k-1/k + k (k + 1,2, …). Дано натуральное n. Получить a_n.

59. На воду опущен шар радиуса r, изготовленный из вещества плотности r (r<1). Найти расстояние от центра шара до поверхности воды. Указание. При составлении программы воспользоваться формулой объема шарового сегмента высоты h: V = ph² (3r - h)/3, где r - радиус шара, h - высота шарового сегмента.

60. Составить программу, определяющую, является ли данное число N простым.

61. Составьте программу вывода на экран всех простых чисел, не превосходящих заданного N.

62. Найти все двузначные числа, сумма квадратов цифр которых делится на 13.

63. Составить программу вывода всех трехзначных чисел, сумма цифр которого равна данному натуральному числу.

64. Дано натуральное число n. Составить программу, подсчитывающую количество цифр числа n, сумму его цифр и определяющую его первую цифру.

65. В 1202 году итальянский математик Леонард Пизанский (Фибоначчи) предложил такую задачу: пара кроликов каждый месяц дает приплод – двух кроликов (самца и самку), от которых уже через два месяца уже получается новый приплод. Сколько кроликов будет через год, если в начале года имелась одна пара? Согласно условию задачи числа, соответствующие количеству кроликов, которые появляются через каждый месяц, составляют последовательность 1, 1, 2, 3, 5, 8, 13, 21, 34,… Составьте программу, позволяющие найти все числа Фибоначчи, меньше заданного числа N.

66. Найти первые сорок чисел Фибоначчи.

67. Найти первое число Фибоначчи, большее заданного числа М (М>1)

68. Вычислить сумму всех чисел Фибоначчи, которые не превосходят 1000.

69. Напишите программу, которая выведет на экран 10 строк по 5 случайных чисел в диапазоне 0…36.

Тема: "Циклические вычисления"

1 уровень (3 балла за задачу)

1. Напечатать таблицу перевода температуры из градусов по шкале Цельсия (С) с градусы шкалы Фаренгейта (F) для значений от 15 градусов С до 30 с шагом 1 градус. Перевод осуществлять по формуле F = 1,8C +32

2. Вычислить сумму первых 10 натуральных чисел.

3. Составить таблицу умножения для числа 12.

4. Дано 10 вещественных чисел. Найти величину наибольшего из них.

5. Вычислить значение функции: Y = SIN(1+SIN(2+SIN+...+SIN(39+SIN 40)...))

6. Считывается некоторое положительное число N (0 < N< 10). Определить все числа в диапазоне от 0 до 99, сумма которых равна N.

7. Ученик бежит по кругу. На старте стоит тренер и перед каждым новым кругом спрашивает ученика: "Пробежишь еще кружочек?". Подсчитать количество кругов.

8. Ученик бежит по кругу. На финише стоит тренер и после каждого нового круга спрашивает ученика: "Пробежишь еще кружочек?". Подсчитать количество кругов.

9. "Секундомер". Печатать значение параметра цикла в одном и том же месте чистого экрана (использовать задержку для изображения цифр).

10. Выводить на экран свое имя, пока не будет нажата какая-либо клавиша.

2 уровень (4 балла за задачу)

1. Вводятся числа. Определить сумму положительных и отрицательных чисел, общую сумму чисел и количество нулей.

2. Написать программу по переводу дробного числа из 10 системы счисления в N систему счисления (N <10).

3. Вывести по периметру экрана последовательно точки (для вывода на экран точки использовать "задержку" - DELAY(X)).

4. Ввести два натуральных числа А и В. Найти наибольший общий делитель двух чисел А и В.

5. Вычислить значение функции F(X,Y) = X + Y,
если X = 0.2, 0.5, 0.8, 1.1, а Y = 5, 4, 3, 2, 1 Результаты оформить в таблицу.

6. Ввести N. Подсчитать Y = n - n² + n³ - n⁴ + n⁵ - n⁶ + n⁷ - n⁸ + n⁹- n¹⁰

7. Вычислить приближенно площадь одной арки синусоиды, разделив отрезок от 0 до п на 10 частей и суммируя площади десяти прямоугольников с основанием п/10 и высотой, равной значению функции на правой границе каждого интервала.

8. Около стены наклонно стоит палка длиной Х. Один ее конец находится на расстоянии Y от стены. Определить значение угла L между палкой и полом для значений Х = 4,5 м и Y, изменяющегося от 2 до 3 м с шагом 0,2.

9. Начав тренировки, спортсмен в первый день пробежал 10 км. Каждый следующий день он увеличивал дневную норму на 10% от нормы предыдущего дня. Какой суммарный путь пробежит спортсмен за 7 дней.

10. Одноклеточная амеба каждые 3 часа делится на 2 клетки. Определить, сколько клеток будет через 3, 6, 9, 12,...24 часа. Попробовать изобразить это графически.

11. Написать программу угадывания (целых) чисел. Один из партнеров вводит в программу число, а второй должен отгадать это число. Причем на каждое предлагаемый вариант программа отвечает либо "больше", либо "меньше" до тех пор, пока число не будет отгадано.

12. Вычислить значение логической функции F = X Ù (X Ú Y) Ù (X Ú Z) для различных значений логических переменных X, Y, Z

13. В течение двух недель человек заключает пари на скачках. В первый день он делает ставку в 1 фунт и проигрывает. Во второй день, чтобы возместить свой проигрыш, он делает ставку в 2 фунта, но снова проигрывает. На третий день он ставит 3 фунта, однако опять проигрывает. Он упрямо продолжает увеличивать на 1 фунт свою ставку, но продолжает проигрывать. Сколько денег проиграет этот человек через 2 недели?

14. Припишите к 1022 слева и справа по одной цифре так, чтобы полученное число делилось на 7, 8 и 9.

15. В десятичной записи числа 42*4* две цифры пропущены. Восстановите их, если известно, что число кратно 72.

3 уровень (5 баллов за задачу)

1. Вводя в цикле по 5 оценок каждого учащегося, подсчитать число студентов, имеющих хотя бы одну оценку 2, и имеющих все оценки 5.

2. В цикле вводятся координаты точек. Определить, сколько из них принадлежит фигуре, ограниченной осью абсцисс и аркой синусоиды, построенной для аргумента от 0 до n.

^3. Окружность с центром в начале координат имеет заданный радиус R. Вводя последовательно координаты n точек, являющихся центрами других окружностей того же радиуса R, определить, сколько из этих окружностей пересекает заданную. Уравнение окружности: X² + Y² = R²

4. Составить программу помощника кассира в универсальном магазине. ПЭВМ должна запрашивать цену товара и его количество, подсчитывать суммарную стоимость купленных товаров, запрашивать сумму денег, внесенных покупателем, и определять причитающуюся ему сдачу.

5. Написать программу по переводу целого числа из системы счисления с основанием Р в систему счисления с основанием Q.

6. Написать программу по переводу дробного числа из системы счисления с основанием Р в систему счисления с основанием Q.

7. Составьте алгоритм игры в ЛОТО. Игра считается законченной, если фишками закрыты все числа на карточке.

8. "Секундомер". Печатать значение параметра цикла в одном и том же месте чистого экрана (использовать задержку для изображения цифр). Добавить к секундомеру индикацию минут и секунд. Например: 1 минута 10 секунд

10 минут 3 секунды

9. Найти все простые несократимые дроби, заключенные между 0 и 1, знаменатели которых не превышают 7 (дробь задается двумя натуральными числами – числителем и знаменателем.)

10. В 1202 году итальянский математик Леонард Пизанский (Фибоначчи) предложил такую задачу: пара кроликов каждый месяц дает приплод – двух кроликов (самца и самку), от которых через два месяца уже получается новый приплод. Сколько кроликов будет через год, если в начале года имелась одна пара? Согласно условию задачи числа, соответствующие количеству кроликов, которые появляются через месяц, составляют последовательность 1, 1, 2, 3, 5, 8, 13, 21, 34, … Составить программу, позволяющую найти все числа Фибоначчи, меньшие заданного N.

11. В старояпонском календаре был принят 60-летний цикл, состоявший из 12-летних подциклов. Подциклы обозначались названиями цвета: зеленый, красный, желтый, белый, черный. Внутри каждого подцикла годы носили названия животных: крысы, коровы, тигра, зайца, дракона, змеи, лошади, овцы, обезьяны, курицы, собаки и свиньи. 1984 год – год зеленой крысы – был годом начала очередного цикла. Напишите программу, которая вводит номер некоторого года и печатает его название по старояпонскому календарю.

12. Ввести координаты точки. Определить принадлежит ли она кольцу, образованному двумя окружностями с радиусами R и Р и с центрами в начале координат. Уравнение окружности:

13. Вы положили деньги в размере К рублей в сбербанк на срочный депозит сроком на M месяцев из расчета N% годовых. Вычислите причитающуюся вам через Р месяцев сумму.

14. Исследовать положительное вещественное число А, в котором определить значения целой части и дробной части, количество цифр в целой части числа.

15. Билет называется «счастливым», если в его номере сумма первых трех цифр равна сумме последних трех. Подсчитать число тех «счастливых» билетов, у которых сумма трех цифр равна 13.

16. Ввести значение времени (часов, минут, секунд) и определить угол (в градусах) между положением часовой стрелки в начале суток и в текущее время.
Например, если текущее время составляет 3 ч 30 мин 00 с, то этот угол составит 105°.

Не нашли, что искали? Воспользуйтесь поиском: