Вычисление определенного интеграла.

Пусть в интеграле нижний предел а = const, а верхний предел b изменяется. Очевидно, что если изменяется верхний предел, то изменяется и значение интеграла.

Обозначим = Ф(х). Найдем производную функции Ф(х) по переменному верхнему пределу х.

Аналогичную теорему можно доказать для случая переменного нижнего предела.

Теорема: Для всякой функции f(x), непрерывной на отрезке [a, b], существует на этом отрезке первообразная, а значит, существует неопределенный интеграл.

Теорема: (Теорема Ньютона – Лейбница)

Если функция F(x) – какая- либо первообразная от непрерывной функции f(x), то

это выражение известно под названием формулы Ньютона – Лейбница.

Доказательство: Пусть F(x) – первообразная функции f(x). Тогда в соответствии с приведенной выше теоремой, функция - первообразная функция от f(x). Но т.к. функция может иметь бесконечно много первообразных, которые будут отличаться друг от друга только на какое – то постоянное число С, то

при соответствующем выборе С это равенство справедливо для любого х, т.е. при х = а:

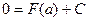
Тогда .

А при х = b:

Заменив переменную t на переменную х, получаем формулу Ньютона – Лейбница:

Теорема доказана.

Иногда применяют обозначение F(b) – F(a) = F(x) .

Формула Ньютона – Лейбница представляет собой общий подход к нахождению определенных интегралов.

Что касается приемов вычисления определенных интегралов, то они практически ничем не отличаются от всех тех приемов и методов, которые были рассмотрены выше при нахождении неопределенных интегралов.

Точно так же применяются методы подстановки (замены переменной), метод интегрирования по частям, те же приемы нахождения первообразных для тригонометрических, иррациональных и трансцендентных функций. Особенностью является только то, что при применении этих приемов надо распространять преобразование не только на подинтегральную функцию, но и на пределы интегрирования. Заменяя переменную интегрирования, не забыть изменить соответственно пределы интегрирования.

Замена переменных.

Пусть задан интеграл , где f(x) – непрерывная функция на отрезке [a, b].

Введем новую переменную в соответствии с формулой x = j(t).

Тогда если

1) j(a) = а, j(b) = b

2) j(t) и j¢(t) непрерывны на отрезке [a, b]

3) f(j(t)) определена на отрезке [a, b], то

Тогда

Пример.

При замене переменной в определенном интеграле следует помнить о том, что вводимая функция (в рассмотренном примере это функция sin) должна быть непрерывна на отрезке интегрирования. В противном случае формальное применение формулы приводит к абсурду.

Пример.

, с другой стороны, если применить тригонометрическую подстановку,

Т.е. два способа нахождения интеграла дают различные результаты. Это произошло из-за того, что не был учтен тот факт, что введенная переменная tgx имеет на отрезке интегрирования разрыв (в точке х = p/2). Поэтому в данном случае такая подстановка неприменима. При замене переменной в определенном интеграле следует внимательно следить за выполнением перечисленных выше условий.

Не нашли, что искали? Воспользуйтесь поиском: