Математика задачи операционное исчисление

Формулы Дюамеля. Применение их к решению дифференциальных уравнений

Иногда изображения приводятся к виду , причем оригиналы изображений и известны, т.е. и 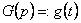. Тогда оригинал изображения 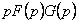можно найти через оригиналы и следующим образом.

Выражение 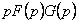можно записать в виде

или

.

По свойству дифференцирования оригинала имеем и Применяя теперь теорему Бореля к изображениям и , получаем

или

. (23)

Аналогично получается формула

. (24)

Соотношения (23) и (24) называются формулами Дюамеля, а интегралы в правых частях формул называются интегралами Дюамеля. Заметим, что можно использовать свойство симметрии свертки функций и , а также и , и получить еще две формулы Дюамеля:

. (25)

. (26)

Формулы Дюамеля применяются, например, для решения дифференциальных уравнений в некоторых ситуациях.

Пусть известно решение линейного дифференциального уравнения с постоянными коэффициентами с единичной правой частью и нулевыми начальными условиями в нуле:

, (27)

. (28)

Найти решение аналогичного дифференциального уравнения с правой частью :

(29)

при тех же начальных условиях (28).

Решение задачи. Предположим, что искомое решение , функция и решение уравнений (27) – (28) являются оригиналами, причем , , . Тогда для дифференциальных уравнений (27) – (28) и (29) – (28) операторные уравнения запишутся соответственно

и

.

Разделив равенства, получим или . Применяя к формулы Дюамеля (23) – (26), получим решение уравнения (29) при (28), например, в виде или и т.д.

ПРИМЕР 35. Найти решение дифференциального уравнения при .

Решение. Рассмотрим вспомогательное уравнение при . Ему соответствует решение , .

Для решения исходного уравнения воспользуемся формулой Дюамеля (24) при и , получаем

.

Итак, решение уравнения есть

.

Теорема Бореля и формулы Дюамеля дают дополнительные возможности нахождения оригинала по изображению.

Задание

Используя формулу Дюамеля, решить дифференциальное уравнение при .

Ответ: , .

Проверить, что – решение дифференциального уравнения при . Найти решение уравнения при .

Ответ: , .

Выяснить, является ли векторное поле гармоническим

Интегральное исчисление функции одной переменной.

При решении задач этой темы необходимо знать:

Определение и свойства неопределенного интеграла.

Таблицу основных интегралов.

Основные методы интегрирования.

Стандартные методы интегрирования наиболее часто встречающихся классов функций.

Определение, свойства и способы вычисления определенного интеграла.

Не нашли, что искали? Воспользуйтесь поиском: