Составление аналитического выражения функции и построение логической схемы по табличному заданию функции.

Синтез комбинационных устройств может быть произведен по табличному заданию функции по «0» и «1». Рассмотрим для примера синтез по «1». Для всех значений аргументов х₁, х₂, х₃, где функция задана как «1» берется их конъюнкция, если аргумент равен «1», если же 0 – конъюнкция их инверсий. От полученных конъюнкций берется дизъюнкция.

Например, функция от трех аргументов задана следующей таблицей:

Это значит, что при любых наборах аргументов ч кроме второго и последнего, аргумент у будет равен 0. Составляем для второго набора выражение: .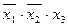

Для последнего набора: х₁ х₂ х₃

Составим аналитическое выражение функции:

Схема должна содержать инверсию сигналов х₁, х₂, две схемы «И» и одну двухвходовую схему «ИЛИ»

Ход работы:

1. Изучить теоретическое обоснование;

2. Выполнить задание в тетради.

3.

Задания:

Задание № 1

Записать логическую функцию, описывающую состояние логической схемы. Составить таблицу истинности.

а)

б)

Задание № 2

Записать логическую функцию, описывающую состояние логической схемы. Составить таблицу истинности.

Задание №3

Построить логические схемы по формулам и составить таблицу истинности

а) F= (AvB)&(Cv`B)

б) F= (A&B&C)

Задание №4

Построить логические схемы по формулам и составить таблицу истинности

а)F= (XvY) & (Yv`X).

б)F= ((XvY) & (`ZvX)) & (ZvY).

Не нашли, что искали? Воспользуйтесь поиском: