ЧАСТНЫЕ ПРОИЗВОДНЫЕ, ЧАСТНЫЕ ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ

ПРАКТИЧЕСКАЯ РАБОТА № 4.

Тема: «Функция нескольких переменных.

Нахождение частных производных».

Теоретические сведения.

ОПРЕДЕЛЕНИЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ.

Рассмотрим два множества. Пусть множество D есть подмножество множества R² ={(x,y) } на плоскости, т.е. DÌR², а множество Z есть подмножество множества R на прямой, т.е. ZÌR. Соотношение между множеством D и множеством Z, при котором каждому элементу (x,y) множества D соответствует один и только один элемент z множества Z, называется функцией двух переменных.

Множество D называется областью определения функции и обозначается D(z). Для функции двух переменных вводится обозначение z = f (x;y), (x;y) Î D (z).

ЧАСТНЫЕ ПРОИЗВОДНЫЕ, ЧАСТНЫЕ ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ

Пусть функция z=f (x; y) определена в открытой области D и точка (x₀; y₀)Î D. Дадим значению x₀ приращение D x, сохраняя значение второго аргумента неизменным и равным y₀. Тогда функция f получит приращение 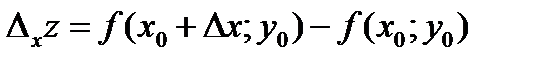, которое, естественно, назвать ее частным приращением по переменной x или частным приращением в направлении оси ОX.

Частной производной первого порядка функции f по переменной x в точке (x₀; y₀) называется предел отношения частного приращения D _xz функции f в точке (x₀; y₀) к приращению D x, когда D x ®0.

Частная производственная функции z=f (x; y) в точке (x₀; y₀) по переменной x обозначается чаще всего следующим образом:

Итак, .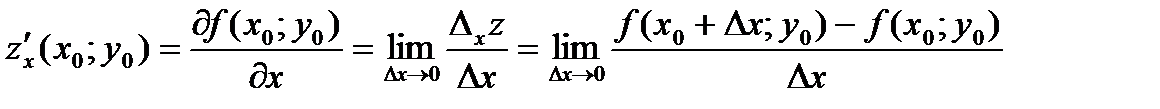

Аналогично следует поступать при вычислении частной производной функции z=f (x;y) по y. Только теперь при нахождении 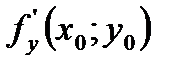надо брать производную от f (x;y) по y, считая x постоянным.

Чтобы вычислить частную производную от функции z=f (x;y) по одному из ее аргументов, нужно вычислить производную от функции f по этому аргументу, считая другой аргумент постоянным.

Пусть в области D функция z=f (x;y) имеет частные производные 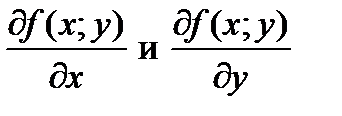. Естественно поставить вопрос об определении частных производных по x и y от этих функций в точке (x₀; y₀)ÎD. Так мы придем к понятию частных производных второго порядка от функции z=f(x; y) в точке (x₀,y₀). Таким образом, каждая из производных функций 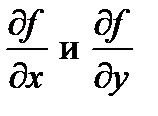порождает две производные второго порядка, которые обозначаются следующим образом:

Возможны и другие обозначения частных производных второго порядка. Например,

.

Частные производные, взятые по различным переменным, называются смешанными.

Не нашли, что искали? Воспользуйтесь поиском: