
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Элементы линейной алгебры и аналитической геометрии
11-20. В пирамиде SABC: треугольник АВС – основание пирамиды, точка S – ее вершина. Даны координаты точек A, B, C, S. Сделать чертеж. Найти:
1) длину ребра АВ;
2) угол между ребрами АВ и AS;
3) угол наклона ребра AS к основанию пирамиды;
4) площадь основания пирамиды;
5) объем пирамиды;
6) уравнение прямой АВ;
7) уравнение плоскости АВС;
8) проекцию вершины S на плоскость АВС;
9) длину высоты пирамиды.
11. А(-2;0;0); В(0;3;0); C(0;0;1); S(0;2;3).
12. А(4;0;0); В(0;-8;0); C(0;0;2); S(4;6;3).
13. А(-2;0;0); В(0;6;0); C(0;0;2); S(-1;6;4).
14. А(1;0;0); В(0;2;0); C(0;0;2); S(1;1;4).
15. А(-3;0;0); В(0;-2;0); C(0;0;1); S(-2;-1;3).
16. А(6;0;0); В(0;-3;0); C(0;0;2); S(4;-3;4).
17. А(3;0;0); В(0;-6;0); C(0;0;1); S(1;-3;3).
18. А(-4;0;0); В(0;4;0); C(0;0;2); S(-2;4;3).
19. А(-6;0;0); В(0;2;0); C(0;0;3); S(-3;2;5).
20. А(-1;0;0); В(0;5;0); C(0;0;2); S(-1;3;4).
51-60. Дана система линейных уравнений: 
Доказать ее совместность и решить тремя способами: 1) методом Гаусса; 2) средствами матричного исчисления; 3) по правилу Крамера.
51.  52.
52. 
53.  54.
54. 
55.  56.
56. 
57.  58.
58. 
59.  60.
60. 
71-80. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей А.
71.  72.
72. 
73. 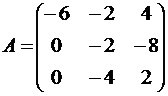 74.
74. 
75.  76.
76. 
77.  78.
78. 
79. 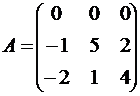 80.
80. 
91-100. Дано комплексное число a. Требуется: 1) записать число a в алгебраической и тригонометрической формах; 2) найти все корни уравнения z3+a=0.
91.  . 92.
. 92.  . 93.
. 93.  .
.
94. 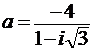 .95.
.95.  . 96.
. 96.  .
.
97.  . 98.
. 98.  . 99.
. 99.  . 100.
. 100.  .
.
111-120. Найти пределы функций, не пользуясь правилом Лопиталя.
111. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
112. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
113. а)  ; б)
; б) 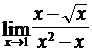 ;
;
в) 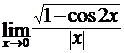 ; г)
; г)  .
.
114. а) 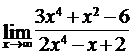 ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
115. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
116. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
117. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
118. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
119. а)  ; б)
; б) 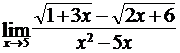 ;
;
в)  ; г)
; г)  .
.
120. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
Не нашли, что искали? Воспользуйтесь поиском: