
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Основные формулы и законы. где S- площадь поперечного сечения проводника.
 Сила тока
Сила тока

 ( если
( если  ).
).
 Плотность тока
Плотность тока
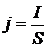 ,
,
где S - площадь поперечного сечения проводника.
 Плотность тока в проводнике
Плотность тока в проводнике
 ,
,
где  -скорость упорядоченного движения зарядов в проводнике, n - концентрация зарядов, e - элементарный заряд.
-скорость упорядоченного движения зарядов в проводнике, n - концентрация зарядов, e - элементарный заряд.
 Зависимость сопротивления от параметров проводника
Зависимость сопротивления от параметров проводника
 ,
,
где l - длина проводника, S - площадь поперечного сечения проводника,  - удельное сопротивление,
- удельное сопротивление,  - удельная проводимость.
- удельная проводимость.
 Зависимость удельного сопротивления от температуры
Зависимость удельного сопротивления от температуры
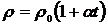 ,
,
где 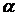 - температурный коэффициент сопротивления,
- температурный коэффициент сопротивления,  - удельное сопротивление при
- удельное сопротивление при  .
.
 Сопротивление при последовательном (а) и параллельном (б) соединении проводников
Сопротивление при последовательном (а) и параллельном (б) соединении проводников
а)  , б)
, б)  ,
,
где  - сопротивление
- сопротивление  го проводника, n – число проводников.
го проводника, n – число проводников.
 Закон Ома:
Закон Ома:
для однородного участка цепи
 ,
,
для неоднородного участка цепи
 ,
,
для замкнутой цепи
 ,
,
где U - напряжение на однородном участке цепи,  - разность потенциалов на концах участка цепи,
- разность потенциалов на концах участка цепи,  - ЭДС источника, r - внутреннее сопротивление источника тока.
- ЭДС источника, r - внутреннее сопротивление источника тока.
 Сила тока короткого замыкания
Сила тока короткого замыкания
 .
.
 Работа тока за время t
Работа тока за время t
.
 Мощность тока
Мощность тока
.
 Закон Джоуля-Ленца (количество теплоты, выделяемой при прохождении тока через проводник)
Закон Джоуля-Ленца (количество теплоты, выделяемой при прохождении тока через проводник)
.
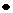 Мощность источника тока
Мощность источника тока

 Коэффициент полезного действия источника тока
Коэффициент полезного действия источника тока
 .
.
 Правила Кирхгофа
Правила Кирхгофа
1)  - для узлов;
- для узлов;
2)  - для контуров,
- для контуров,
где  - алгебраическая сумма сил токов, сходящихся в узле,
- алгебраическая сумма сил токов, сходящихся в узле,  - алгебраическая сумма ЭДС в контуре.
- алгебраическая сумма ЭДС в контуре.
2.1. На концах медного провода длиной 5 м поддерживается напряжение 1 В. Определить плотность тока в проводе (удельное сопротивление меди 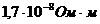 ).
).
А.  B.
B. 
С.  D.
D. 
2.2. Резистор сопротивлением 5 Ом, вольтметр и источник тока соединены параллельно. Вольтметр показывает напряжение 10 В. Если заменить резистор другим с сопротивлением 12 Ом, то вольтметр покажет напряжение 12 В. Определить ЭДС и внутреннее сопротивление источника тока. Током через вольтметр пренебречь.
A. [14 В; 2 Ом] B. [1,4 В; 2 Ом]
С. [14 В, 20 Ом] D. [140 В; 20 Ом]
2.3.  Определить силу тока в цепи, состоящей из двух элементов с ЭДС, равными 1,6 В и 1,2 В и внутренними сопротивлениями 0,6 Ом и 0,4 Ом соответственно, соединённых одноимёнными полюсами.
Определить силу тока в цепи, состоящей из двух элементов с ЭДС, равными 1,6 В и 1,2 В и внутренними сопротивлениями 0,6 Ом и 0,4 Ом соответственно, соединённых одноимёнными полюсами.
А. [0,4 A] B. [4 А] C. [40 мА] D. [40 А]
2.4. Гальванический элемент даёт на внешнее сопротивление 0,5 Ом силу тока 0,2 А. Если внешнее сопротивление заменить на 0,8 Ом, то ток в цепи 0,15 А. Определить силу тока короткого замыкания.
А. [0,45A] B.[45 мА] С.[4,5 А] D.[4,5 мА]
2.5. К источнику тока с ЭДС 12 В присоединена нагрузка. Напряжение на клеммах источника 8 В. Определить КПД источника тока.
А. [68%] B. [6,8%] С.[86%] D. [0,68%]
2.6. Внешняя цепь источника тока потребляет мощность 0,75 Вт. Определить силу тока в цепи, если ЭДС источника 2В и внутреннее сопротивление 1 Ом.
А. [0,5 и 1,5 А] В. [5 и 1,5 А] С. [0,5 A] D. [1,5 A]
2.7. Источник тока с ЭДС 12 В и внутренним сопротивлением 1 Ом подключён к нагрузке сопротивлением 9 Ом. Найти: 1) силу тока в цепи, 2) мощность, выделяемую во внешней части цепи, 3) мощность, теряемую в источнике тока, 4) полную мощность источника тока, 5) КПД источника тока. [1)1,2 A; 2)12,96 Вт; 3)1,44 Вт; 4)14,4 Вт; 5)90%]
2.8. Обмотка электрического кипятильника имеет две секции. Если включена одна секция, вода закипает через 10 мин, если другая, то через 20 мин. Через сколько минут закипит вода, если обе секции включить: а) последовательно; б) параллельно? Напряжение на зажимах кипятильника и КПД установки считать во всех случаях одинаковыми.
А. [а) 30 мин, б) 6,67 мин] В. [а) 6,67 мин; б) 30 мин]
С. [а) 10 мин; б) 20 мин] D. [а) 20 мин; б) 10 мин]
2.9. Амперметр сопротивлением 0,18 Ом предназначен для измерения силы тока до 10 А. Какое сопротивление надо взять и как его включить, чтобы этим амперметром можно было измерять силу тока до 100 А?
А. [0,02 Ом, параллельно] В. [0,02 Ом, последовательно]
С. [20 Ом, параллельно] D. [20 Ом, последовательно]
2.10. Вольтметр сопротивлением 2000 Ом предназначен для измерения напряжения до 30 В. Какое сопротивление надо взять и как его включить, чтобы этим вольтметром можно было измерять напряжение до 75 В?
А. [3000 Ом, последовательно] В. [3000 Ом, параллельно]
С. [0,03 Ом, последовательно] D. [0,03 Ом, параллельно]
2.11. * Ток в проводнике сопротивлением 100 Ом равномерно нарастает от 0 до 10 А в течение 30 с. Чему равно количество теплоты, выделившееся за это время в проводнике?
А. [100 кДж ] В. [100 Дж] С. [10 кДж ] D. [1000 Дж]
2.12.* Ток в проводнике сопротивлением 12 Ом равномерно убывает от 5 А до 0 в течение 10 с. Какое количество теплоты выделяется в проводнике за это время?
А. [1 кДж] В. [10 кДж] С. [100 Дж] D. [100 кДж]
2.13.* По проводнику сопротивлением 3 Ом течёт равномерно возрастающий ток. Количество теплоты, выделившееся в проводнике за 8 с, равно 200 Дж. Определить заряд, протекший за это время по проводнику. В начальный момент времени ток был равен нулю.
А. [20 Кл] В. [200 Кл] С. [40 Кл] D. [400 Кл]

 2.14.* Ток в проводнике сопротивлением 15 Ом равномерно возрастает от 0 до некоторого максимума в течение 5 с. За это время в проводнике выделилось количество теплоты 10 кДж. Найти среднее значение силы тока в проводнике за этот промежуток времени.
2.14.* Ток в проводнике сопротивлением 15 Ом равномерно возрастает от 0 до некоторого максимума в течение 5 с. За это время в проводнике выделилось количество теплоты 10 кДж. Найти среднее значение силы тока в проводнике за этот промежуток времени.
А. [10 А] В. [100 А] С. [1 кА] D. [10 кА]
2.15.* Ток в проводнике равномерно увеличивается от 0 до некоторого максимального значения в течение 10 с. За это время в проводнике выделилось количество теплоты 1 кДж. Определить скорость нарастания тока в проводнике, если сопротивление его 3 Ом.
А. [1А/с] В. [10 А/с] С. [1 кА/с] D. [10 кА/с]
2.16. На рис. 2.1 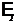 =
= 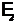 =
=  , R1 = 48 Ом, R2 = 24 Ом, падение напряжения U2 на сопротивлении R2 равно 12 В. Пренебрегая внутренним сопротивлением элементов, определить силу тока во всех участках цепи и сопротивление R3. [I1=0,25 A; I2=0,5 A; I3=0,75 A; R3=16 Ом]
, R1 = 48 Ом, R2 = 24 Ом, падение напряжения U2 на сопротивлении R2 равно 12 В. Пренебрегая внутренним сопротивлением элементов, определить силу тока во всех участках цепи и сопротивление R3. [I1=0,25 A; I2=0,5 A; I3=0,75 A; R3=16 Ом]
 |
|
Рис. 2.1 Рис. 2.2 Рис. 2.3
2.17. На рис. 2.2  =2В, R1= 60 Ом, R2= 40 Ом, R3=R4= 20 Ом, RG= 100 Ом. Определить силу тока IG через гальванометр. [1,49 мА]
=2В, R1= 60 Ом, R2= 40 Ом, R3=R4= 20 Ом, RG= 100 Ом. Определить силу тока IG через гальванометр. [1,49 мА]
2.18. Найти силу тока в отдельных ветвях мостика Уитстона (рис. 2.2) при условии, что сила тока, идущего через гальванометр, равна нулю. ЭДС источника 2В, R1= 30 Ом, R2= 45 Ом, R3= 200 Ом. Внутренним сопротивлением источника пренебречь. [I1=I2=26,7 мА, I3=I4= 4 мА]
2.19. На рис. 2.3 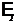 =10 В,
=10 В, 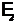 = 20 В,
= 20 В,  = 40 В, а сопротивления R1=R2=R3= 10 Ом. Определить силу токов через сопротивления (I) и через источники (
= 40 В, а сопротивления R1=R2=R3= 10 Ом. Определить силу токов через сопротивления (I) и через источники ( ). Внутренним сопротивлением источников пренебречь. [ I 1=1A, I 2=3A, I 3=2A,
). Внутренним сопротивлением источников пренебречь. [ I 1=1A, I 2=3A, I 3=2A,  =2A,
=2A,  =0,
=0,  =3A]
=3A]
2.20. На рис. 2.4 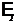 = 2,1 В,
= 2,1 В, 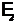 = 1,9 В, R1=45 Ом, R2= 10 Ом, R3= 10 Ом. Найти силу тока во всех участках цепи. Внутренним сопротивлением элементов пренебречь. [I1=0,04 A, I2=0,01 A, I3=0]
= 1,9 В, R1=45 Ом, R2= 10 Ом, R3= 10 Ом. Найти силу тока во всех участках цепи. Внутренним сопротивлением элементов пренебречь. [I1=0,04 A, I2=0,01 A, I3=0]

Рис. 2.4 Рис. 2.5 Рис. 2.6
2.21. На рис. 2.5 сопротивления вольтметров равны R1=3000 Ом и R2=2000 Ом; R3=3000 Ом, R4=2000 Ом;  =200 В. Найти показания вольтметров в случаях: а) ключ К разомкнут, б) ключ К замкнут. Внутренним сопротивлением источника пренебречь. [а)U1=120 В, U2=80 В, б)U1=U2=100 В]
=200 В. Найти показания вольтметров в случаях: а) ключ К разомкнут, б) ключ К замкнут. Внутренним сопротивлением источника пренебречь. [а)U1=120 В, U2=80 В, б)U1=U2=100 В]
2.22. На рис. 2.6 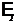 =
= 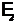 =1,5 В, внутренние сопротивления источников r1=r2=0,5 Ом, R1=R2= 2 Ом, R3= 1 Ом. Сопротивление миллиамперметра 3 Ом. Найти показание миллиамперметра. [75 мА]
=1,5 В, внутренние сопротивления источников r1=r2=0,5 Ом, R1=R2= 2 Ом, R3= 1 Ом. Сопротивление миллиамперметра 3 Ом. Найти показание миллиамперметра. [75 мА]
 2.23. На рис. 2.7
2.23. На рис. 2.7 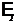 =
= 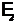 = 110 В, R1=R2= 200 Ом, сопротивление вольтметра 1000 В. Найти показание вольтметра. Внутренним сопротивлением источников пренебречь. [100 В]
= 110 В, R1=R2= 200 Ом, сопротивление вольтметра 1000 В. Найти показание вольтметра. Внутренним сопротивлением источников пренебречь. [100 В]
Рис. 2.7 Рис. 2.8 Рис. 2.9
2.24. На рис. 2.8 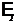 =
= 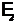 = 2В, внутренние сопротивления источников равны 0,5 Ом, R1= 0,5 Ом, R2= 1,5 Ом. Найти силу тока во всех участках цепи. [2,22 А, 0,44 А, 1,78 А]
= 2В, внутренние сопротивления источников равны 0,5 Ом, R1= 0,5 Ом, R2= 1,5 Ом. Найти силу тока во всех участках цепи. [2,22 А, 0,44 А, 1,78 А]
2.25. На рис. 2.9 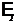 =
= 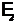 = 100 В, R1= 20 Ом, R2= 10 Ом, R3= 40 Ом, R4= 30 Ом. Найти показание амперметра. Внутренним сопротивлением источников и амперметра пренебречь. [1 А]
= 100 В, R1= 20 Ом, R2= 10 Ом, R3= 40 Ом, R4= 30 Ом. Найти показание амперметра. Внутренним сопротивлением источников и амперметра пренебречь. [1 А]
2.26. Какую силу тока показывает амперметр на рис. 2.10, сопротивление которого RA=500 Ом, если 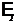 = 1 В,
= 1 В, 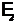 = 2 В, R3=1500 Ом и падение напряжения на сопротивлении R2 равно 1 В. Внутренним сопротивлением источников пренебречь.[1 мА]
= 2 В, R3=1500 Ом и падение напряжения на сопротивлении R2 равно 1 В. Внутренним сопротивлением источников пренебречь.[1 мА]
2.27. На рис. 2.11 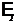 =1.5 В,
=1.5 В, 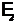 =1,6 В, R1=1 кОм, R2=2 кОм. Определить показания вольтметра, если его сопротивление RV=2 кОм. Сопротивлением источников пренебречь. [0,35 В]
=1,6 В, R1=1 кОм, R2=2 кОм. Определить показания вольтметра, если его сопротивление RV=2 кОм. Сопротивлением источников пренебречь. [0,35 В]
 | |||||||||
| |||||||||
| |||||||||
| |||||||||
 |
Рис. 2.10 Рис. 2.11 Рис. 2.12
2.28. На рис. 2.12 сопротивления R1= 5Ом, R2= 6 Ом, R3= 3 Ом. Найти показание амперметра, если вольтметр показывает 2,1 В. Сопротивлением источника и амперметра пренебречь.[0,2 А]
2.29. Определить ЭДС источника в схеме на рис. 2.13, если сила тока, текущего через него, равна 0,9 А, внутреннее сопротивление источника 0,4 Ом. R1=30 Ом, R2=24 Ом, R3 =50 Ом, R4 =40 Ом, R5 =60 Ом.
2.30. Найти показания амперметра в схеме на рис. 2.14, если ЭДС равна 19,8 В, внутреннее сопротивление 0,4 Ом, R1=30 Ом, R2=24 Ом, R3=50 Ом, R4=40 Ом, R5=60 Ом.
 |
Рис. 2.13 Рис. 2.14 Рис. 2.15
2.31. Найти величины всех сопротивлений в схеме на рис. 2.15, если через сопротивление R1 течёт ток 0,4 мкА, через сопротивление R2 ток 0,7 мкА, через сопротивление R3 – 1,1 мкА, через сопротивление R4 ток не течёт. Внутренним сопротивлением элементов пренебречь. E1=1,5 В; E2=1,8 В.

Рис. 2.16 Рис. 2.17 Рис. 2.18
2.32. Определить E1 и E2 в схеме на рис. 2.16, если R1=R4=2 Ом, R2=R3= 4 Ом. Ток, текущий через сопротивление R3 равен 1А, а через сопротивление R2 ток не течёт. Внутренние сопротивления элементов r1=r2=0,5 Ом.
2.33. Определить силу тока во всех участках цепи в схеме на рис. 2.17, если E1=11 В, E2=4 В, E3=6 В, R1=5 Ом, R2=10 Ом, R3=2 Ом. Внутренние сопротивления источников r1=r2=r3=0,5 Ом.
2.34. В схеме на рис. 2.18 R1=1 Ом, R2=2 Ом, R3=3 Ом, сила тока через источник равна 2А, разность потенциалов между точками 1 и 2 равна 2 В. Найти сопротивление R4.
Электомагнетизм
Основные формулы
• Магнитная индукция  связана с напряженностью
связана с напряженностью  магнитного поля соотношением
магнитного поля соотношением 
 ,
,
где  - магнитная постоянная,
- магнитная постоянная,
 - магнитная проницаемость изотропной среды.
- магнитная проницаемость изотропной среды.
• Принцип суперпозиции магнитных полей

 ,
,
где  - магнитная индукция, создаваемая каждым током или движущимся зарядом в отдельности.
- магнитная индукция, создаваемая каждым током или движущимся зарядом в отдельности.
• Магнитная индукция поля, создаваемая бесконечно длинным прямолинейным проводником с током,
 ,
,
где  - расстояние от проводника с током до точки, в которой определяется магнитная индукция.
- расстояние от проводника с током до точки, в которой определяется магнитная индукция.
• Магнитная индукция поля, создаваемого прямолинейным проводником с током конечной длины

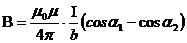 ,
,
где  - углы между элементом тока и радиус-вектором, проведенным из рассматриваемой точки к концам проводника.
- углы между элементом тока и радиус-вектором, проведенным из рассматриваемой точки к концам проводника.
• Магнитная индукция поля в центре кругового проводника с током
 ,
,
где  - радиус кругового витка.
- радиус кругового витка.
• Магнитная индукция поля на оси кругового проводника с током
 ,
,
где  - радиус кругового витка,
- радиус кругового витка,  - расстояние от центра витка до точки, в которой определяется магнитная индукция.
- расстояние от центра витка до точки, в которой определяется магнитная индукция.
• Магнитная индукция поля внутри тороида и бесконечно длинного соленоида
 ,
,
где  - число витков на единицу длины соленоида (тороида).
- число витков на единицу длины соленоида (тороида).
• Магнитная индукция поля на оси соленоида конечной длины
 ,
, 
где  - углы между осью катушки и радиус-вектором, проведенным из данной точки к концам катушки.
- углы между осью катушки и радиус-вектором, проведенным из данной точки к концам катушки.
• Сила Ампера, действующая на элемент  проводника с током
проводника с током  в магнитном поле,
в магнитном поле,
 ,
, 
где  - угол между направлениями тока и магнитной индукции поля.
- угол между направлениями тока и магнитной индукции поля.
• Магнитный момент контура с током


где 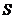 - площадь контура,
- площадь контура,
 - единичный вектор нормали (положительный) к плоскости контура.
- единичный вектор нормали (положительный) к плоскости контура.
• Вращающий момент, действующий на контур с током, помещенный в однородное магнитное поле,
 ,
,
где  - угол между направлением нормали к плоскости контура и магнитной индукцией поля.
- угол между направлением нормали к плоскости контура и магнитной индукцией поля.
• Сила взаимодействия между двумя прямолинейными параллельными проводниками с токами  и
и 
 ,
,
где  - длина проводника,
- длина проводника,  - расстояние между ними.
- расстояние между ними.
• Магнитный поток через площадку 
 ,
,
где  ,
,  - угол между направлением вектора магнитной индукции и нормалью к площадке
- угол между направлением вектора магнитной индукции и нормалью к площадке  .
.
• Магнитный поток неоднородного поля через произвольную поверхность
 ,
,
где интегрирование ведется по всей поверхности.
• Магнитный поток однородного поля через плоскую поверхность
 .
.
• Работа перемещения проводника с током в магнитном поле
 ,
,
где  - поток магнитной индукции, пересеченный проводником при его движении.
- поток магнитной индукции, пересеченный проводником при его движении.
• Сила Лоренца, действующая на движущуюся заряженную частицу в магнитном поле,
 ,
,
где  - заряд частицы,
- заряд частицы, 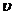 - скорость частицы,
- скорость частицы,  - угол между направлениями скорости частицы и магнитной индукции поля.
- угол между направлениями скорости частицы и магнитной индукции поля.
• Э.Д.С. индукции

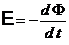 .
.
• Разность потенциалов на концах проводника, движущегося в магнитном поле,
 ,
,
где 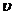 - скорость движения проводника,
- скорость движения проводника,  - длина проводника,
- длина проводника,  - угол между направлениями скорости движения проводника и магнитной индукцией поля.
- угол между направлениями скорости движения проводника и магнитной индукцией поля.
• Э.Д.С. самоиндукции
 ,
,
где  - индуктивность контура.
- индуктивность контура.
• Индуктивность соленоида
 ,
,
где 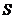 - площадь поперечного сечения соленоида,
- площадь поперечного сечения соленоида,  - длина соленоида,
- длина соленоида,  - полное число витков.
- полное число витков.
• Энергия магнитного поля контура с током
 .
.
• Объемная плотность энергии магнитного поля

 .
.
 3.1. На рис. 3.1 изображено сечение двух прямолинейных бесконечно длинных проводников с током. Расстояние АС между проводниками равно 10 см, I1=20 А, I2 = 30 А. Найти магнитную индукцию поля, вызванного токами I1 и I2 в точках М1, М2 и М3. Расстояния М1А=2 см, АМ2 =4 см и СМ3 =3 см.
3.1. На рис. 3.1 изображено сечение двух прямолинейных бесконечно длинных проводников с током. Расстояние АС между проводниками равно 10 см, I1=20 А, I2 = 30 А. Найти магнитную индукцию поля, вызванного токами I1 и I2 в точках М1, М2 и М3. Расстояния М1А=2 см, АМ2 =4 см и СМ3 =3 см.
Рис. 3.1.
А.[0,15мТл; 0,20 мТл; 0,17 мТл] В.[150мТл; 200 мТл; 170 мТл]
С. [150 мкТл; 200 мкТл; 170 мкТл] D. [1,5 мТл; 2,0 мТл; 1,7 мТл]
3.2. Решить предыдущую задачу при условии, что токи текут в одном
направлении.
А. [0,25 мТл; 0; 0,23 мТл] В. [25 мкТл; 0; 23 мкТл]
С. [0; 250 мТл; 230 мТл] D. [2,5 мТл; 2,3 мкТл; 0]
3.3. Два прямолинейных бесконечно длинных проводника расположены перпендикулярно друг к другу и находятся в одной плоскости (рис. 3.2). Найти магнитную индукцию поля в точках М1 и М2, если I1=2 А и I2=3 А. Расстояния АМ1=АМ2= 1 см, DМ1=СМ2=2 см.
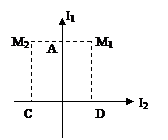 |  | ||
Рис. 3.2 Рис. 3.3
А. [10ˉ5 Тл; 7·10ˉ5 Тл ] В. [10ˉ7 Тл; 7·10ˉ7 Тл]
С. [10 мТл; 70 мТл] D. [1 мТл; 7 мТл]
3.4. Два прямолинейных бесконечно длинных проводника расположены перпендикулярно друг к другу и находятся во взаимно-перпендикулярных плоскостях (рис. 3.3). Найти магнитную индукцию поля в точках М1 и М2, если I1=2 А и I2=3 А. Расстояния АМ1=АМ2= 1 см и АС=2 см.
А. [4,5·10ˉ5 Тл; 7,2·10ˉ5 Тл] В. [7·10ˉ7Тл; 7·10ˉ7Тл]
С. [4,5 мТл; 7,2 мТл] D. [45 мТл; 72 мТл]
3.5. На рис. 3.4 изображено сечение трёх прямолинейных бесконечно длинных проводников с током. Расстояния АС=СD=5 см; I1=I2=I; I3=2I. Найти точку на прямой АD, в которой индукция магнитного поля, вызванного токами I1, I2, I3, равна нулю.
 |
Рис. 3.4
A.[3,3 см от I1 вправо] B.[3,3 см от I1 влево]
С.[3,3 см от I2 вправо] D.[3,3 см от I3 влево]
3.6. Решить предыдущую задачу при условии, что все токи текут в одном направлении.
A.[1,8 см и 6,96 см от точки А вправо] B.[1,8 см от точки А вправо]
C.[1,8 см и 6,96 см от точки С вправо] D.[6,96 см от точки с влево]
3.7. Два круговых витка радиусом 4 см каждый расположены в параллельных плоскостях на расстоянии 0,1 м друг от друга. По виткам текут токи I1= I2=2 А. Найти магнитную индукцию поля на оси витков в точке, находящейся на равном расстоянии от них. Токи в витках текут в одном направлении.
А. [1,5·10ˉ5 Тл] B.[1,5мк Тл] С. [0] D. [15 мТл]
3.8. Решить предыдущую задачу при условии, что токи текут в противоположных направлениях.
А. [0] В. [1,5·10ˉ5 Тл] С. [1,5мТл] D. [15 мТл]
3.9. Ток в 2А течет по длинному проводнику, согнутому под углом  . Найти магнитную индукцию поля в точке, лежащей на биссектрисе этого угла и отстоящей от вершины угла на расстоянии 10 см.
. Найти магнитную индукцию поля в точке, лежащей на биссектрисе этого угла и отстоящей от вершины угла на расстоянии 10 см.
А. [6,9 мкТл] В. [3,5 мкТл] С. [0 мкТл] D. [8,0 мкТл]
3.10. По проводнику, согнутому в виде прямоугольника со сторонами а = 8 см и в = 12 см, течет ток силой I = 50 А. Определить напряженность и магнитную индукцию поля в точке пересечения диагоналей прямоугольника.
А. [478 А/м; 0,6 мТл] В. [434 А/м; 1,1 мТл]
С. [0 А/м; 0 мТл] D. [241 А/м; 0,3 мТл]
3.11. По проволочной рамке, имеющей форму правильного шестиугольника, течет ток силой I = 2 А. При этом в центре рамки образуется магнитное поле В = 41,4 мкТл. Найти длину проволоки, из которой сделана рамка.
А. [0,2 м] В. [0,6 м] С. [0,03 м] D. [0,1 м]
3.12. По проводнику, изогнутому в виде окружности, течет ток. Магнитное поле в центре окружности В = 6,28 мкТл. Не изменяя силу тока в проводнике, ему придали форму квадрата. Определить магнитную индукцию поля в точке пересечения диагоналей этого квадрата.
А. [7,2 мкТл] В. [22,6 мк С. [72 мкТл] D. [72 мТл]
3.13. Обмотка соленоида содержит два слоя плотно прилегающих друг к другу витков провода диаметром d = 0,2 мм. Определить магнитную индукцию поля на оси соленоида, если по проводу течет ток I = 0,5 А.
А. [6,28 мТл] В. [6,28 мкТл] С. [3,14 мТл] D. [3,14 мкТл]
3.14. Тонкое кольцо массой 15 г и радиусом 12 см несет заряд, равномерно распределенный с линейной плотностью 10 нКл/м. Кольцо равномерно вращается с частотой 8 с-1 относительно оси, перпендикулярной плоскости кольца и проходящей через ее центр. Определить отношение магнитного момента кругового тока, создаваемого кольцом, к его моменту импульса.
А. [251 нКл/кг] В. [25 мкКл/кг] С. [0,5 мкКл/кг] D. [31 нКл/кг]
3.15. По двум бесконечно длинным прямым параллельным проводникам, расстояние между которыми равно 25 см, текут токи 20 и 30 А в противоположных направлениях. Определить магнитную индукцию поля в точке, удаленной на расстояние 30 см от первого и 40 см от второго проводника.
А. [9,5 мкТл] В. [1,9 мкТл] С. [6,7 мкТл] D. [ 27,0 мкТл]
3.16. Определить магнитную индукцию поля на оси тонкого проволочного кольца радиусом 10 см, по которому течет ток 10 А, в точке, расположенной на расстоянии 15 см от центра кольца.
А. [10,7 мкТл] В. [10,7 нТл] С. [6,8 мкТл] D. [3,4 мкТл]
3.17. По проводу, согнутому в виде квадрата со стороной, равной 60 см, течет постоянный ток 3 А. Определить магнитную индукцию поля в центре квадрата.
А. [5,66 мкТл] В. [0 мкТл] С. [56,6 мкТл] D. [2,83 мкТл]
3.18. Ток, протекая по проволочному кольцу из медной проволоки сечением 1,0 мм2, создает в центре кольца магнитную индукцию поля 0,224 мТл. Разность потенциалов, приложенная к концам проволоки, образующей кольцо, равна 0,12 В. Какой ток течет по кольцу?
А. [20 А] В. [200 А] С. [ 2 А] D. [6 А]
3.19. Ток 2 А, протекая по катушке длиной 30 см, создает внутри нее магнитную индукцию поля 8,38 мТл. Сколько витков содержит катушка? Диаметр катушки считать малым по сравнению с ее длиной.
А. [1000] В. [6672] С. [10000] D. [11111]
3.20. Бесконечно длинный провод образует круговую петлю, касательную к проводу. Радиус петли равен 8 см. По проводу течет ток силой 5А. Найти индукцию магнитного поля в центре петли.
А. [51,8 мкТл] В. [7,9 мкТл] С. [91,0 мкТл] D. [25,0 мкТл]
3.21*. Найти распределение магнитной индукции поля вдоль оси кругового витка диаметром 10 см, по которому течет ток силой 10А. Составить таблицу значений  для значений
для значений  в интервале 0
в интервале 0  10 см через каждые 2 см и построить график с нанесением масштаба. [
10 см через каждые 2 см и построить график с нанесением масштаба. [  ]
]  .
.
3.22*. Определить, пользуясь теоремой о циркуляции вектора  , магнитную индукцию поля на оси тороида без сердечника, по обмотке которого, содержащей 300 витков, протекает ток 1А. Внешний диаметр тороида равен 60 см, внутренний – 40 см. [0,24 мТл].
, магнитную индукцию поля на оси тороида без сердечника, по обмотке которого, содержащей 300 витков, протекает ток 1А. Внешний диаметр тороида равен 60 см, внутренний – 40 см. [0,24 мТл].
3.23. Два бесконечных прямолинейных параллельных проводника с одинаковыми токами, текущими в одном направлении, находятся друг от друга на расстоянии R. Чтобы их раздвинуть до расстояния 3R, на каждый сантиметр длины проводника затрачивается работа 220 нДж. Определить силу тока в проводниках.
А. [10А] В. [3,2А] С. [5А] D. [100А]
3.24. Прямой проводник длиной 20 см, по которому течет ток 40А, находится в однородном магнитном поле с индукцией 0,5 Тл. Какую работу совершают силы поля, перемещая проводник на 20 см, если направление движения перпендикулярно линиям магнитной индукции и проводнику.
А. [0,8 Дж] В. [80 Дж] С. [8000 Дж] D. [0 Дж ]
3.25. В однородном магнитном поле, индукция которого 0,5 Тл, движется равномерно проводник со скоростью 20 см/с перпендикулярно полю. Длина проводника 10 см. По проводнику течет ток 2А. Найти мощность, затрачиваемую на перемещение проводника.
А. [20 мВт] B.[2 Вт] С.[200 Вт] D. [0 Вт]
3.26. Магнитная индукция однородного поля 0,4 Тл. В этом поле равномерно со скоростью 15 см/с движется проводник длиной 1 м так, что угол между проводником и индукцией поля равен 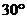 . По проводнику течет ток 1А. Найти работу перемещения проводника за 10 с движения.
. По проводнику течет ток 1А. Найти работу перемещения проводника за 10 с движения.
А. [0,3 Дж] В. [30 Дж] С. [5,1 Дж] D. [51 Дж]
3.27. Проводник длиной 1м расположен перпендикулярно однородному магнитному полю с индукцией 1,3 Тл. Определить ток в проводнике, если при движении его со скоростью 10 см/с в направлении, перпендикулярном
полю и проводнику, за 4 с на перемещение проводника расходуется энергия 10 Дж.
А. [19А] В. [1,9 кА] С. [32А] D. [0,19А]
3.28. В однородном магнитном поле с индукцией 18 мкТл в плоскости, перпендикулярной линиям индукции, расположена плоская круговая рамка, состоящая из 10 витков площадью 100 см2 каждый. В обмотке рамки течет ток 3А. Каково должно быть направление тока в рамке, чтобы при повороте ее на  вокруг одного из диаметров силы поля совершили положительную работу? Какова величина этой работы?
вокруг одного из диаметров силы поля совершили положительную работу? Какова величина этой работы?
А. [1,08 мкДж] В. [10,8 мДж ] С. [5,4 мДж] D. [0 Дж]
3.29. Квадратный контур со стороной 20 см, по которому течет ток 20А, свободно установился в однородном магнитном поле с индукцией 10 мТл. Определить изменение потенциальной энергии контура при повороте вокруг оси, лежащей в плоскости контура, на угол  .
.
А. [16 мДж] В. [16 Дж] С. [1,6 Дж] D. [8 Дж]
3.30. По круговому витку радиусом 15 см течет ток силой 10А. Виток расположен в однородном магнитном поле с индукцией 40 мТл так, что нормаль к плоскости контура составляет угол 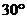 с вектором магнитной индукции. Определить изменение потенциальной энергии контура при его повороте на угол
с вектором магнитной индукции. Определить изменение потенциальной энергии контура при его повороте на угол  в направлении увеличения угла.
в направлении увеличения угла.
А.[0,04 Дж] В. [0,03 Дж] С. [0,4 Дж] D. [0,3 Дж]
3.31. Круглая рамка с током площадью 20 см2 закреплена параллельно магнитному полю с индукцией 0,2 Тл, и на нее действует вращающий момент 0,6 мН·м. Когда рамку освободили, она повернулась на  и ее угловая скорость стала 20 с-1. Определить силу тока, текущего в рамке.
и ее угловая скорость стала 20 с-1. Определить силу тока, текущего в рамке.
А. [1,5А] В. [1,5 мА] С. [0,15А] D. [ 15 А]
3.32. Два длинных горизонтальных проводника расположены параллельно друг другу на расстоянии 8 мм. Верхний проводник закреплен неподвижно, а нижний висит свободно под ним. Какой ток нужно пропустить по верхнему проводу для того, чтобы нижний мог висеть, не падая? По нижнему течет ток в 1А и масса каждого сантиметра длины проводника равна 2,55 мг.
А. [100А] В. [200А] С. [0,2А] D. [0,1А]
3.33. Поток магнитной индукции сквозь площадь поперечного сечения соленоида (без сердечника) 5 мкВб. Длина соленоида 35 см. Определить магнитный момент этого соленоида.
А. [1А·м2] В. [10А·м2] С. [0,1А·м2] D. [0,01А·м2]
3.34. Круговой контур помещен в однородное магнитное поле так, что плоскость контура перпендикулярна силовым линиям поля. Магнитная индукция поля 0,2 Тл. По контуру течет ток 2А. Радиус контура 2 см. Какая работа совершится при повороте контура на  ?
?
А. [50 мДж] В. [5 мДж] С. [0 Дж] D. [1 мДж]
3.35*. Рядом с длинным прямым проводом, по которому течет ток 30А, расположена квадратная рамка с током 2А. Рамка и провод лежат в одной плоскости. Проходящая через середины противоположных сторон ось рамки параллельна проводу и отстоит от него на расстоянии 30 мм. Сторона рамки 20 мм. Найти работу, которую нужно совершить, чтобы повернуть рамку вокруг ее оси на  . [0,33 мкДж].
. [0,33 мкДж].
3.36*. Два прямолинейных длинных проводника находятся на расстоянии 10 см друг от друга. По проводникам текут токи 20А и 30А. Какую работу на единицу длины проводников надо совершить, чтобы раздвинуть эти проводники до расстояния 20 см? [83 мкДж].
3.37. Протон, ускоренный разностью потенциалов 0,5 кВ, влетая в однородное магнитное поле с индукцией 0,1 Тл, движется по окружности. Определить радиус этой окружности.
А. [3,23 см] В. [1,0 см] С. [32 см] D. [10 см]
3.38. Альфа-частица со скоростью 2Мм/с влетает в магнитное поле с индукцией 1 Тл под углом 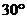 . Определить радиус витка винтовой линии, которую будет описывать альфа-частица?
. Определить радиус витка винтовой линии, которую будет описывать альфа-частица?
А. [2,1 см] В. [4,2 см] С. [8,4 см] D. [21,0 см]
3.39. Магнитное поле с индукцией 126 мкТл направлено перпендикулярно электрическому полю, напряженность которого 10 В/м. Ион, летящий с некоторой скоростью, влетает в эти скрещенные поля. При какой скорости он будет двигаться прямолинейно?
А. [79 км/с] В. [79 Мм/с] С. [0,79 км/с] D. [7,9 Мм/с]
3.40. Электрон, ускоренный разностью потенциалов 6 кВ, влетает в однородное магнитное поле под углом 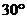 к направлению поля и начинает двигаться по винтовой линии. Магнитная индукция поля равна 130 мТл. Найти шаг винтовой линии.
к направлению поля и начинает двигаться по винтовой линии. Магнитная индукция поля равна 130 мТл. Найти шаг винтовой линии.
А. [11 см] В. [2,2 см] С. [ 1,1 см] D. [22 см]
3.41. Протон влетел в однородное магнитное поле под углом 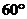 к направлению линий поля и движется по спирали, радиус которой 2,5 см. магнитная индукция поля равна 0,05 Тл. Найти кинетическую энергию протона.
к направлению линий поля и движется по спирали, радиус которой 2,5 см. магнитная индукция поля равна 0,05 Тл. Найти кинетическую энергию протона.
А. [1,6·10-17 Дж] В. [3,2·10-17 Дж ]
С. [6,4·10-17 Дж ] D. [3,2·10-2 Дж ]
3.42. Определить частоту обращения электрона по круговой орбите в магнитном поле с индукцией 1 Тл. Как изменится частота обращения, если вместо электрона будет вращаться альфа-частица?
А. [28 ГГц; уменьшится в 3648 раз]
В. [2,8 ТГц; уменьшится в 3426 раз]
С. [28 ТГц; увеличится в 3648 раз]
D. [2,8 МГц; увеличится в 3426 раз]
3.43. Протон и альфа-частица, ускоренные одинаковой разностью потенциалов, влетают в однородное магнитное поле. Во сколько раз радиус кривизны траектории протона меньше радиуса кривизны траектории альфа-частицы?
А. [1,4] В. [0,7] С. [2] D. [0,5]
3.44. Частица, несущая один элементарный заряд, влетела в однородное магнитное поле с индукцией 0,05 Тл. Определить момент импульса, которым обладала частица при движении в магнитном поле, если траектория ее представляла дугу окружности радиусом 0,2 мм.
А. [3,2·10-28 Н·м·с] В. [1,6·10-24 Н·м·с]
С. [1,6·10-23 Н·м·с] D. [3,2·10-27 Н·м·с]
3.45. Электрон движется по окружности в однородном магнитном поле с индукцией 31,4 мТл. Определить период обращения электрона.
А. [1,1 нс] В. [0,2 нс] С. [0,4 нс] D. [2 нс]
3.46. Найти отношение q/m для заряженной частицы, если она, влетая со скоростью 108 см/с в однородное магнитное поле напряженностью в 2·105 А/м, движется по дуге окружности радиусом 8,3 см. Направление скорости движения частицы перпендикулярно направлению магнитного поля.
А. [48 МКл/кг] В. [4,8 МКл/кг] С. [60 Кл/кг] D. [6 Кл/кг]
3.47. Электрон, ускоренный разностью потенциалов 3 кВ, влетает в магнитное поле соленоида под углом 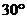 к его оси. Число ампер-витков соленоида равно 5000. Длина соленоида 26 см. Найти шаг винтовой траектории электрона в магнитном поле соленоида.
к его оси. Число ампер-витков соленоида равно 5000. Длина соленоида 26 см. Найти шаг винтовой траектории электрона в магнитном поле соленоида.
А. [3,94 см] В. [3,94 мм] С. [0,394 м] D. [3,94 м]
3.48. Заряженная частица движется в магнитном поле по окружности со скоростью 1 Мм/с. Магнитная индукция поля равна 0,3 Тл. Радиус окружности 4 см. Найти заряд частицы, если известно, что ее кинетическая энергия равна 12 кэВ.
А. [3,2·10-19 Кл] В. [1,6·10-19 Кл]
С. [3,2·10-22 Кл] D. [1,6·10-22 Кл]
3.49*. Серпуховской ускоритель протонов ускоряет эти частицы до энергии 76 Гэв. Если отвлечься от наличия ускоряющихся промежутков, то можно считать, что ускоренные протоны движутся по окружности радиуса 236 м и удерживаются на ней магнитным полем, перпендикулярным к плоскости орбиты. Найти необходимое для этого магнитное поле. [1,07 кТл].
3.50*. Заряженная частица прошла ускоряющую разность потенциалов 104 В и влетела в скрещенные под прямым углом электрическое (Е = 100 В/м) и магнитное (В = 0,1 Тл) поля. Определить отношение заряда частицы к ее массе, если, двигаясь перпендикулярно обоим полям, частица не испытывает отклонений от прямолинейной траектории. [4,8 кКл/кг].
3.51. В однородном магнитном поле с индукцией 0,1 Тл равномерно вращается рамка, содержащая 1000 витков. Площадь рамки 150 см2. Рамка делает 10 об/с. Определить максимальную э.д.с. индукции в рамке. Ось вращения лежит в плоскости рамки и перпендикулярна направлению поля.
А. [94,2 В] В. [15 В] С. [0,1 В] D. [1,5 В]
3.52. Проволочный виток расположен перпендикулярно магнитному полю, индукция которого изменяется по закону В=Во(1+екt), где Во = 0,5 Тл, к =1 с-1. Найти величину э.д.с., индуцируемой в витке в момент времени, равный 2,3 с. Площадь витка 0,04 м2.
А. [2 мВ] В. [0 В] С. [2 В] D. [0,02 В]
3.53. В магнитном поле с индукцией 0,1 Тл помещена квадратная рамка из медной проволоки. Площадь поперечного сечения проволоки 1 мм2, площадь рамки 25 см2. Нормаль к плоскости рамки параллельна силовым линиям поля. Какой заряд пройдет по рамке при исчезновении магнитного поля? Удельное сопротивление меди 17 нОм·м.
А. [74 мКл] В. [3,6 Кл] С. [296 Кл] D. [0,36 Кл]
3.54. Кольцо из алюминиевого провода помещено в магнитное поле перпендикулярно линиям магнитной индукции. Диаметр кольца 20 см, диаметр провода 1 мм. Определить скорость изменения магнитного поля, если сила индукционного тока в кольце 0,5А. Удельное сопротивление алюминия 26 нОм·м.
А. [0,33 Тл/с] В. [1,7 мТл/с] С. [0,08 Тл/с] D. [0,4 мТл/с]
3.55. В магнитном поле, индукция которого 0,25 Тл, вращается стержень длиной 1 м с постоянной угловой скоростью 20 рад/с. Ось вращения проходит через конец стержня параллельно силовым линиям поля. Найти э.д.с. индукции, возникающую на концах стержня.
А. [2,5 В] В. [5 В] С. [25 В] D. [0,5 В]
3.56. Кольцо из проволоки сопротивлением 1 мОм находится в однородном магнитном поле с индукцией 0,4 Тл. Плоскость кольца составляет с линиями индукции угол  . Определить заряд, который протечет по кольцу, если его выдернуть из поля. Площадь кольца равна 10 см2.
. Определить заряд, который протечет по кольцу, если его выдернуть из поля. Площадь кольца равна 10 см2.
А. [0,4 Кл] В. [4 мКл] С. [4 Кл] D. [4 мкКл]
3.57. Катушка, содержащая 10 витков, каждый площадью 4 см2, находится в однородном магнитном поле. Ось катушки параллельна линиям индукции поля. Катушка присоединена к баллистическому гальванометру с сопротивлением 1000 Ом, сопротивлением катушки можно пренебречь. Когда катушку выдернули из поля, через гальванометр протекло 2 мкКл. Определить индукцию поля.
А. [0,5 Тл] В. [5 Тл] С. [50 Тл] D. [0,05 Тл]
3.58. На стержень из немагнитного материала длиной 50 см и сечением 2 см2 намотан в один слой провод так, что на каждый сантиметр длины стержня приходится 20 витков. Определить энергию магнитного поля соленоида, если сила тока в обмотке 0,5А.
А. [20 мкДж] В. [20 мДж] С. [2 Дж] D. [0,2 Дж]
3.59. Найти разность потенциалов на концах оси автомобиля, возникающую при горизонтальном движении его со скоростью 120 км/ч, если длина оси 1,5 м и вертикальная составляющая напряженности земного магнитного поля равна 40А/м.
А. [2,5 мВ] В. [9 мВ] С. [9 В] D. [2,5 В]
3.60. На соленоид длиной 20 см и площадью поперечного сечения 30 см2 надет проволочный виток. Обмотка соленоида имеет 320 витков и по ней течет ток 3А. Какая э.д.с. индуцируется в надетом на соленоид витке, когда ток в соленоиде исчезает в течение 0,001 с?
А. [18 мВ] В. [1,8 мВ] С. [ 0,18 В] D. [18 В]
3.61. Катушка диаметром 10 см, имеющая 500 витков, находится в магнитном поле. Ось катушки параллельна линиям магнитной индукции поля. Чему равно среднее значение э.д.с. индукции в катушке, если магнитная индукция поля увеличивается в течение 0,1 с от нуля до 2 Тл?
А. [78,5 В] В. [0,16 В] С. [314 В] D. [25 В]
3.62*. Маховое колесо диаметром 3 м вращается вокруг горизонтальной оси со скоростью 3000 об/мин. Определить э.д.с., индуцируемую между ободом и осью колеса, если плоскость колеса составляет с плоскостью магнитного меридиана угол 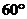 . Горизонтальная составляющая земного магнитного поля равна 20 мкТл. [3,5 мВ].
. Горизонтальная составляющая земного магнитного поля равна 20 мкТл. [3,5 мВ].
3.63*. Медный обруч, имеющий массу 5 кг, расположен в плоскости магнитного меридиана. Какой заряд индуцируется в нем, если его повернуть около вертикальной оси на  ? Горизонтальная составляющая земного магнитного поля 20 мкТл. Плотность меди 8900 кг/м3, удельное сопротивление меди 17 нОм ·м. [5,26 мКл].
? Горизонтальная составляющая земного магнитного поля 20 мкТл. Плотность меди 8900 кг/м3, удельное сопротивление меди 17 нОм ·м. [5,26 мКл].
3.64*. В однородном магнитном поле, индукция которого 0,5 Тл, равномерно с частотой 300 мин-1  вращается катушка, содержащая 200 витков, плотно прилегающих друг к другу. Площадь поперечного сечения катушки 100 см2. Ось вращения перпендикулярна оси катушки и направлению магнитного поля. Определить максимальную э.д.с., индуцируемую в катушке. [31,4 В].
вращается катушка, содержащая 200 витков, плотно прилегающих друг к другу. Площадь поперечного сечения катушки 100 см2. Ось вращения перпендикулярна оси катушки и направлению магнитного поля. Определить максимальную э.д.с., индуцируемую в катушке. [31,4 В].
Не нашли, что искали? Воспользуйтесь поиском: