для студентов заочной формы обучения. Решение. По правилу действия над матрицами

Образцы с решениями

Пример 1. Даны матрицы:

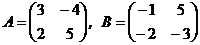. Найти матрицу .

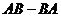Решение. По правилу действия над матрицами

.

.

.

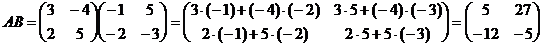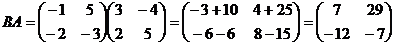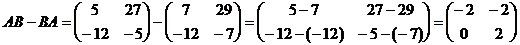Пример 2. Вычислить определитель .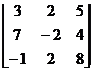

Решение. Вычислим определитель, разлагая его, например, по первой строке

.

Пример 3. Решить систему уравнений методом Крамера:

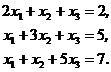
Решение. Найдем определитель основной матрицы:

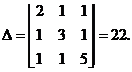Так как , то система крамеровская. Найдем вспомогательные определители

.

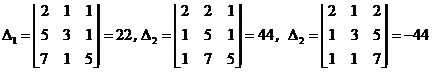Значит,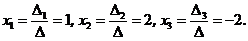

Пример 4. Проверить, что векторы 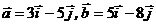линейно независимы. Разложить вектор 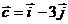по векторам 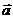и .

Решение. Система, состоящая из двух векторов, линейно зависима тогда и только тогда, когда эти векторы коллинеарны или координаты векторов пропорциональны, или определитель, составленный из координат векторов равен нулю.

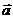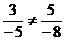Координаты векторов и не пропорциональны: , следовательно, система 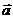, линейно независима, значит, на плоскости они образуют базис. Поэтому вектор 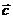можно разложить по векторам 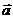и .

Разложить векторов 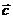по векторам 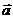и означает: найти числа 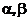такие, что

. Или в координатной форме: . Так как два вектора равны тогда и только тогда, когда у них равны соответствующие координаты, то имеем систему уравнений

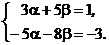
Решая ее по методу Крамера, находим:

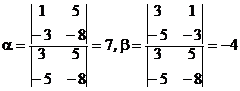. Таким образом, .

Пример 5. Найти угол 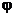между векторами и 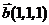в трехмерном пространстве.

Решение. По определению скалярного произведению векторов . Отсюда

. Значит, .

Пример 6. Найти площадь треугольника 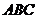, если .

Решение. Треугольник 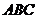составляет половину трапеции . Найдем координаты векторов 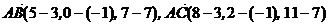, то есть, 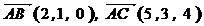. Как известно, модуль векторного произведения векторов равен площади параллелограмма, построенного на векторах, как на сторонах.

Найдем векторное произведение векторов:

.

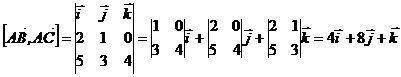Тогда 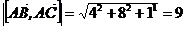. Площадь треугольника .

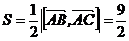Пример 7. Найти объем пирамиды, вершины которой находятся в точках , .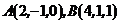

Решение. Найдем координаты векторов 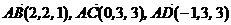. Вычислим смешанное произведение векторов

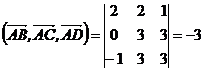. Как известно, модуль смешанного произведения трех векторов равен объему параллелепипеда, построенного на векторах как на сторонах. А объем пирамиды составляет шестую часть объема параллелепипеда, поэтому объем пирамиды равен .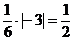

Пример 8. Написать уравнение прямой, проходящей через точк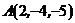и и .

Решение. Каноническое уравнение прямой, заданной двумя точками имеет вид

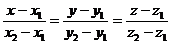. Подставив координаты данных точек в это уравнение, получим 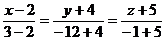, то есть, .

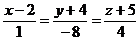Пример 9. Составить уравнение плоскости, проходящей через прямую 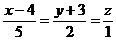и точку .

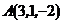Решение. Из уравнения прямой видно, что она задается точкой 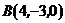и вектором 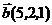. Найдем координаты вектора .

Уравнение плоскости, заданной точкой и двумя векторами, имеет вид

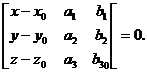Подставив данные из задачи, получим уравнение искомой плоскости

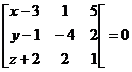. Или разложив определитель по первому столбцу, имеем 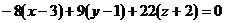или .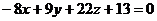

Пример 10. Вычислить предел .

Решение. Это неопределенность вида 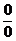, в которых участвуют тригонометрические функции. Такие неопределенности часто раскрываются с помощью первого замечательного предела .

.

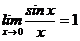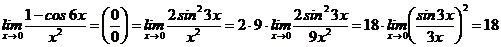Пример 11. Найти производную функции 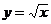. Чему равно значение ?

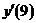Решение. Перепишем функцию в другом виде 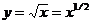. По таблице производных находим: если 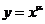, то . В рассматриваем случае 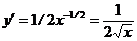. Отсюда при имеем .

Пример 12. Найти: а) промежутки возрастания и убывания; б) экстремумы функции; в) промежутки выпуклости и вогнутости, точки перегиба следующей функции:

.

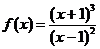Решение. .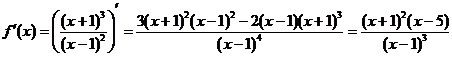

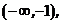
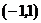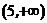Отсюда видим, что производная равна нулю в точках , и не существует при . Функция определена только в точке . Так как в этой точке производная функции меняет знак с минуса на плюс, то это точка – точка минимума (экстремум). В промежутках и производная положительна, значит, функция возрастает; а в промежутке производная отрицательна, значит, функция убывает.

в) Найдем производную второго порядка

. Замечаем, вторая производная равна нулю в точке и не существует при . Эти точки разбивают всю числовую прямую на три област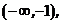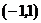и и 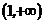. В первом и третьем промежутках вторая производная отрицательна, а во втором промежутке – положительна. Следовательно, в первом и третьем промежутках функция вогнута, а во втором промежутке функция выпукла. В точке функция 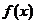определена, и вторая производная при переходе через эту точку меняет знак с плюса на минус, следовательно, точка есть точка перегиба.

Пример 13. Вычислить интеграл:

а) 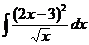; б) ; в) .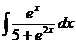

Решение. а) Преобразуем подынтегральное выражение, воспользуемся свойством линейности интеграла:

.

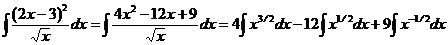Все полученные интегралы – табличные: . Поэтому .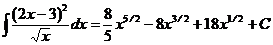

б) Преобразуем интеграл, используя прием введения под знак дифференциала

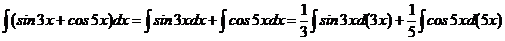. Полученные интегралы снова табличные. Применяя табличные формулы, получим

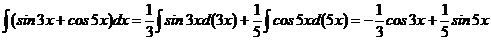+С.

в) Заметим, что 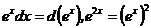. Произведем замену переменной :

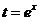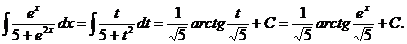
Вариант 1.

1. Даны матрицы:

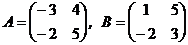. Найти матрицу .

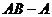2. Вычислить определитель .

3. Решить систему уравнений методом Крамера:

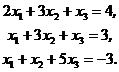
4. Проверить, что векторы 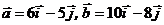линейно независимы. Разложить вектор 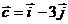по векторам 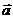и .

5. Найти угол 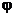между векторам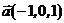и и 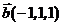в трехмерном пространстве.

6. Найти площадь треугольника 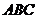, если .

7. Найти объем пирамиды, вершины которой находятся в точках , .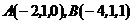

8. Написать уравнение прямой, проходящей через точк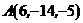и и .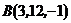

9. Составить уравнение плоскости, проходящей через прямую 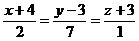и точку .

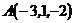10. Вычислить предел .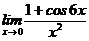

11. Найти производную функции . Чему равно значение ?

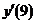12. Найти: а) промежутки возрастания и убывания; б) экстремумы функции; в) промежутки выпуклости и вогнутости, точки перегиба следующей функции:

.

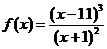13. Вычислить интеграл:

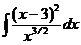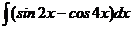а) ; б) ; в) .

Вариант 2.

1. Даны матрицы:

. Найти матрицу .

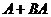2. Вычислить определитель .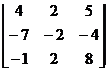

3. Решить систему уравнений методом Крамера:

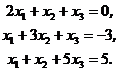
4. Проверить, что векторы 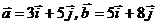линейно независимы. Разложить вектор 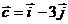по векторам 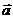и .

5. Найти угол 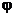между векторами и 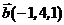в трехмерном пространстве.

6. Найти площадь треугольника 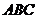, если .

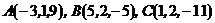7. Найти объем пирамиды, вершины которой находятся в точках , .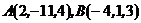

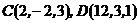8. Написать уравнение прямой, проходящей через точк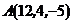и и .

9. Составить уравнение плоскости, проходящей через прямую 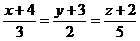и точку .

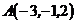10. Вычислить предел .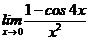

11. Найти производную функции 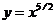. Чему равно значение ?

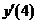12. Найти: а) промежутки возрастания и убывания; б) экстремумы функции; в) промежутки выпуклости и вогнутости, точки перегиба следующей функции:

.

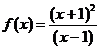13. Вычислить интеграл:

а) ; б) ; в) .

Вариант 3.

1. Даны матрицы:

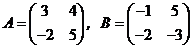. Найти матрицу .

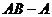2. Вычислить определитель .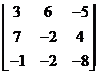

3. Решить систему уравнений методом Крамера:

4. Проверить, что векторы 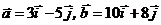линейно независимы. Разложить вектор 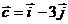по векторам 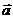и .

5. Найти угол 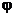между векторам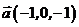и и 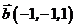в трехмерном пространстве.

6. Найти площадь треугольника 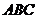, если .

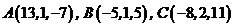7. Найти объем пирамиды, вершины которой находятся в точках , .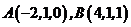

8. Написать уравнение прямой, проходящей через точки и .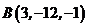

9. Составить уравнение плоскости, проходящей через прямую 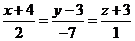и точку .

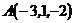10. Вычислить предел .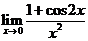

11. Найти производную функции . Чему равно значение ?

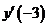12. Найти: а) промежутки возрастания и убывания; б) экстремумы функции; в) промежутки выпуклости и вогнутости, точки перегиба следующей функции:

.

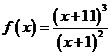13. Вычислить интеграл:

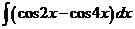а) ; б) ; в) .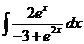

Вариант 4.

1. Даны матрицы:

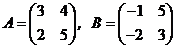. Найти матрицу .

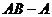2. Вычислить определитель .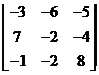

3. Решить систему уравнений методом Крамера:

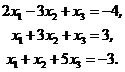
4. Проверить, что векторы 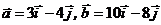линейно независимы. Разложить вектор 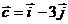по векторам 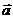и .

5. Найти угол 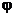между векторам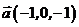и и 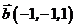в трехмерном пространстве.

6. Найти площадь треугольника 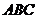, если .

7. Найти объем пирамиды, вершины которой находятся в точках , .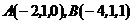

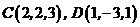8. Написать уравнение прямой, проходящей через точк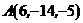и и .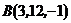

9. Составить уравнение плоскости, проходящей через прямую 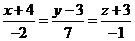и точку .

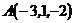10. Вычислить предел .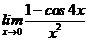

11. Найти производную функции . Чему равно значение ?

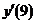12. Найти: а) промежутки возрастания и убывания; б) экстремумы функции; в) промежутки выпуклости и вогнутости, точки перегиба следующей функции:

.

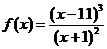13. Вычислить интеграл:

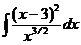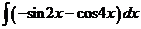а) ; б) ; в) .

Не нашли, что искали? Воспользуйтесь поиском: