Методика и техника эксперимента. В данной работе рассматриваются вынужденные электромагнитные колебания, возникающие в колебательном контуре под действием внешней периодически изменяющейся

В данной работе рассматриваются вынужденные электромагнитные колебания, возникающие в колебательном контуре под действием внешней периодически изменяющейся ЭДС.

ЭДС источника, подключенного к колебательному контуру, изменяется по гармоническому закону:

E = E ₀ cosωt. (6.12)

Выведем уравнение вынужденных колебаний, возникающих в колебательном контуре, состоящем из последовательно соединенных конденсатора С и катушки индуктивности L, подключенных к источнику ЭДС.

Полагая, что мгновенные значения тока в контуре и напряжений на обкладках конденсатора U с и катушки индуктивности U _L удовлетворяют законам, установленным для цепей постоянного тока, применим к колебательному контуру второй закон Кирхгофа: алгебраическая сумма падений напряжений в замкнутом контуре равна алгебраической сумме ЭДС, действующих в этом контуре:

I · R + U_с = E _s + E. (6.13)

Так как: U _С = 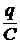– падение напряжения на обкладках конденсатора;

E_s = – L – ЭДС самоиндукции;

E = E ₀ sinωt – внешняя ЭДС,

уравнение (6.13) примет вид:

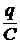+ I·R + L = E ₀ sin ωt. (6.14)

Изменения тока I и напряжения U с течением времени должны происходить с той же частотой ω, с какой изменяется внешняя ЭДС, однако фаза колебаний этих величин может отличаться от фазы колебаний ЭДС.

Продифференцируем уравнение (6.14) по времени и разделим на величину L. В результате получим уравнение вынужденных колебаний:

+ + t. (6.15)

Решение этого уравнения будет иметь вид:

I = I₀ sin (ωt – φ). (6.16)

Соответствующие расчеты приводят к следующим значениям для амплитуды тока и разности фаз между током и внешней ЭДС:

– амплитуда тока, (6.17)

tg φ = – разность фаз между током I и E. (6.18)

Таким образом, амплитуда тока в контуре зависит от сопротивления контура R и соотношения между параметрами контура L, С и частотой изменения внешней ЭДС, ω.

При постоянном омическом сопротивлении контура R можно получить максимальную амплитуду тока, если:

ωL = или ω = , (6.19)

тогда: I ₀ = ; tg φ = 0; φ = 0. (6.20)

Условие ω = означает, что частота изменения внешней ЭДС равна частоте собственных колебаний контура ω = ω ₀.

Равенство частоты изменения внешней ЭДС и частоты собственных колебаний контура называют условием электрического резонанса. При этом, амплитуда силы тока I ₀ в контуре достигает максимального значения. Графически зависимость амплитуды тока I ₀ от соотношения частот вынужденных колебаний ω и собственных колебаний ω ₀ имеет вид:

Таким образом, величина максимума амплитуды тока зависит от величины активного сопротивления контура R.

Колебательный контур часто характеризуют его добротностью – это величина, равная произведению 2π на отношение энергии колебательной системы в любой момент времени t к убыли этой энергии за промежуток времени, равный периоду колебаний T.

В случае слабого затухания колебаний, добротность контура равна:

Q = . (6.21)

Экспериментальная установка, используемая в данной работе показана ниже

Колебательный контур состоит из катушки индуктивности L, магазина емкости С, переменного сопротивления R и сопротивления R ₁, а так же звукового генератора ЗГ.

Не нашли, что искали? Воспользуйтесь поиском: