Основы расчета изгибаемых элементов

Для изгибаемых элементов (балок), у которых пролет превышает высоту поперечного сечения (в 5 и более раз) изменение деформаций по высоте

сечения происходит по линейному закону, напряжения распределяются только до предела текучести σ_T (рис.2.1).

Напряжения в точках, находящихся на расстоянии “y” от нейтральной оси, определяются по формуле σ = М y / I_x, где - изгибающий момент в рассматриваемом сечении балки; I_x - момент инерции сечения.

Максимальное напряжение возникает когда 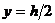: σ_max. = М(h/2)/I_x. Отношение момента инерции I_x к расстоянию от нейтральной оси до крайней

Точки сечения называется моментом сопротивления W_x = I_x(2/h), тогда σ_max = M/W_x..

Для проверки прочности изгибаемых элементов, работающих в пределах упругих деформаций, необходимо, чтобы максимальные нормальные и касательные напряжения в балке от расчетной нагрузки не превосходили соответствующих расчетных сопротивлений.

Рис.2.1. Изменение эпюры напряжений в изгибаемом элементе при развитии

пластических деформаций в материале

; (2.10)

τ = Q S /I t≤ R_{s 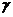c}.

где и - максимальный момент и поперечная сила в балке от расчетной нагрузки; - момент сопротивления нетто поперечного сечения балки, в случае несимметричного сечения балки выбирается W_nmin = I_x / y _max; - статический момент сдвигающейся части сечения относительно нейтральной оси; I - момент инерции сечения балки; 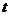- толщина стенки.

По второму предельному состоянию наибольший прогиб балки от нагрузки при эксплуатации сравнивается с предельной величиной указанной в нормах, либо в задании на проектирование.

Величина прогиба зависит от расчетной схемы балки, а предельный прогиб – от назначения. Например, для главной балки рабочей площадки промздания, имеющей один пролет и шарнирные опоры, загруженной равномерно распределенной нагрузкой, проверка прогиба производится по формуле:

5 q_n l⁴

f_max = --------------- ≤ l / 400, (2.11)

384 E I

где - максимальный прогиб балки; - нормативная нагрузка на балку; - прогиб балки; E I - изгибная жесткость балки; 400 – норма прогиба балки.

Формула для проверки прочности изгибаемых элементов при наличии пластических деформаций (пластический шарнир) получается из выражения (2.10) путем замены на , т.е.

M / (c W_n) ≤ R_y γ_c или M / W_n ≤ cR_y γ_c (2.12).

Сравнивая это выражение с (2.10) видим, что формально учет пластических деформаций сводится к повышению расчетного сопротивления умножением на величину “c”, коэффициент, характеризующий резерв несущей способности изгибаемого элемента, обусловленный пластической работой металла, и определенный по формуле для балок двутаврового сечения, как наиболее распространенного в изгибаемых элементах

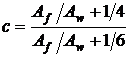, (2.13)

где - отношение площадей поперечного сечения пояса и стенки балки.

Для прокатных двутавров различных типов 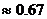, чему соответствует значение с = 1,1.

Для составных двутавров (рис.2.2, в). коэффициент “c” вычисляется по формуле (2.13).

Для прямоугольного сечения, когда площадь поясов балки можно приравнять к нулю – с = 1,5 (рис.2.2, б).

Устремляя площадь стенки к нулю (рис.2.2, е) из двутавра получаем расчетные сечения фермы или балки с гибкой стенкой, тогда с = 1.

Наибольшим пластическим резервом будет обладать балка с поперечным сечением (см. рис.2.2, а), для нее с = 2.

Практически выбор формы поперечного сечения изгибаемых элементов зависит от многих факторов, среди которых главным является расход металла, так как его стоимость составляет 80% общей стоимости конструкции.

Кроме нормальных напряжений σ в балках возникают и касательные напряжения τ_xy, зависящие от поперечной силы и локальных напряжений σ_y в местах передачи на балку сосредоточенных нагрузок. Например, для балок, загруженных сосредоточенными силами по пролету (рис.2.3, а) определяющей

будет компонента σ_x. При большей сосредоточенной нагрузке на балке с малым пролетом (рис.2.3, б) определяющим будет напряжение τ_xy.

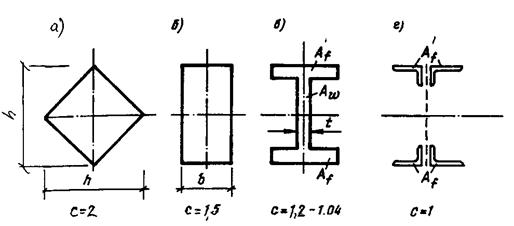
Рис.2.2. Зависимость коэффициента “c” от формы поперечного сечения

Не нашли, что искали? Воспользуйтесь поиском: