ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
СБОРНИК ЗАДАЧ ПО ОБЩЕЙ ФИЗИКЕ 1 страница
Вариант 2

• 5.2.1. На некотором расстоянии друг от друга в точках О и Внаходятся два одинаковых по модулю точечных заряда. На рисунке показано распределение напряженности электростатического поля между зарядами Е(г). Определите знаки зарядов.
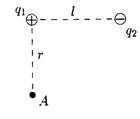
• 5.2.2. Отрицательный заряд q1=-5qи положительный q2 = +2qзакреплены на расстоянии r друг от друга. Где на линии, соединяющей заряды, следует поместить положительный заряд Q, чтобы он находился в равновесии.
• 5.2.3. Параллельно бесконечной плоскости, заряженной с поверхностной плотностью заряда σ= 4,0 мкКл/м2, расположена бесконечно длинная прямая нить, заряженная с линейной плотностью заряда τ = 100 нКл/м2. Определите силу F, действующую со стороны плоскости на отрезок нити, длиной L = 1,0 м.

• 5.2.4. На рисунке показано распределение напряженности электростатического поля Ех(х), созданного двумя параллельными заряженными бесконечными пластинами, вдоль направления х. Как различаются поверхностные плотности зарядов σ1 и σ2 на этих пластинах по знаку и по модулю?
• 5.2.5. Точечный заряд q= 1,0·10 6Кл помещен в центр куба с ребром а = 0,5 м. Чему равен поток вектора напряженности через каждую грань куба?
 • 5.2.6. По тонкому кольцу радиусом г = 8,0 см равномерно распределен заряд с линейной плотностью τ= 10 нКл/м. Используя принцип суперпозиции, определите напряженность электростатического поля Ев точке О, равноудаленной от всех точек кольца на расстояние l = 10 см.
• 5.2.6. По тонкому кольцу радиусом г = 8,0 см равномерно распределен заряд с линейной плотностью τ= 10 нКл/м. Используя принцип суперпозиции, определите напряженность электростатического поля Ев точке О, равноудаленной от всех точек кольца на расстояние l = 10 см.
 • 5.2.7. Бесконечная плоскость равномерно заряжена с поверхностной плотностью заряда +σ. Справа от плоскости и параллельно ей расположен бесконечно большой слой заряда толщиной d, равномерно заряженный с объемной плотностью заряда +ρ. Все заряды неподвижны. Используя теорему Гаусса и учитывая симметрию поля слоя заряда относительно плоскости mn, найдите напряженность поля Ена расстоянии d/2 от плоскости.
• 5.2.7. Бесконечная плоскость равномерно заряжена с поверхностной плотностью заряда +σ. Справа от плоскости и параллельно ей расположен бесконечно большой слой заряда толщиной d, равномерно заряженный с объемной плотностью заряда +ρ. Все заряды неподвижны. Используя теорему Гаусса и учитывая симметрию поля слоя заряда относительно плоскости mn, найдите напряженность поля Ена расстоянии d/2 от плоскости.
Вариант 3
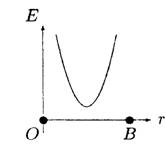 • 5.3.1. На некотором расстоянии друг от друга в точках О и Внаходятся два одинаковых по модулю точечных заряда. На рисунке показано распределение напряженности электростатического поля между зарядами Е(г).Определите знаки зарядов.
• 5.3.1. На некотором расстоянии друг от друга в точках О и Внаходятся два одинаковых по модулю точечных заряда. На рисунке показано распределение напряженности электростатического поля между зарядами Е(г).Определите знаки зарядов.
• 5.3.2. Расстояние между двумя точечными зарядами q1 = 7 · 10-9Кл и q2 = -14 · 10-9Кл равно 5,0 см. Найдите напряженность электростатического поля в точке, находящейся на расстоянии 3.0 см от положительного заряда и 4,0 см от отрицательного.
• 5.3.3. С какой силой, приходящейся на единицу площади, отталкиваются две одноименно заряженные бесконечно протяженные плоскости с одинаковой поверхностной плотностью заряда σ= - 2,0 мкКл/м2?
| о\ |
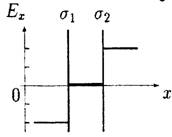 • 5.3.4. На рисунке показано распределение напряженности электростатического поля Ех(х), созданного двумя параллельными заряженными бесконечными пластинами, вдоль направления х. Как различаются поверхностные плотности зарядов σ1и σ2 на этих пластинах по знаку и по модулю?
• 5.3.4. На рисунке показано распределение напряженности электростатического поля Ех(х), созданного двумя параллельными заряженными бесконечными пластинами, вдоль направления х. Как различаются поверхностные плотности зарядов σ1и σ2 на этих пластинах по знаку и по модулю?
 • 5.3.5. Сравните входящий и выходящий потоки вектора напряженности Е однородного электростатического поля через замкнутую поверхность прямой трехгранной призмы. Передняя грань призмы перпендикулярна Е и имеет размеры h x h, а нижняя - параллельна Е.
• 5.3.5. Сравните входящий и выходящий потоки вектора напряженности Е однородного электростатического поля через замкнутую поверхность прямой трехгранной призмы. Передняя грань призмы перпендикулярна Е и имеет размеры h x h, а нижняя - параллельна Е.
5.3.6. По поверхности диска радиусом R = 1,0 см равномерно распределен заряд q= 1,0·10-9Кл. Используя принцип суперпозиции, найдите напряженность электростатического поля Е в точке, расположенной на перпендикуляре к диску на расстоянии h = 1.0 см от его центра.
• 5.3.7. Лист стекла толщиной d с диэлектрической проницаемостью е равномерно заряжен с объемной плотностью заряда +ρ. Используя теорему Гаусса и учитывая симметрию поля слоя относительно плоскости MN, определите напряженность Е и электрическое смещение D в точках А, В, С. Постройте графики зависимости Е(х) и D(x), где х – расстояние от точки О.

 5.4. Вариант 4
5.4. Вариант 4
• 5.4.1. На некотором расстоянии друг от друга в точках О к Внаходятся два одинаковых по модулю точечных заряда. На рисунке показано распределение напряженности электростатического поля Е(r) между зарядами. Определите знаки зарядов.
• 5.4.2. В вершинах квадрата со стороной а находятся одинаковые заряды +q. Какой заряд Q необходимо поместить в центре квадрата, чтобы вся система зарядов находилась в равновесии?
 • 5.4.3. Бесконечная прямая нить, равномерно заряженная с линейной плотностью заряда τ1=+3,0·10-7Кл/м2, и отрезок нити длиной l = 20 см, равномерно заряженный с линейной плотностью заряда τ=+2,0·10-7Кл/м2. расположены в одной плоскости перпендикулярно друг другу на расстоянии rо = 10 см. Определите силу взаимодействия между ними.
• 5.4.3. Бесконечная прямая нить, равномерно заряженная с линейной плотностью заряда τ1=+3,0·10-7Кл/м2, и отрезок нити длиной l = 20 см, равномерно заряженный с линейной плотностью заряда τ=+2,0·10-7Кл/м2. расположены в одной плоскости перпендикулярно друг другу на расстоянии rо = 10 см. Определите силу взаимодействия между ними.
 • 5.4.4 На рисунке показано распределение напряженности электростатического поля Еr(х), созданного двумя параллельными заряженными х бесконечными пластинами, вдоль направления.г. Как различаются поверхностные плотности зарядов σ1 и σ2 на этих пластинах по знаку и по модулю?
• 5.4.4 На рисунке показано распределение напряженности электростатического поля Еr(х), созданного двумя параллельными заряженными х бесконечными пластинами, вдоль направления.г. Как различаются поверхностные плотности зарядов σ1 и σ2 на этих пластинах по знаку и по модулю?
|
|
• 5.4.7. По поверхности длинной металлической трубки радиусом R = 4,0-10ˉ2м равномерно распределен заряд. Напряженность электростатического поля Е на расстоянии а = 0,10 м от оси трубки равна 100 В/м. Используя теорему Гаусса, найдите линейную и поверхностную плотность заряда трубки. Постройте график зависимости Е{r), где r - расстояние от оси трубки.
Вариант 5
|
|
ника со стороной а = 0,2 м помешены заряды |q| = 2,0-10ˉ9Кл. Найдите напряженность электростатического поля в точке В. расположенной на середине стороны треугольника.
•
|
нить лежат в одной плоскости, параллельной заряженной плоскости.
|
•5.5.4. На рисунке показано распределение напряженности электростатического поля Ех(х), созданного двумя параллельными заряженными бесконечными пластинами, вдоль направления х. Как различаются поверхностные плотности зарядов σ1и σ2на этих пластинах по знаку и по модулю?
•  5.5.5. Прямоугольная плоская площадка со сторонами а = 3,0 см и
5.5.5. Прямоугольная плоская площадка со сторонами а = 3,0 см и
b = 2,0 см находится на расстоянии r = 1,0 м от точечного заряда
q = 10 мкКл. Площадка ориентирована так, что линии напряженности
составляют угол α = 30° с ее поверхностью. Найдите поток вектора
напряженности Е через эту площадку.
•  5.5.6. Заряд q = 10 нКл равномерно распределен по дуге окружности,
5.5.6. Заряд q = 10 нКл равномерно распределен по дуге окружности,
радиус которой R = 1,0 см. а угол раствора α= 2π/3.Используя принцип
суперпозиции, определите напряженность электростатического поля Е в центре кривизны дуги.
• 5.5.7. Металлическому шару сообщен заряд q=-3,3•10ˉ8Кл. Напряженность поля в точке, удаленной на расстояние α=10•10ˉ2м
от поверхности шара, равна 1,2 • 10ˉ5В/м. Используя теорему Гаусса,
определите радиус шара и построите график зависимости Е(r). где r -
расстояние от центра шара.
Вариант 6
|
|
|
• 5.6.4. На рисунке показано распределение напряженности электростатического поля Ех(х), созданного двумя параллельными заряженными х бесконечными пластинами, вдоль направления х. Как различаются поверхностные плотности зарядов σ1 и σ2на этих пластинах по знаку и по модулю?
• 5.6.5. Плоская квадратная рамка со стороной а = 10 см находится на некотором расстоянии от бесконечной равномерно заряженной плоскости с поверхностной плотностью заряда σ = +1,0 мкКл/м2. Поверхность рамки составляет угол β = 30° с линиями напряженности поля, созданного плоскостью. Найдите поток вектора электрического смещения Ф D через плоскость рамки.
|
|
Вариант 7
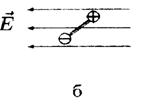
• 5.7.1. Как будет вести себя диполь в каждом из электростатических полей, изображенных на рисунках а, б, в?
|
|
|
• 5.7.2. Определите напряженность электростатического поля в центре
шестиугольника со стороной а, в вершинах которого расположены:
а) равные заряды одного знака; б) заряды равные по модулю, но чередующиеся по знаку.
•  5.7.3. Пластины плоского конденсатора площадью 1.0-10ˉ2м2 каждая
5.7.3. Пластины плоского конденсатора площадью 1.0-10ˉ2м2 каждая
притягиваются с силой 1,2. 10ˉ2Н. Пространство между пластинами
заполнено диэлектриком с ε = 2,0. Определите: а) модуль вектора электрического смещения |D|; б) заряд каждой пластины.
5.7.4. На рисунке показано распределение на-пряженности электростатического поля Ех(х), созданного двумя параллельными заряженными бесконечными пластинами, вдоль направления х. Как различаются поверхностные плотности зарядов σ1и σ2 на этих пластинах по знаку и по
модулю?
•
|
поверхности; б) внутри незамкнутой поверхности. Площади поверхностей равны.
•
|
мерно заряженные с линейной плотностью заряда г = 2,0•10ˉ12Кл тонкие нити длиной l =1,0 м. Точка А находится, в одной плоскости с нитями и удалена от концов нитей на расстояния 2а и а, как показано на рисунке (a = 0,40 м).
|
|
ее удален на расстояние а от центра шара. Для нахождения поля используйте теорему Гаусса.
5.8. Вариант 8
5.8.1. Как будет вести себя незаряженный шар в каждом из электростатических полей, изображенных на рисунках а, б, в?
|
• 5.8.2. Два равных по величине заряда |q1| = |q2| = 3,0·10ˉ9 Кл рас
положены в вершинах острых углов равнобедренного прямоугольного
треугольника на расстоянии l = 2,0 см. Определите, с какой силой оба
заряда действуют на третий заряд q3 = +1,0·10ˉ9 Кл, находящийся в
вершине прямого угла треугольника. Рассмотрите случаи, когда пер
вые два заряда: а) одноименные; б) разноименные. Ответ поясните рисунками.
• 5.8.3. Три тонкие металлические пластины, расположенные параллельно друг другу, имеют заряды q, 2 q и - 3q. Расстояние между пластинами равно d, площадь каждой S. Определите силу, действующую на среднюю пластину, если d много меньше линейных размеров пластин.
|
• 5.8.5. В центре сферы радиусом R = 20 см находится точечный за
ряд Q = 10 нКл. Определите поток вектора напряженности электростатического поля Фе через часть сферической поверхности площадью
S = 20 см2.
• 5.8.6. На тонкой пластинке, имеющей форму кольца с внутренним радиусом r и внешним R, равномерно распределен заряд q. Используя
принцип суперпозиции, найдите зависимость напряженности электростатического поля Е(х) вдоль оси кольца, где х - расстояние от центра
кольца. Постройте график зависимости Е(х). Анализируя зависимость
Е(х), получите выражение для напряженности поля в случаях, когда
а) r = 0 (диск); б) r ≈ R (кольцо).
• 5.8.7. Две длинные тонкостенные коаксиальные трубки радиусами R1 =
2,0 см и R2 = 4,0см равномерно заряжены с линейными плотностями зарядов соответственно r1 = +1,0 нКл/м и r2 = -0,5 нКл/м. В пространстве между трубками - воздух. Определите напряженность электростатического поля в точках, находящихся на расстояниях 1,0 см, 3,0 см и 5,0 см от оси. Постройте график зависимости Ег(r),где r - расстояние от оси трубок.
Вариант 9
• 5.9.1. Между точечным зарядом +Q и бесконечной пластиной, равномерно заряженной с поверхностной плотностью заряда - σ, находится диполь. В каком направлении он будет двигаться?
• 5.9.2. Три одинаковых положительных заряда величиной q каждый рас
положены в вершинах равностороннего треугольника со стороной а.
Какой отрицательный заряд Q надо поместить в центре треугольника,
чтобы система из четырех зарядов находилась в равновесии?
• 5.9.3. Электростатическое поле образовано положительно заряженной
бесконечно длинной нитью. Протон, двигаясь под действием этого поля
от точки, находящейся на расстоянии х1 = 1,0 см от нити, до точки
x 2= 4,0 см, изменил свою скорость от 2,0-105 до 3,0·106м/с. Найдите
линейную плотность заряда нити т. Масса протона m = 6,67·10ˉ27кг.
|
созданного двумя параллельными заряженными
бесконечными пластинами, вдоль направления х.
Как различаются поверхностные плотности за
рядов σ1 и σ2 на этих пластинах по знаку и по
модулю?
|
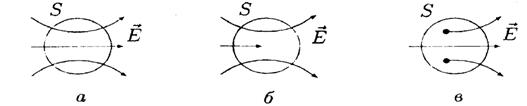
через замкнутые поверхности S. сечения которых показаны на рисунках а,б,в
|
 • 5.9.6. По дуге, длина которой равна ⅔ длины окружности радиусом R = 10 см, равномерно распределен заряд с линейной плотностью г = 0,2 мкКл/м. Используя принцип суперпозиции, определите напряженность электростатического поля Е в центре кривизны дуги.
• 5.9.6. По дуге, длина которой равна ⅔ длины окружности радиусом R = 10 см, равномерно распределен заряд с линейной плотностью г = 0,2 мкКл/м. Используя принцип суперпозиции, определите напряженность электростатического поля Е в центре кривизны дуги.
•
|
•5.10. Вариант 10
•5.10.1. На рисунках а,) б), в) показаны линии напряженности электростатических полей. Сравните величины напряженности в точках 1, 2, 3.
•
|
|
• 5.10.4. На рисунке показано распределение напряженности электростатического поля Ех(х),
созданного двумя параллельными заряженными
бесконечными пластинами, вдоль направления х.
Как различаются поверхностные плотности за
рядов σ1 и σ2 на этих пластинах по знаку и по
модулю?
5.10.5. Равномерно заряженную плоскость с поверхностной плотностью заряда а = +10 нКл/м2 пересекает сфера, центр которой лежит на плоскости. Поток вектора напряженности поля Е через сферу Ф E = 3,2 Вм. Определите радиус сферы.
|
|
5.11. Вариант 11
•
|
|
• 5.11.2. В вершинах шестиугольника со стороной а = 10 см расположены
точечные заряды q, 2q, 3q, 4q, 5q, 6q (q= 0,10 мкКл). Найдите силу,
действующую на точечный заряд q, лежащий в плоскости шестиугольника и равноудаленный от его вершин.
• 5.11.3. Два взаимно перпендикулярных бесконечных провода, равно
мерно заряженных с линейными плотностями заряда r1и r2, находятся
на расстоянии а друг от друга. Как зависит сила взаимодействия
проводников от расстояния между ними?
|
• 5.11.5. Бесконечно длинный цилиндр радиусом R = 0,10 м равномерно
заряжен с поверхностной плотностью заряда а = + 1,0 • 10-10Кл/м2.
Определите поток вектора напряженности Е через коаксиальную цилиндрическую поверхность единичной длины, если радиус этой цилиндрической поверхности: а) r < R; б) r > R.
Не нашли, что искали? Воспользуйтесь поиском: