Теоретическое введение. Эффект Холла состоит в появлении в проводнике с током, помещенном в магнитное поле, электрического поля в направлении

Эффект Холла состоит в появлении в проводнике с током, помещенном в магнитное поле, электрического поля в направлении, перпендикулярном току и магнитной индукции. Эффект был открыт американским физиком Холлом в 1879 году. Он наблюдается во всех металлах и полупроводниках независимо от их материала, однако в последних он выражен сильнее.

В настоящее время эффект Холла является одним из наиболее эффективных методов исследования носителей тока, особенно в полупроводниках. Он позволяет оценить концентрацию носителей (электронов и “дырок”), определить их подвижность и знак, что в свою очередь, позволяет судить о количестве примесей в полупроводниках и характере химической связи.

Явление Холла широко используется в технике для контроля качества металлов и полупроводников, а также в измерительной и вычислительной технике, автоматике и радиоэлектронике.

Поместим теперь образец в магнитное поле, направленное по оси y (рис.1). Тогда на свободные носители зарядов (для определенности - электроны), движущиеся со скоростью 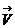, в направлении противоположном оси х, будет действовать сила Лоренца _л

, (1)

где е - заряд электрона (е < 0);

- средняя скорость упорядоченного движения носителей зарядов;

- индукция магнитного поля.

В нашем случае эта сила действует вдоль оси z (см.рис.1б) и равна (т.к. ^ ):

Здесь под V_x имеется в виду средняя (дрейфовая) скорость носителей зарядов вдоль оси x, возникающая при наложении внешнего электрического поля напряженностью Е_x.

Под действием силы Лоренца электроны отклоняются к верхней грани, заряжая ее отрицательно. На нижней грани накаливаются нескомпенсированные положительные заряды. Это приводит к возникновению дополнительного поперечного электрического поля 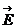_z, направленного от нижней грани к верхней, и к появлению разности потенциалов Dj между гранями.

Dj = Е_z d (3)

Когда напряженность поля 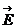_z достигнет такой величины, что электрическая сила _е, действующая на электроны, будет уравновешена силой _л, установится стационарное распределение зарядов в поперечном направлении. Поле 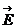_z складывается с полем 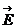_x в результирующее поле 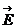. Так как потенциальные поверхности всегда перпендикулярны в каждой точке к вектору 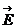, следовательно, они займут положения, изображенные на рис.2.

Точки 1 и 2, которые прежде лежали на одной и той же эквипотенциальной поверхности, теперь будут иметь разные потенциалы, т.е. появится поперечная разность потенциалов, которая и характеризует эффект Холла.

Направление холловской разности потенциалов зависит от знака носителей тока. В полупроводниках ток может создаваться движением как отрицательных зарядов - электронов, так и положительных - дырок.

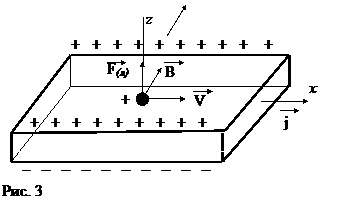В случае электронной проводимости, электроны отклоняясь под действием силы Лоренца, будут заряжать верхнюю грань пластины отрицательно по отношению к нижней, и, наоборот, в случае дырочной проводимости верхняя грань будет заряжаться положительно по отношению к нижней(см.рис.3).

Получим выражение для холловской разности потенциалов.

В установившемся состоянии сила, действующая на заряд со стороны поперечного электрического поля

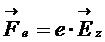(4)

уравновешивает силу Лоренца, так что

(5)

Дальнейшее накопление электрических зарядов на гранях пластины прекращается. Переходя от векторного уравнения (5) к уравнению в проекциях на ось z с учетом (2) получаем:

е v _x В = е Е_z (6)

откуда

Е_z = v _xВ (7)

После подстановки (7) в (3) находим

Dj = v _x В d (8)

Модуль плотность тока j может быть найден из выражения

j = е n v _x, (9)

где n - концентрация носителей зарядов и связанна с током в рассматриваемом случае соотношением:

I = j S = j a d = e n v _x а d, (10)

где S - площадь поперечного сечения образца, S = а d

Выражая v _x из (10) и подставляя в (8), находим

(11)

Если учесть статистический характер распределения скоростей носителей зарядов, то в выражение (11) войдет множитель " К ", зависящий от температуры образца. Для температур, при которых производятся наши измерения

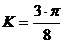(12)

Итак окончательно получаем:

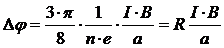, (13)

где величина

(14)

называетсяпостоянной Холла и зависит от природы вещества.

Знак поперечной разности потенциалов Dj зависит от знака носителей тока. Для электронного полупроводника R < 0, а для дырочного R > 0.

Таким образом, по знаку постоянной Холла можно определить знак носителей тока. Если в полупроводнике осуществляются оба типа проводимости, по знаку константы Холла можно судить о том, какая из них является преобладающей.

С помощью постоянной Холла можно определить концентрацию носителей тока, если характер проводимости и заряд носителей известен.

(15)

Зная постоянную Холла и удельное сопротивление полупроводника r, можно определить также подвижность носителей тока b (отношение скорости направленного движения носителей заряда, вызванного электрическим полем, к напряженности этого поля).

Действительно, модуль скорости дрейфа v _x носителей тока в электрическом поле определяется его напряженностью

v _x = b Е_x (16)

Напряженность поля Е_x определяется из закона Ома в дифференциальной форме

j = s Е_x,

E_x=r j, (17)

где s и r - проводимость и удельное сопротивление полупроводника, соответственно.

Используя соотношение (9), (14), (16-17), легко получить следующее выражение для расчета подвижности носителей тока

b= (18)

Не нашли, что искали? Воспользуйтесь поиском: