ЭЛЕКТРИЧЕСТВО И ЭЛЕКТРОМАГНЕТИЗМ 8 страница

Поток Y создается током I ₁, поэтому, согласно (128.1), получаем

(128.3)

Если вычислить магнитный поток, создаваемый катушкой 2 сквозь катушку 1, то для L ₁₂ получим выражение в соответствии с формулой (128.3). Таким образом, взаимная индуктивность двух катушек, намотанных на общий тороидальный сердечник,

§ 129. Трансформаторы

Принцип действия трансформаторов, применяемых для повышения или понижения напряжения переменного тока, основан на явлении взаимной индукции. Впервые трансформаторы были сконструированы и введены в практику русским электротехни­ком П.Н. Яблочковым (1847—1894) и русским физиком И.Ф. Усагиным (1855—1919). Принципиальная схема трансформатора показана на рис. 186. Первичная и вторичная катушки (обмотки), имеющие соответственно N ₁ и N ₂ витков, укреплены на замкнутом железном сердечнике. Так как концы первичной обмотки присоединены к источнику переменного напряжения с э.д.с. 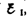, то в ней возникает переменный ток I ₁, создающий в сердечнике трансформатора переменный магнитный поток Ф, который практически полностью локализован в железном сердечнике и, следовательно, почти целиком пронизывает витки вторичной обмотки. Изменение этого потока вызывает во вторич­ной обмотке появление э.д.с. взаимной индукции, а в первичной — э.д.с. самоиндукции.

Ток I ₁ первичной обмотки определяется согласно закону Ома:

(129.1)

где R ₁ — сопротивление первичной обмотки. Падение напряжения I ₁ R ₁ на сопротивле­нии R ₁ при быстропеременных полях мало2 по сравнению с каждой из двух э.д.с., поэтому

(129.2)

Э.д.с. взаимной индукции, возникающая во вторичной обмотке,

(129.3)

Сравнивая выражения (129.1) и (129.2), получим, что э.д.с., возникающая во вторичной обмотке,

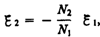
где знак минус показывает, что э.д.с. в первичной и вторичной обмотках проти­воположны по фазе.

Отношение числа витков N ₂ /N ₁, показывающее, во сколько раз э.д.с. во вторичной обмотке трансформатора больше (или меньше), чем в первичной, называется коэффициентом трансформации.

Пренебрегая потерями энергии, которые в современных трансформаторах не пре­вышают 2% и связаны в основном с выделением в обмотках джоулевой теплоты и появлением вихревых токов, и применяя закон сохранения энергии, можем записать, что мощности тока в обеих обмотках трансформатора практически одинаковы:

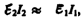
откуда, учитывая соотношение (129.3), найдем

т. е. токи в обмотках обратно пропорциональны числу витков в этих обмотках.

Если N ₂ /N ₁>1, тоимеем дело с повышающим трансформатором, увеличивающим переменную э.д.с. и понижающим ток (применяются, например, для передачи электро­энергии на большие расстояния, так как в данном случае потери на джоулеву теплоту, пропорциональные квадрату силы тока, снижаются); если N ₂ /N ₁ < 1, то имеем дело с понижающим трансформатором, уменьшающим э.д.с. и повышающим ток (применя­ются, например, при электросварке, так как для нее требуется большой ток при низком напряжении).

Мы рассматривали трансформаторы, имеющие только две обмотки. Однако транс­форматоры, используемые в радиоустройствах, имеют 4—5 обмоток, обладающих разными рабочими напряжениями. Трансформатор, состоящий из одной обмотки, называется автотрансформатором. В случае повышающего автотрансформатора э.д.с. подводится к части обмотки, а вторичная э.д.с. снимается со всей обмотки. В понижа­ющем автотрансформаторе напряжение сети подается на всю обмотку, а вторичная э.д.с. снимается с части обмотки.

§ 130. Энергия магнитного поля

Проводник, по которому протекает электрический ток, всегда окружен магнитным полем, причем магнитное поле появляется и исчезает вместе с появлением и исчезнове­нием тока. Магнитное поле, подобно электрическому, является носителем энергии. Естественно предположить, что энергия магнитного поля равна работе, которая затра­чивается током на создание этого поля.

Рассмотрим контур индуктивностью L, по которому течет ток I. С данным кон­туром сцеплен магнитный поток (см. (126.1)) Ф =LI, причем при изменении тока на d I магнитный поток изменяется на dФ= L d I. Однако для изменения магнитного потока на величину dФ (см. § 121) необходимо совершить работу d А=I dФ =LI d I. Тогда работа по созданию магнитного потока Ф будет равна

Следовательно, энергия магнитного поля, связанного с контуром,

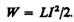(130.1)

Исследование свойств переменных магнитных полей, в частности распространения электромагнитных волн, явилось доказательством того, что энергия магнитного поля локализована в пространстве. Это соответствует представлениям теории поля.

Энергию магнитного поля можно представить как функцию величин, характеризу­ющих это поле в окружающем пространстве. Для этого рассмотрим частный слу­чай — однородное магнитное поле внутри длинного соленоида. Подставив в формулу (130.1) выражение (126.2), получим

Так как I=Bl/ (m ₀ mN) (см. (119.2)) и В=m ₀ mH (см. (109.3)), то

(130.2)

где Sl = V — объем соленоида.

Магнитное поле соленоида однородно и сосредоточено внутри него, поэтому энергия (см. (130.2)) заключена в объеме соленоида и распределена в нем с постоянной объемной плотностью

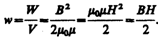(130.3)

Выражение (130.3) для объемной плотности энергии магнитного поля имеет вид, аналогичный формуле (95.8) для объемной плотности энергии электростатического поля, с той разницей, что электрические величины заменены в нем магнитными. Формула (130.3) выведена для однородного поля, но она справедлива и для неоднород­ных полей. Выражение (130.3) справедливо только для сред, для которых зависимость В от Н линейная, т.е. оно относится только к пара- и диамагнетикам (см. § 132).

Задачи

Глава 16 Магнитные свойства вещества

§ 131. Магнитные моменты электронов и атомов

Рассматривая действие магнитного поля на проводники с током и на движущиеся заряды, мы не интересовались процессами, происходящими в веществе. Свойства среды учитывались формально с помощью магнитной проницаемости m. Для того чтобы разобраться в магнитных свойствах сред и их влиянии на магнитную индукцию, необходимо рассмотреть действие магнитного поля на атомы и молекулы вещества.

Опыт показывает, что все вещества, помещенные в магнитное поле, намагничива­ются. Рассмотрим причину этого явления с точки зрения строения атомов и молекул, положив в основу гипотезу Ампера (см. § 109), согласно которой в любом теле существуют микроскопические токи, обусловленные движением электронов в атомах и молекулах.

Для качественного объяснения магнитных явлений с достаточным приближением можно считать, что электрон движется в атоме по круговым орбитам. Электрон, движущийся по одной из таких орбит, эквивалентен круговому току, поэтому он обладает орбитальным магнитным моментом (см. (109.2)) p _m= IS n, модуль которого

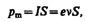(131.1)

где I=en — сила тока, n — частота вращения электрона по орбите, S — площадь орбиты. Если электрон движется по часовой стрелке (рис. 187), то ток направлен против часовой стрелки и вектор р _m (в соответствии с правилом правого винта) направлен перпендикулярно плоскости орбиты электрона, как указано на рисунке.

С другой стороны, движущийся по орбите электрон обладает механическим момен­том импульса L _e, модуль которого, согласно (19.1),

(131.2)

где v = 2 pn, pr ² = S. Вектор L _e (его направление также определяется по правилу правого винта) называется орбитальным механическим моментом электрона.

Из рис. 187 следует, что направления р _m и L _e, противоположны, поэтому, учитывая выражения (131.1) и (131.2), получим

(131.3)

где величина

(131.4)

называется гиромагнитным отношением орбитальных моментов (общепринято писать со знаком «–», указывающим на то, что направления моментов противоположны). Это отношение, определяемое универсальными постоянными, одинаково для любой ор­биты, хотя для разных орбит значения v и r различны. Формула (131.4) выведена для круговой орбиты, но она справедлива и для эллиптических орбит.

Экспериментальное определение гиромагнитного отношения проведено в опытах Эйнштейна и де Гааза* (1915), которые наблюдали поворот свободно подвешенного на тончайшей кварцевой нити железного стержня при его намагничении во внешнем магнитном поле (по обмотке соленоида пропускался переменный ток с частотой, равной частоте крутильных колебаний стержня). При исследовании вынужденных крутильных колебаний стержня определялось гиромагнитное отношение, которое ока­залось равным – (e/m). Таким образом, знак носителей, обусловливающих молекуляр­ные токи, совпадал со знаком заряда электрона, а гиромагнитное отношение оказалось в два раза бо2льшим, чем введенная ранее величина g (см. (131.4)). Для объяснения этого результата, имевшего большое значение для дальнейшего развития физики, было предположено, а впоследствии доказано, что кроме орбитальных моментов (см. (131.1) и (131.2)) электрон обладает собственным механическим моментом импульса L _es, называ­емым спином. Считалось, что спин обусловлен вращением электрона вокруг своей оси, что привело к целому ряду противоречий. В настоящее время установлено, что спин является неотъемлемым свойством электрона, подобно его заряду и массе. Спину электрона L _es, соответствует собственный (сотовый) магнитный момент р _ms, пропорци­ональный L _es и направленный в противоположную сторону:

(131.5)

*В. И. де Гааз (1878—1960) — нидерландский физик.

Величина g_s называется гиромагнитным отношением спиновых моментов.

Проекция собственного магнитного момента на направление вектора В может принимать только одно из следующих двух значений:

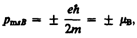
где ħ=h/ (2p) (h— постоянная Планка), m _b— магнетон Бора, являющийся единицей магнитного момента электрона.

В общем случае магнитный момент электрона складывается из орбитального и спинового магнитных моментов. Магнитный момент атома, следовательно, складывается из магнитных моментов входящих в его состав электронов и магнитного момента ядра (обусловлен магнитными моментами входящих в ядро протонов и ней­тронов). Однако магнитные моменты ядер в тысячи раз меньше магнитных моментов электронов, поэтому ими пренебрегают. Таким образом, общий магнитный момент атома (молекулы) p _a равен векторной сумме магнитных моментов (орбитальных и спиновых) входящих в атом (молекулу) электронов:

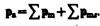(131.6)

Еще раз обратим внимание на то, что при рассмотрении магнитных моментов электронов и атомов мы пользовались классической теорией, не учитывая ограничений, накладываемых на движение электронов законами квантовой механики. Однако это не противоречит полученным результатам, так как для дальнейшего объяснения намаг­ничивания веществ существенно лишь то, что атомы обладают магнитными момен­тами.

§ 132. Диа- и парамагнетизм

Всякое вещество является магнетиком, т. е. оно способно под действием магнитного поля приобретать магнитный момент (намагничиваться). Для понимания механизма этого явления необходимо рассмотреть действие магнитного поля на движущиеся в атоме электроны.

Ради простоты предположим, что электрон в атоме движется по круговой орбите. Если орбита электрона ориентирована относительно вектора В произвольным об­разом, составляя с ним угол a (рис. 188), то можно доказать, что она приходит в такое движение вокруг В, при котором вектор магнитного момента р _m, сохраняя постоянным угол a, вращается вокруг вектора В с некоторой угловой скоростью. Такое движение в механике называется прецессией. Прецессию вокруг вертикальной оси, проходящей через точку опоры, совершает, например, диск волчка при замедлении движения.

Таким образом, электронные орбиты атома под действием внешнего магнитного поля совершают прецессионное движение, которое эквивалентно круговому току. Так как этот микроток индуцирован внешним магнитным полем, то, согласно правилу Ленца, у атома появляется составляющая магнитного поля, направленная проти­воположно внешнему полю. Наведенные составляющие магнитных полей атомов (молекул) складываются и образуют собственное магнитное поле вещества, ослабляющее внешнее магнитное поле. Этот эффект получил название диамагнитного эффекта, а вещества, намагничивающиеся во внешнем магнитном поле против направления поля, называются диамагнетиками.

В отсутствие внешнего магнитного поля диамагнетик немагнитен, поскольку в дан­ном случае магнитные моменты электронов взаимно компенсируются, и суммарный магнитный момент атома (он равен векторной сумме магнитных моментов (орбиталь­ных и спиновых) составляющих атом электронов) равен нулю. К диамагнетикам относятся многие металлы (например, Bi, Ag, Au, Сu), большинство органических соединений, смолы, углерод и т. д.

Так как диамагнитный эффект обусловлен действием внешнего магнитного поля на электроны атомов вещества, то диамагнетизм свойствен всем веществам. Однако наряду с диамагнитными веществами существуют и парамагнитные — вещества, нама­гничивающиеся во внешнем магнитном поле по направлению поля.

У парамагнитных веществ при отсутствии внешнего магнитного поля магнитные моменты электронов не компенсируют друг друга, и атомы (молекулы) парамаг­нетиков всегда обладают магнитным моментом. Однако вследствие теплового движе­ния молекул их магнитные моменты ориентированы беспорядочно, поэтому парамаг­нитные вещества магнитными свойствами не обладают. При внесении парамагнетика во внешнее магнитное поле устанавливается преимущественная ориентация магнитных моментов атомов по полю (полной ориентации препятствует тепловое движение атомов). Таким образом, парамагнетик намагничивается, создавая собственное маг­нитное поле, совпадающее по направлению с внешним полем и усиливающее его. Этот эффект называется парамагнитным. При ослаблении внешнего магнитного поля да нуля ориентация магнитных моментов вследствие теплового движения нарушается и парамагнетик размагничивается. К парамагнетикам относятся редкоземельные эле­менты, Pt, Аl и т.д. Диамагнитный эффект наблюдается и в парамагнетиках, но он значительно слабее парамагнитного и поэтому остается незаметным.

Из рассмотрения явления парамагнетизма следует, что его объяснение совпадает с объяснением ориентационной (дипольной) поляризации диэлектриков с полярными молекулами (см. § 87), только электрический момент атомов в случае поляризации надо заменить магнитным моментом атомов в случае намагничения.

Подводя итог качественному рассмотрению диа- и парамагнетизма, еще раз от­метим, что атомы всех веществ являются носителями диамагнитных свойств. Если магнитный момент атомов велик, то парамагнитные свойства преобладают над диама­гнитными и вещество является парамагнетиком; если магнитный момент атомов мал, то преобладают диамагнитные свойства и вещество является диамагнетиком.

§ 133. Намагниченность. Магнитное поле в веществе

Подобно тому, как для количественного описания поляризации диэлектриков вводи­лась поляризованность (см. § 88), для количественного описания намагничения магнетиков вводят векторную величину — намагниченность, определяемую магнитным моментом единицы объема магнетика:

где — магнитный момент магнетика, представляющий собой векторную сумму магнитных моментов отдельных молекул (см. (131.6)).

Рассматривая характеристики магнитного поля (см. § 109), мы вводили вектор магнитной индукции В, характеризующий результирующее магнитное поле, создава­емое всеми макро- и микротоками, и вектор напряженности Н, характеризующий магнитное поле макротоков. Следовательно, магнитное поле в веществе складывается из двух полей: внешнего поля, создаваемого током, и поля, создаваемого намагничен­ным веществом. Тогда можем записать, что вектор магнитной индукции результирующего магнитного ноля в магнетике равен векторной сумме магнитных индукций внешнего поля В ₀ (поля, создаваемого намагничивающим током в вакууме) и поля микротоков В ' (поля, создаваемого молекулярными токами):

(133.1)

где В ₀= m ₀ Н (см. (109.3)).

Для описания поля, создаваемого молекулярными токами, рассмотрим магнетик в виде кругового цилиндра сечения S и длины l, внесенного в однородное внешнее магнитное поде с индукцией В ₀. Возникающее в магнетике магнитное поле молекуляр­ных токов будет направлено противоположно внешнему полю для диамагнетиков и совпадать с ним по направлению для парамагнетиков. Плоскости всех молекулярных токов расположатся перпендикулярно вектору В ₀, так как векторы их магнитных моментов p _m антипараллельны вектору В ₀ (для диамагнетиков) и параллельны В ₀ (для парамагнетиков). Если рассмотреть любое сечение цилиндра, перпендикулярное его оси, то во внутренних участках сечения магнетика молекулярные токи соседних атомов направлены навстречу друг другу и взаимно компенсируются (рис. 189). Нескомпенсированными будут лишь молекулярные токи, выходящие на боковую поверхность цилиндра.

Ток, текущий по боковой поверхности цилиндра, подобен току в соленоиде и созда­ет внутри него поле, магнитную индукцию В' которого можно вычислить, учитывая формулу (119.2) для N = 1 (соленоид из одного витка):

(133.2)

где I' — сила молекулярного тока, l — длина рассматриваемого цилиндра, а магнит­ная проницаемость m принята равной единице.

С другой стороны, I'/l — ток, приходящийся на единицу длины цилиндра, или его линейная плотность, поэтому магнитный момент этого тока p = I'lS/l = I'V/l, где V — объем магнетика. Если Р — магнитный момент магнетика объемом V, то намаг­ниченность магнетика

(133.3)

Сопоставляя (133.2) и (133.3), получим, что

или в векторной форме

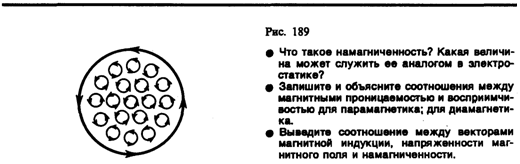
Подставив выражения для В ₀ и В' в (133.1), получим

(133.4)

или

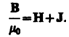(133.5)

Как показывает опыт, в несильных полях намагниченность прямо пропорциональ­на напряженности поля, вызывающего намагничение, т. е.

(133.6)

где c — безразмерная величина, называемая магнитной восприимчивостью вещества. Для диамагнстихов c отрицательна (поле молекулярных токов противоположно вне­шнему), для парамагнетиков — положительна (поле молекулярных токов совпадает с внешним).

Используя формулу (133.6), выражение (133.4) можно записать в виде

(133.7)

откуда

Безразмерная величина

(133.8)

представляет собой магнитную проницаемость вещества. Подставив (133.8) в (133.7), придем к соотношению (109.3) В = m ₀ m Н, которое ранее постулировалось.

Так как абсолютное значение магнитной восприимчивости для диа- и парамаг­нетиков очень мало (порядка 10^–4 —10^–6), то для них m незначительно отличается от единицы. Это просто понять, так как магнитное поле молекулярных токов значительно слабее намагничивающего поля. Таким образом, для диамагнетиков c<0 и m <1, для парамагнетиков c>0 и m >1.

Закон полного тока для магнитного поля в веществе (теорема о циркуляции вектора В) является обобщением закона (118.1):

где I и I' — соответственно алгебраические суммы макротоков (токов проводимости) и микротоков (молекулярных токов), охватываемых произвольным замкнутым кон­туром L. Таким образом, циркуляция вектора магнитной индукции В по произволь­ному замкнутому контуру равна алгебраической сумме токов проводимости и молеку­лярных токов, охватываемых этим контуром, умноженной на магнитную постоянную. Вектор В, таким образом, характеризует результирующее поле, созданное как мак­роскопическими токами в проводниках (токами проводимости), так и микроскопичес­кими токами в магнетиках, поэтому линии вектора магнитной индукции В не имеют источников и являются замкнутыми.

Из теории известно, что циркуляция намагниченности J по произвольному замкну­тому контуру L равна алгебраической сумме молекулярных токов, охватываемых этим контуром:

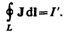
Тогда закон полного тока для магнитного поля в веществе можно записать также в виде

(133.9)

где I, подчеркнем это еще раз, есть алгебраическая сумма токов проводимости.

Выражение, стоящее в скобках в (133.9), согласно (133.5), есть не что иное, как введенный ранее вектор H напряженности магнитного поля. Итак, циркуляция вектора Н по произвольному замкнутому контуру L равна алгебраической сумме токов проводимости, охватываемых этим контуром:

(133.10)

Выражение (133.10) представляет собой теорему о циркуляции вектора Н.

§ 134. Условия на границе раздела двух магнетиков

Установим связь для векторов В и Н на границе раздела двух однородных магнетиков (магнитные проницаемости m ₁ и m ₂) при отсутствии на границе тока проводимости.

Построим вблизи границы раздела магнетиков 1 и 2 прямой цилиндр ничтожно малой высоты, одно основание которого находится в первом магнетике, другое — во втором (рис. 190). Основания D S настолько малы, что в пределах каждого из них вектор В одинаков. Согласно теореме Гаусса (120.3),

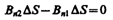
(нормали n и n' к основаниям цилиндра направлены противоположно). Поэтому

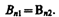(134.1)

Заменив, согласно B = m ₀ m H, проекции вектора В проекциями вектора Н, умножен­ными на m ₀ m, получим

(134.2)

Вблизи границы раздела двух магнетиков 1 и 2 построим небольшой замкнутый прямоугольный контур ABCDA длиной l, ориентировав его так, как показано на рис.191. Согласно теореме (133.10) о циркуляции вектора Н,

(токов проводимости на границе раздела нет), откуда

(знаки интегралов по AВ и CD разные, так как пути интегрирования противоположны, а интегралы по участкам BC и DA ничтожно малы). Поэтому

(134.3)

Заменив, согласно В = m ₀ m H, проекции вектора Н проекциями вектора В, деленными на m ₀ m, получим

(134.4)

Таким образом, при переходе через границу раздела двух магнетиков нормальная составляющая вектора В (В_n) и тангенциальная составляющая вектора Н (Н_t) изменя­ются непрерывно (не претерпевают скачка), а тангенциальная составляющая вектора В (B_t) и нормальная составляющая вектора Н (H_n) претерпевают скачок.

Из полученных условий (134.1)—(134.4) для составляющих векторов В и Н следует, что линии этих векторов испытывают излом (преломляются). Как и в случае диэлект­риков (см. § 90), можно найти закон преломления линий В (а значит, и линий Н):

(134.5)

Из этой формулы следует, что, входя в магнетик с большей магнитной проница­емостью, линии В и Н удаляются от нормали.

§ 135. Ферромагнетики и их свойства

Помимо рассмотренных двух классов веществ — диа- и парамагнетиков, называемых слабомагнитными веществами, существуют еще сильномагнитные вещества — ферромагнетики — вещества, обладающие спонтанной намагниченностью, т. е. они намагниче­ны даже при отсутствии внешнего магнитного поля. К ферромагнетикам кроме основ­ного их представителя — железа (от него и идет название «ферромагнетизм») — от­носятся, например, кобальт, никель, гадолиний, их сплавы и соединения.

Не нашли, что искали? Воспользуйтесь поиском: