
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Изучение магнитного поля соленоида. Цель работы: Определить индуктивность и индукцию магнитного поля соленоида в цепях постоянного и переменного тока.
Цель работы: Определить индуктивность и индукцию магнитного поля соленоида в цепях постоянного и переменного тока.
Оборудование: Дроссельная катушка (соленоид), амперметры постоянного и переменного тока, вольтметры постоянного и переменного тока, ключ, соединительные провода, источник питания постоянного и переменного напряжения (выпрямитель В-24), стальной сердечник.
I Теоретическое введение
Известно, что любой проводник с током создает вокруг себя магнитное поле, характеризуемое векторной величиной  - магнитной индукцией, которая пропорциональна силе тока I, т.е. В~I (закон Био-Савара-Лапласса). Следовательно, и магнитный поток Ф сквозь поверхность S, ограниченную замкнутым проводником (контуром), прямо пропорционален I: по определению Ф~ВS, а т.к. В~I, то Ф~I, или
- магнитной индукцией, которая пропорциональна силе тока I, т.е. В~I (закон Био-Савара-Лапласса). Следовательно, и магнитный поток Ф сквозь поверхность S, ограниченную замкнутым проводником (контуром), прямо пропорционален I: по определению Ф~ВS, а т.к. В~I, то Ф~I, или
Ф=L∙I (1)
Коэффициент пропорциональности L называется индуктивностью контура и равен:
 (2)
(2)
Если контур является катушкой из N витков, то магнитный поток усиливается в N раз и тогда
 (2)
(2)
где величина Ψ=N∙Ф называется потокосцеплением.
Согласно (2), индуктивность зависит от размеров и формы контура, а также от магнитных свойств окружающей среды. Так, приближение ферромагнетиков к соленоиду существенно увеличивает его индуктивность.
Если учесть, что магнитный поток сквозь каждый виток соленоида Ф=В∙S (здесь S – площадь одного витка), а магнитная индукция внутри длинного соленоида В=µ∙µ0∙I∙n; ( ), то полный магнитный поток, пронизывающий виток соленоида, равен:
), то полный магнитный поток, пронизывающий виток соленоида, равен:
Ψ=N∙Ф=µ∙µ0∙n²∙V∙I (3)
Здесь  - плотность витков, V=S∙l – объем.
- плотность витков, V=S∙l – объем.
Сопоставляя формулы (2) и (3), находим индуктивность длинного соленоида:
 (4)
(4)
Здесь µ - относительная магнитная проницаемость среды;
µ0 – магнитная постоянная.
Формула (4) является приближенной. Более точно индуктивность можно определить, основываясь на явлении самоиндукции.
Э. д. с. Самоиндукции, индуцированная в катушке, пропорциональна скорости изменения магнитного потока через витки катушки:
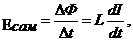 откуда
откуда 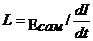 (5)
(5)
Единицей измерения индуктивности является I Гн (генри). Если в катушке при изменении тока на I A в течение I с возникает э.д.с. в I В, то индуктивность такой катушки равна I Гн.
В данной лабораторной работе для определения индуктивности соленоида используется способ, еще более точный. Эксперимент указывает на то, что сопротивление катушки индуктивности постоянному и переменному токам различно. Это свойство и используется для определения индуктивности катушки в данной работе.
При подключении катушки индуктивности к источнику постоянного тока, измеряя напряжение U на клеммах катушки и Сулу тока I в цепи, можно с помощью закона Ома определить сопротивление катушки постоянного тока:
 (6)
(6)
Такое сопротивление называется активным и зависит от материала, площади сечения и длины проволоки, из которой намотана катушка. При подключении катушки индуктивности к источнику переменного тока, напряжение на выходе которого изменяется по закону:
U=Umcos(Ωt+φ0)
сила тока в катушке тоже будет изменяться по гармоническому закону с той же циклической частотой Ω.
I=Im∙cos(Ωt-φ), 
Амплитуда силы тока в катушке связана с амплитудой Um законом Ома для переменного тока:

Здесь Z – полное сопротивление катушки индуктивности переменному току:
 (7)
(7)
Здесь R – активное сопротивление;
ХL=Ω∙L – индуктивное сопротивление.
Полное сопротивление катушки можно определить, измеряя не только амплитудные, но и действующие (эффективные) значений напряжения U˜ и сила тока I˜ в цепи, содержащей источник переменного напряжения и катушку:

 т.к. I˜=Im/√2, U˜=Um/√2 (8)
т.к. I˜=Im/√2, U˜=Um/√2 (8)
 |
С помощью формул (6), (7), (8) можно найти индуктивность катушки:
здесь ν – линейная частота гармонического колебания напряжения.
В нашем случае ν = 50Гц.
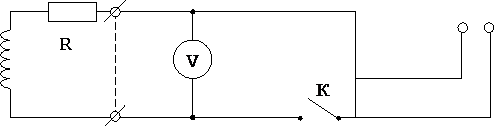
II. Схема установки

|
 ИП
ИП
 | ||||||||||
 |  | |||||||||
 | ||||||||||
 | ||||||||||
 | ||||||||||
Здесь R означает омическое(активное) сопротивление соленоида L. К – ключ, А и V – измерительный амперметр и вольтметр, ИП – источник постоянного и переменного тока (источник питания).
III. Выполнение работы
Ознакомиться с содержанием теоретического введения и схемой установки. Продумать ответ на контрольные вопросы.
Подготовить бланк отчета к работе: вписать в него необходимые формулы, определения, таблицу, схему и осмыслить ход проведения опытов.
Таблица
| № опыта | I ~, (A) | U~, (B) | Z, (Ом) | I ~, (A) | U~, (B) | R, (Ом) | L, (Гн) |
| без сердечника | |||||||
| по средним | |||||||
| Zср = | Rср = | ||||||
| с сердечником | |||||||
| по средним | |||||||
Задание 1: Измерение индуктивности соленоида.
1. Собрать установку согласно схеме, подключив внешнюю цепь к переменному выходу ИП. Проверить правильность сборки схемы с преподавателем. При разомкнутом ключе К включить входной тумблер ИП для прогревания в течение пяти минут. Катушку индуктивности подключить в цепь соседними клеммами на 1200 витков. Регуляторами вывести вольтметр ИП на ноль.
2. Провести опыт с переменным током. проследив, чтобы внутри катушки не было стального сердечника, замкнуть ключ К и с помощью регулятора ИП установить на измерительном амперметре ток I ~ = 0,3 А. Занести это значение и показание измерительного вольтметра U ~ в первую часть таблицы.
Не меняя режима работы ИП, ввести стальной сердечник в соленоид. Занести показания амперметра и вольтметра во вторую часть таблицы.
3. Повторить опыт, установив в цепи с соленоидом без сердечника значения тока I = 0,5 А и 0,6 А.
4. Подсчитать значение полного сопротивления Zi для каждого опыта по формуле (8). Вычислить средние значения Zср для обеих серий опытов.
5. Разомкнув цепь и выведя индикаторный вольтметр ИП на 0, переключить внешнюю цепь на клеммы постоянного выхода ИП. Заменить измерительные приборы в цепи на соответствующие. Проследить за полярностью их подсоединения.
Проверить схему с преподавателем.
6. Провести опыты при постоянном токе в соответствии с последовательностью п.2 и п.3.
Проанализировать причину отличия результатов этих опытов от опытов при переменном токе. Соображения занести в отчет.
7. Подсчитать значение активного сопротивления Ri и среднее значение Rср.
8. Используя формулу (9), вычислить индуктивность соленоида по средним значениям Rср и Zср.
9. Проанализировать результат этих опытов и записать соображения в «Выводах».
Задание 2: Определить индукцию магнитного поля соленоида.
 Исследования магнитного поля заключаются в определении характеристик этого поля. В условиях данной лабораторной работы возможно определение одной из характеристик поля-индукции магнитного поля соленоида. Как известно, напряженность магнитного поля на оси длинного соленоида:
Исследования магнитного поля заключаются в определении характеристик этого поля. В условиях данной лабораторной работы возможно определение одной из характеристик поля-индукции магнитного поля соленоида. Как известно, напряженность магнитного поля на оси длинного соленоида:
H = I · n = I ·
 Так как
Так как
Для стали μ =800; μ0 = 12,6·10-7 Гн/м
1. 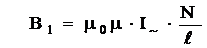 Определить индукцию магнитного поля соленоида с сердечником:
Определить индукцию магнитного поля соленоида с сердечником:
 и без сердечника:
и без сердечника:
в опытах, где сила тока была равна 0,5 А.
2. Сравнить результаты опытов, сделать выводы.
IV. Контрольные вопросы
1. В чем заключается явление электромагнитной индукции? Запишите закон Фарадея.
2. дайте определение магнитному потоку, полному магнитному потоку (потокосцеплению), пронизывающему катушку.
3. Что называется индуктивностью контура, чему равна единица измерения индуктивности.
4. Дайте определение вынужденных электромагнитных колебаний и приведите примеры.
5. Сформулируйте закон Ома для переменного тока и опишите все входящие в него величины.
Не нашли, что искали? Воспользуйтесь поиском: