Упражнение 2. Определение длины волны света

1. Установить собирающую линзу 4 между бипризмой и экраном.

2. Перемещая линзу вдоль оптической скамьи, добиться четкого изображения на экране двух параллельных линий – действительных изображений источников S ₁ и S ₂. Измерить расстояние d' между ними, а также расстояния a между источником S и линзой и b – между линзой и экраном.

3. Вывести линзу из зоны перекрытия волн. Не меняя положения экрана на оптической скамье, измерить ширину интерференционной полосы D _X, взяв расстояние h между тремя-пятью полосами и поделив его на число N светлых полос между ними:

D _X = .

4.Оценить относительную погрешность измерения

= .

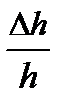5. По формулам (6) и (7) определить длину световой волны.

l = D _X 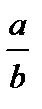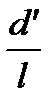, (10)

где l = l ₁ + l ₂.

6. Оценить относительную погрешность измерения l:

= + + + + ,

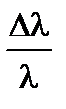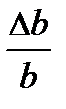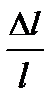где Dl, D a, D b, D(D _X), D d ¢, D l – абсолютные погрешности, соответственно, l, a, b, D _X, d ¢ и l.

7. Определить длину световой волны другим способом. Для этого из формул (6), (8) и (9) находим

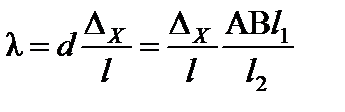(11)

8. Оценим относительную погрешность измерения l.

Учтем, что tg » , так как угол w мал. В этом случае

= + + + .

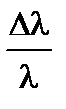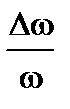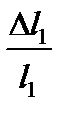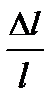Данные измерений и результаты расчётов занести в таблицы 1 и 2.

Таблица 1

АВ×10-3, м	l 1×10-2, м	l 2×10-2, м	w, рад	, %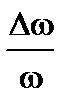

Таблица 2

d '×10-3, м	a ×10-2, м	b ×10-2, м	h ×10-3, м	N	D X ×10-3, м	, %

Сравнить найденные значения l и сделать выводы по результатам эксперимента. Окончательный результат записать в виде:

- по формуле (10): l = …… мкм; = …… %.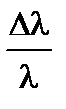

- по формуле (11): l = …… мкм; = …… %.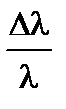

Контрольные вопросы

1. Что называется интерференцией света?

2. Какие источники называются когерентными?

3. Почему невозможно получить интерференционную картину от двух произвольных монохроматических источников света?

4. Как можно получить когерентные источники света?

5. В чем состоит метод получения когерентных источников света с помощью бипризмы Френеля?

6. Каковы условия максимального усиления и ослабления освещенности при интерференции света?

7. Рассмотрите общий случай интерференции волн, исходящих из двух точечных когерентных источников, и выведите формулу для определения длины волны света.

8. Что такое угловая ширина зоны интерференции и ширина интерференционной полосы?

9. Как определяется в данной работе расстояние между мнимыми источниками S ₁ и S ₂?

10. Каким образом можно уменьшить относительную погрешность измерения длины волны света l на данной установке?

Список литературы

1. Савельев И.В. Курс физики. М.: Наука, 1989.-Т.3.

2. Яворский Б.М., Детлаф А.А. Курс физики. – М.: Изд-во «Академия», 2003. – 720 с.

3. Ландсберг Г.С. Оптика. Учебное пособие: Для вузов. – 6-е изд., стереотип. – М.: Физматлит, 2003. – 848 с.

4. Селезнёв В.А., Тимофеев Ю.П. Методические указания к вводному занятию в лабораториях кафедры физики. – М.: МИИТ, 2006. – 30 с.

Работа 302

ИЗУЧЕНИЕ ДИФРАКЦИИ СВЕТА В СХОДЯЩИХСЯ ЛУЧАХ (ДИФРАКЦИЯ ФРЕНЕЛЯ)

Цель работы: изучение дифракционных явлений при распространении сферической световой волны через круглое отверстие в непрозрачном экране.

Приборы и принадлежности: источник света – газовый (He-Ne) лазер, оптическая скамья с сантиметровой шкалой, собирающая линза, диафрагма, отражающий экран, фотоэлемент, микроамперметр.

Введение

При распространении света в среде с резкими неоднородностями наблюдается явление дифракции, то есть нарушение законов геометрической оптики, приводящее к отклонению распространения света от прямолинейного вблизи краев непрозрачных тел. Данное явление обусловлено волновой природой света. В случае, когда дифракция наблюдается в сходящихся (непараллельных) лучах, говорят о дифракции Френеля.

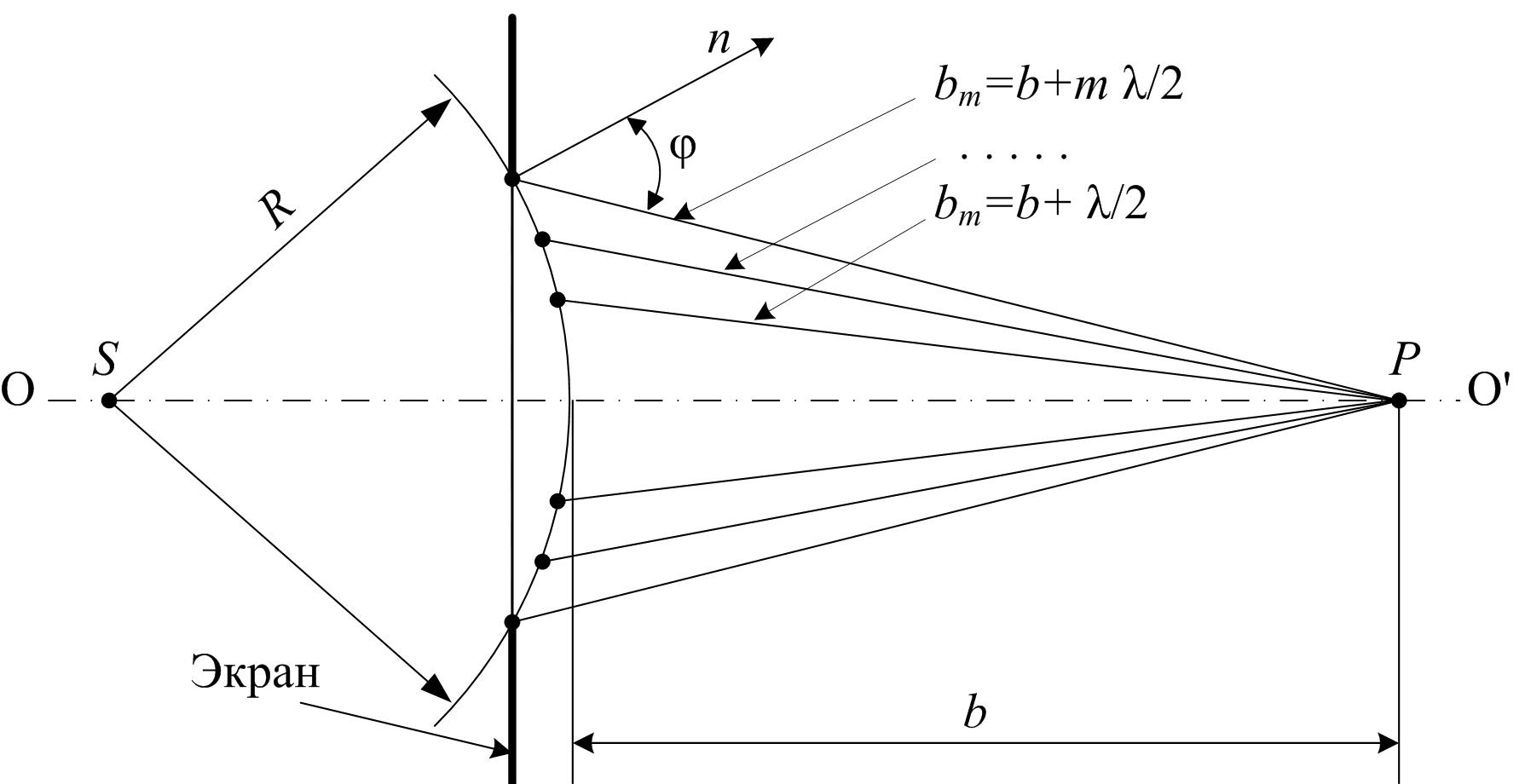
Рис. 1

Рассмотрим дифракцию Френеля на примере распространения сферической световой волны через круглое отверстие в непрозрачном экране. Для того, чтобы определить действие световой волны в какой-либо точке Р на линии ОО ' (рис. 1), воспользуемся методом зон Френеля. Разобьем открытую волновую поверхность на кольцевые зоны Френеля, построенные таким образом, чтобы расстояние от краев соседних зон до точки Р отличалось на половину длины волны λ/2.

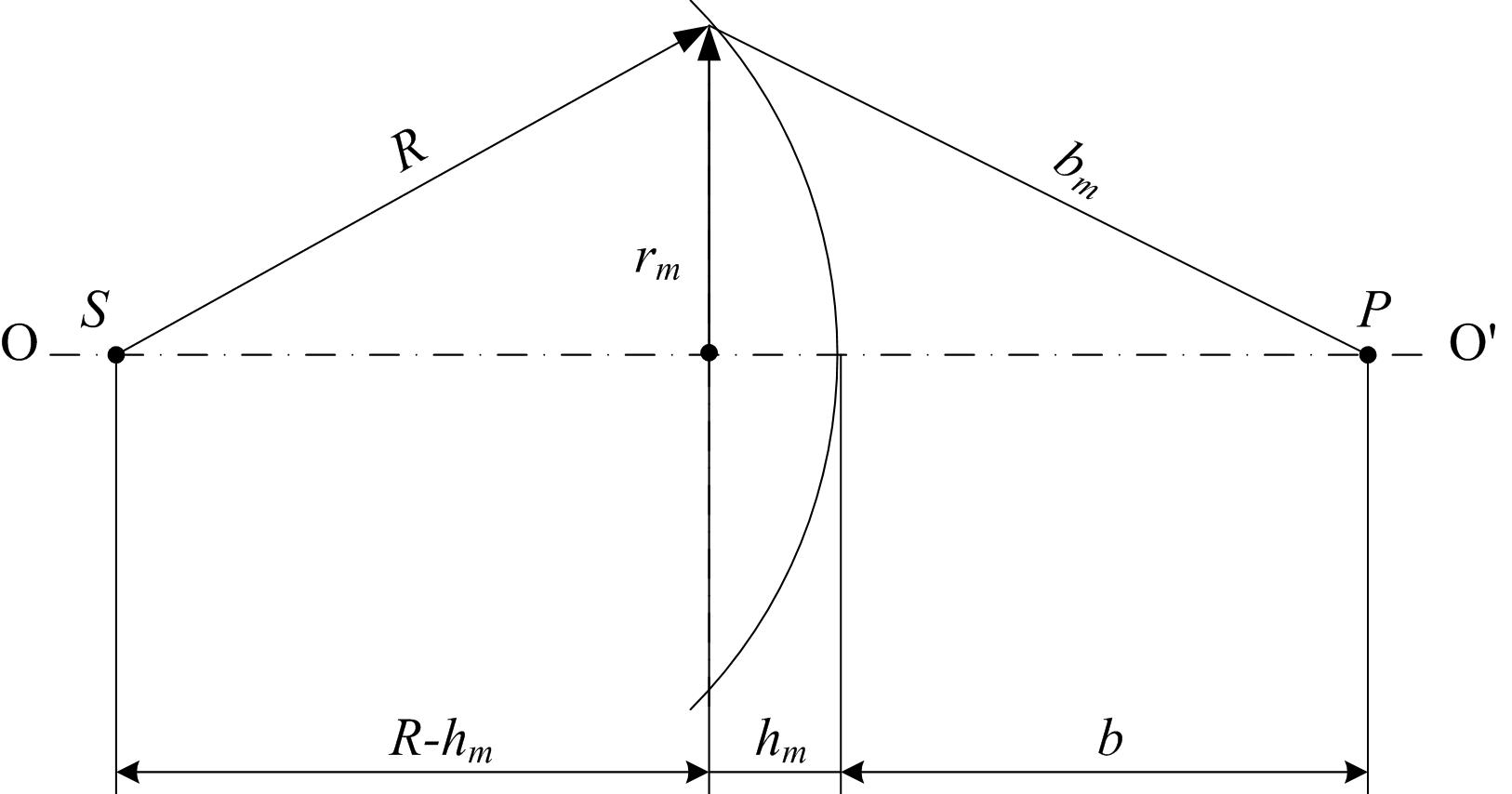
Рис. 2

Определим площади и радиусы зон Френеля. Согласно рис. 2, имеет место соотношение

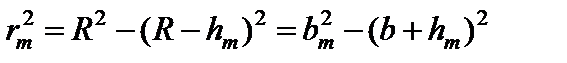, (1)

где r_m – радиус зоны Френеля под номером m;

R – радиус волновой поверхности;

h_m – высота сферического сегмента, выделяемого внешней границей m -й зоны;

b – расстояние от волновой поверхности до точки наблюдения P;

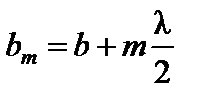– расстояние от точки P до границы зоны Френеля под номером m.

Ввиду малости λ при небольших значениях m можно пренебречь слагаемым, содержащим λ². С учетом этого приближения из формулы (1) следует

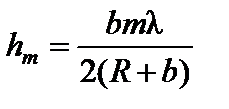(2)

Так как площадь сферического сегмента S_m = 2p R h_m, выражение для площади m -й зоны имеет вид

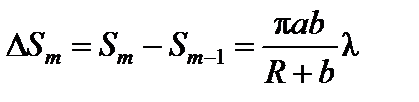. (3)

Следовательно, площади зон Френеля примерно одинаковы (Δ S_m не зависит от m).

Полагая h_m << R, из соотношения (1) получим для радиуса зоны Френеля под номером m выражения r_m =2 Rh_m, или с учетом (2),

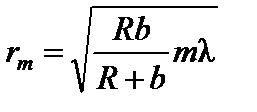. (4)

Очевидно, если r_m является одновременно радиусом r рассматриваемого отверстия в экране, то оно открывает часть волнового фронта, на котором умещается число зон Френеля, равное

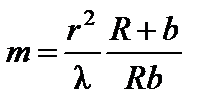. (5)

Интенсивность света в точке наблюдения Р зависит от числа m открытых зон Френеля. Колебания, возбуждаемые в точке Р вторичными источниками от аналогичных участков соседних зон, будут находиться в противофазе, то есть ослаблять друг друга (по определению расстояния до указанных участков от точки Р отличаются на λ / 2). Следовательно, если отверстие открывает четное число зон Френеля, в точке Р наблюдается минимум освещенности, нечетное – максимум.

Амплитуды колебаний, возбуждаемых зонами в точке Р, в соответствии с принципом Гюйгенса-Френеля образуют монотонно убывающую последовательность

A₁ > А₂ >... > A _{m -1} >A _m > A _{m +1} >...

Это связано с тем, что площади зон примерно одинаковы, а расстояния b_m от зоны до точки наблюдения Р увеличиваются с ростом m. Кроме того, от центральной зоны к периферическим увеличивается угол j между нормалью к элементам зоны и направлением на точку Р (см. рис. 1). Амплитуда результирующего колебания равна алгебраической сумме амплитуд:

A = A ₁- A ₁+ A ₃- A ₄+... (6)

Здесь знак минус учитывает, что фазы колебаний, возбуждаемые соседними зонами, отличаются на p.

Преобразуем выражение (6) к виду

(7)

Вследствие монотонного убывания А_m можно приближенно считать, что 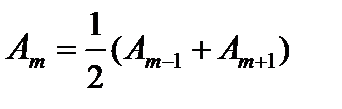. Тогда выражения в скобках будут равны нулю, и амплитуда колебания в точке Р, возбуждаемого полностью открытым волновым фронтом, окажется равной А = A ₁ / 2. Если отверстие открывает только одну центральную зону Френеля, то амплитуда колебания равна А = А ₁, то есть в два раза больше. Соответственно интенсивность I в точке Р (которая пропорциональна квадрату амплитуды) при одной открытой зоне в четыре раза больше, чем при полностью открытом волновом фронте так как I ~ А ² [2].

Как следует из соотношения (5), при фиксированных длине волны излучения λ, размерах отверстия r и расстоянии между источником света S и точкой наблюдения Р освещенность в точке Р будет зависеть от положения экрана – расстояний R и b.

Описание установки

Схема установки приведена на рис. 3. На одном конце оптической скамьи располагается источник света – (He - Ne) лазер 1, дающий монохроматическое излучение с длиной волны λ = 0,628 мкм (рис. 3). Луч лазера с помощью собирающей линзы 2 фокусируется в точку S и далее распространяется в виде сферической волны. На некотором расстоянии от точки S располагается рейтер 3 с ирисовой диафрагмой так, что ее центр совпадает с оптической осью установки.

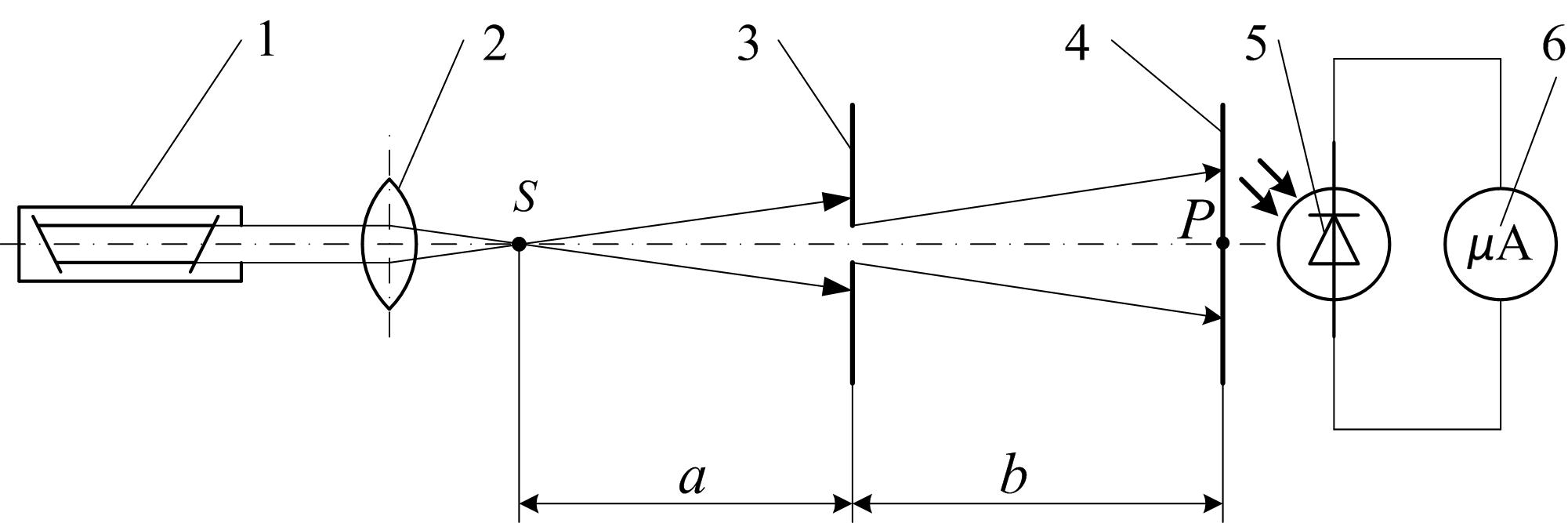
Рис. 3

Диафрагма представляет собой круглое отверстие переменного диаметра. Диаметр отверстия регулируется поворотом рычага диафрагмы. На другом конце оптической скамьи помещается экран 4 для наблюдения дифракционной картины и фотоэлемент 5, предназначенный для измерения освещенности. Сила тока в цепи фотоэлемента пропорциональна интенсивности света, и может быть измерена с помощью микроамперметра 6 (mA).

Для измерения расстояния между диафрагмой и точечным источником S используется сантиметровая шкала оптической скамьи, начало отсчета, которой совпадает с положением источника сферической волны.

Не нашли, что искали? Воспользуйтесь поиском: