
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Цикл с изохорным подводом теплоты, изобарным расширеним и политропным сжатием
Выполним расчёт и анализ указанного цикла на примере решения следующей задачи.
Задача.
1 кг воздуха, находящегося при температуре минус 10,3 °С и разрежении 50 мм рт. ст., изохорно нагревается до манометрического давления 1,0 кгс/см2, а затем изобарно расширяется до такого объёма, чтобы политропно возвратиться в начальное состояние. Показатель политропы п = –1,3. Атмосферное давление 100,5 кПа.
Определить параметры воздуха в характерных точках цикла, а также степень его термодинамического совершенства. Изобразить цикл, образованный указанными процессами, на термических и тепловой диаграммах.
Решение
Термические параметры рабочего тела (воздуха) в характерных точках цикала:
Точка 1
- давление
 ,
,
так как 750 мм рт. ст. = 1 бар
- температура 
- удельный объем 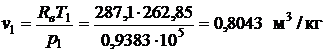 ,
,
где  – удельная газовая постоянная воздуха.
– удельная газовая постоянная воздуха.
Точка 2
- давление
 ,
,
так как 1 кг/см2 = 98066,5 Па;
- удельный объем
 , (по условию задачи процесс 1-2 изохорный);
, (по условию задачи процесс 1-2 изохорный);
- температура
 ®
®  .
.
Точка 3
- давление (по условию процесс 2-3 изобарный)  ;
;
- удельный объем (процесс 3-1 политропный).

 ®
® 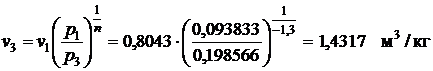 ;
;
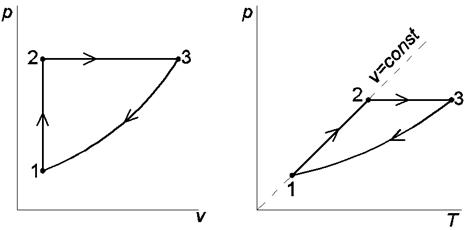

Рис.1.3. Изображения заданного цикла на термических
и тепловой диаграммах:
1-2 – изохорный подвод теплоты; 2-3 – изобарное расширение;
3-1 – политропное сжатие
- температура

 .
.
Результаты расчетов записываем в таблицу
| Точки | р, МПа | v, м3/кг | Т, К |
| 0,09383 | 0,8042 | 262,85 | |
| 0,19857 | 0,8042 | 556,25 | |
| 0,19857 | 1,4317 | 990,19 |
Отводимая в цикле теплота
 ,
,
где изохорная теплоёмкость сv по упрощенной МКТ для воздуха, как двухатомного газа, рассчитывается из соотношения
 .
.
Подводимая в цикле теплота
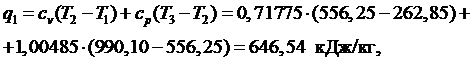
где изобарная теплоёмкость ср в соответствии с МКТ равна
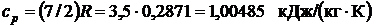 .
.
Термический КПД рассматриваемого цикла
 .
.
Термический КПД предельного цикла Карно

Степень совершенства рассчитанного цикла
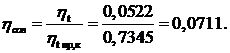
Итак, рассмотренный термодинамический цикл значительно уступает по эффективности соответствующему предельному циклу Карно. Это обусловлено тем, что количества подводимой и отводимой теплоты в цикле близки.
1.4. Цикл с адиабатным сжатием, изохорным подводом теплоты, изобарным и политропным расширением
Выполним исследование заданной совокупности процессов на примере решения следующей задачи.
Задача
1 нм3 метана адиабатно сжимается до 1/5 первоначального объема, затем изохорно нагревается при подводе 200 кДжтеплоты, затем изобарно расширяется с подводом 100 кДж теплоты, наконец, политропно возвращается в начальное состояние.
Изобразить цикл на термических и тепловой диаграммах. Определить параметры газа в характерных точках образовавшегося цикла и его степень совершенства. Начальные параметры рабочего тела р 1= 1 бар, t 1 = 100 °С.
Решение
Прежде всего, изобразим цикл на диаграммах состояния (рис.1.4).
Затем рассчитываем:
- удельную газовую постоянную метана (СН4)
 ;
;
- удельный объем метана в точке 1
 ;
;
- параметры метана в точке 2 (процесс 1-2 – адиабатный):
удельный объём  ;
;
температура  ;
;
давление  ,
,
где k = 1,33 – показатель адиабаты для газов, молекулы которых содержат три и большее количество атомов.


Рис. 1.4. Изображения исследуемого цикла на термических
и тепловой диаграммах:
1-2 – адиабатное сжатие; 2-3 – изохорный подвод теплоты;
3-4 – изобарный подвод теплоты; 4-1 – политропный отвод теплоты
Для дальнейших расчетов необходимо определить массу одного нм3 метана из уравнения состояния идеального газа
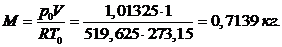
При определении параметров точки 3 используем заданное значение теплоты, подводимой в процессе. Удельная теплота в изохорном процессе 2-3 рассчитывается из соотношения
 , тогда
, тогда  ,
,
где qv = Qv / М = 200/0,7139 = 280,15 кДж/кг – удельная теплота, подводимая в изохорном процессе;
cv – изохорная теплоёмкость сv, которая по упрощенной МКТ рассчитывается из соотношения
 ,
,
где j – количество вращательных степеней свободы атомов в молекуле (для трёх- и многоатомных газов j = 3).
В изохорном процессе температура и давление изменяются прямо пропорционально
 , отсюда
, отсюда  .
.
Параметры точки 4 ( процесс 3-4 –изобарный)
р4 = р3 = 1,0912 МПа.
Удельная теплота в изобарном процессе рассчитывается из соотношения
 ,
,
отсюда  ,
,
где qp = Qp/М = 100/0,7139 = 140,08 кДж/кг – удельная теплота, подводимая в изобарном процессе (см. условие задачи),
cp – изобарная теплоёмкость метана, рассчитываемая из соотношения
 .
.
В изобарном процессе температура и удельный объём изменяются прямо пропорционально
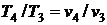 , отсюда
, отсюда 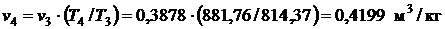 .
.
Результаты расчетов записываем в таблицу
| Точки | р, МПа | v, м3/кг | Т, К |
| 0,1 | 1,9390 | 373,15 | |
| 0,8504 | 0,3878 | 634,66 | |
| 1,0912 | 0,3878 | 814,37 | |
| 1,0912 | 0,4199 | 881,76 |
Критерием точности выполненных расчётов является равенство суммы работΣ l, рассчитанных через параметры p и v и суммы теплот Σ q, рассчитанных через Т, ср и сv для всех процессов, образующих цикл.
Рассчитываем значения деформационной работы во всех термодинамических процессах, образующих исследуемый цикл:
– работа в адиабатном процессе сжатия 1-2

– работа в изохорном процессе 2-3  ;
;
– работа расширения в изобарном процессе 3-4
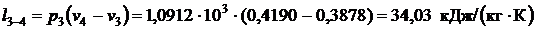 ;
;
– работа в политропном процессе расширения 4-1
 ,
,
где п – показатель политропы расширения, рассчитанный из соотношения
 , отсюда
, отсюда 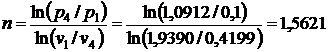 .
.
Далее рассчитываем значения теплоты в процессах, образующих цикл:
– в адиабатном процессе сжатия 1-2  ;
;
– в изохорном процессе 2-3 ( см. стр.19 )  ;
;
– в изобарном процессе 3-4 (стр.20)  ;
;
– в политропном процессе 4-1
 .
.
Результаты расчетов сводим в следующую таблицу:
| Процессы | Деформационная работа l, кДж/кг | Теплота q, кДж/кг |
| 1-2 – адиабатный | –411,78 | 0. |
| 2-3 – изохорный | 0. | 280,15 |
| 3-4 – изобарный | 34,05 | 140,08 |
| 4-1 – политропный | 470,19 | –327,39 |
| Сумма | 92,46 | 92,84 |
Из таблицы видно, что сумма работ отличается от суммы теплот на 0,38 кДж/кг, то есть на 0,41 %. Это свидетельствует об удовлетворительной точности расчетов.
Термический КПД исследуемого цикла
 ,
,
где q 1 = q 2-3 + q 3-4 = 280,15 + 140,08 = 420,23 кДж/кг – теплота, подводимая в цикле.
Термический КПД предельного цикла Карно
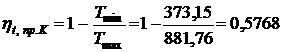 .
.
Степень совершенства рассматриваемого цикла
 .
.
Следовательно, эффективность заданного цикла ниже эффективности соответствующего предельного цикла Карно почти на 62 %.
Не нашли, что искали? Воспользуйтесь поиском: