
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Центрально-растянутые и центрально-сжатые элементы
4.1. Расчет центрально-растянутых элементов следует производить по формуле
 , (4)
, (4)
где N – расчетная продольная сила;
R p – расчетное сопротивление древесины растяжению вдоль волокон;
F нт – площадь поперечного сечения элемента нетто.
При определении F нт ослабления, расположенные на участке длиной до 200 мм, следует принимать совмещенными в одном сечении.
4.2. Расчет центрально-сжатых элементов постоянного цельного сечения следует производить по формулам:
а) на прочность
 ; (5)
; (5)
б) на устойчивость
 , (6)
, (6)
где R с – расчетное сопротивление древесины сжатию вдоль волокон;
j – коэффициент продольного изгиба, определяемый согласно п. 4.3;
F нт – площадь нетто поперечного сечения элемента;
F рас – расчетная площадь поперечного сечения элемента, принимаемая равной:
при отсутствии ослаблений или ослаблениях в опасных сечениях, не выходящих на кромки (рис. 1, а), если площадь ослаблений не превышает 25% Е бр, Е расч = F бр, где F бр – площадь сечения брутто; при ослаблениях, не выходящих на кромки, если площадь ослабления превышает 25% F бр, F рас = 4/3 F нт; при симметричных ослаблениях, выходящих на кромки (рис. 1, б), F рас = F нт.

4.3. Коэффициент продольного изгиба j следует определять по формулам (7) и (8);
при гибкости элемента l £ 70
 ; (7)
; (7)
при гибкости элемента l > 70
 , (8)
, (8)
где коэффициент а = 0,8 для древесины и а = 1 для фанеры;
коэффициент А = 3000 для древесины и А = 2500 для фанеры.
4.4. Гибкость элементов цельного сечения определяют по формуле
 , (9)
, (9)
где l о – расчетная длина элемента;
r – радиус инерции сечения элемента с максимальными размерами брутто соответственно относительно осей Х и У.
4.5. Расчетную длину элемента l о следует определять умножением его свободной длины l на коэффициент m0
l о = l m0 (10)
согласно пп. 4.21 и 6.25.
4.6. Составные элементы на податливых соединениях, опертые всем сечением, следует рассчитывать на прочность и устойчивость по формулам (5) и (6), при этом F нт и F рас определять как суммарные площади всех ветвей. Гибкость составных элементов l следует определять с учетом податливости соединений по формуле
 , (11)
, (11)
где lу – гибкость всего элемента относительно оси У (рис. 2), вычисленная по расчетной длине элемента l о без учета податливости;
l1 – гибкость отдельной ветви относительно оси I–I (см. рис. 2), вычисленная по расчетной длине ветви l 1; при l 1 меньше семи толщин (h 1) ветви принимаются l1 = 0;
mу – коэффициент приведения гибкости, определяемый по формуле
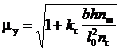 , (12)
, (12)
где b и h – ширина и высота поперечного сечения элемента, см:
n ш – расчетное количество швов в элементе, определяемое числом швов, по которым суммируется взаимный сдвиг элементов (на рис. 2, а – 4 шва, на рис. 2, б – 5 швов);
l о – расчетная длина элемента, м;
n с – расчетное количество срезов связей в одном шве на 1 м элемента (при нескольких швах с различным количеством срезов следует принимать среднее для всех швов количество срезов);
k с – коэффициент податливости соединений, который следует определять по формулам табл. 12.
Таблица 12
| Коэффициент k c при | ||
| Вид связей | центральном сжатии | сжатии с изгибом |
| 1. Гвозди | 10 d 2 | 5 d 2 |
| 2. Стальные цилиндрические нагели | 5 d 2 | 2,5 d 2 |
| а) диаметром £ 1/7 толщины соединяемых элементов | 5 d 2 | 1 2,5 d 2 |
| б) диаметром > 1/7 толщины соединяемых элементов | 1,5 ad | ad |
| 3. Дубовые цилиндрические нагели | 1 d 2 | 1,5 d 2 |
| 4. Дубовые пластинчатые нагели | _ | 1,4 d b пл |
| 5. Клей | 0 |
Примечание. Диаметры гвоздей и нагелей d, толщину элементов а, ширину b пл и толщину d пластинчатых нагелей следует принимать в см.

При определении k с диаметр гвоздей следует принимать не более 0,1 толщины соединяемых элементов. Если размер защемленных концов гвоздей менее 4 d, то срезы в примыкающих к ним швах в расчете не учитывают. Значение k с соединений на стальных цилиндрических нагелях следует определять по толщине а более тонкого из соединяемых элементов.
При определении k с диаметр дубовых цилиндрических нагелей следует принимать не более 0,25 толщины более тонкого из соединяемых элементов.
Связи в швах следует расставлять равномерно по длине элемента. В шарнирно-опертых прямолинейных элементах допускается в средних четвертях длины ставить связи в половинном количестве, вводя в расчет по формуле (12) величину n с, принятую для крайних четвертей длины элемента.
Гибкость составного элемента, вычисленную по формуле (11), следует принимать не более гибкости l отдельных ветвей, определяемой по формуле
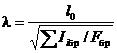 , (13)
, (13)
где å Ii бр – сумма моментов инерции брутто поперечных сечений отдельных ветвей относительно собственных осей, параллельных оси У (см. рис. 2);
F бр – площадь сечения брутто элемента;
l о – расчетная длина элемента.
Гибкость составного элемента относительно оси, проходящей через центры тяжести сечений всех ветвей (ось Х на рис. 2), следует определять как для цельного элемента, т. е. без учета податливости связей, если ветви нагружены равномерно. В случае неравномерно нагруженных ветвей следует руководствоваться п. 4.7.
Если ветви составного элемента имеют различное сечение, то расчетную гибкость l1 ветви в формуле (11) следует принимать равной:
 , (14)
, (14)
определение l 1 приведено на рис. 2.
4.7. Составные элементы на податливых соединениях, часть ветвей которых не оперта по концам, допускается рассчитывать на прочность и устойчивость по формулам (5), (6) при соблюдении следующих условий:
а) площади поперечного сечения элемента F нт и F рас следует определять по сечению опертых ветвей;
б) гибкость элемента относительно оси У (см. рис. 2) определяется по формуле (11); при этом момент инерции принимается с учетом всех ветвей, а площадь – только опертых;
в) при определении гибкости относительно оси Х (см. рис. 2) момент инерции следует определять по формуле
I = I о + 0,5 I но, (15)
где I о и I но – моменты инерции поперечных сечений соответственно опертых и неопертых ветвей.
4.8. Расчет на устойчивость центрально-сжатых элементов переменного по высоте сечения следует выполнять по формуле
 , (16)
, (16)
где F макс – площадь поперечного сечения брутто с максимальными размерами;
k ж N – коэффициент, учитывающий переменность высоты сечения, определяемый по табл. 1 прил. 4 (для элементов постоянного сечения k ж N = 1);
j – коэффициент продольного изгиба, определяемый по п. 4.3 для гибкости, соответствующей сечению с максимальными размерами.
Изгибаемые элементы
4.9. Расчет изгибаемых элементов, обеспеченных от потери устойчивости плоской формы деформирования (см. пп. 4.14 и 4.15), на прочность по нормальным напряжениям следует производить по формуле
 , (17)
, (17)
где М – расчетный изгибающий момент;
R и – расчетное сопротивление изгибу;
W рас – расчетный момент сопротивления поперечного сечения элемента. Для цельных элементов W рас = W нт; для изгибаемых составных элементов на податливых соединениях расчетный момент сопротивления следует принимать равным моменту сопротивления нетто W нт, умноженному на коэффициент k w; значения k w для элементов, составленных из одинаковых слоев, приведены в табл. 13. При определении W нт ослабления сечений, расположенные на участке элемента длиной до 200 мм, принимают совмещенными в одном сечении.
Таблица 13
| Обозначение коэф- | Число слоев | Значение коэффициентов для расчета изгибаемых составных элементов при пролетах, м | |||
| фициентов | в элементе | 9 и более | |||
| 0,7 | 0,85 | 0,9 | 0,9 | ||
| k w | 0,6 | 0,8 | 0,85 | 0,9 | |
| 0,4 | 0,7 | 0,8 | 0,85 | ||
| 0,45 | 0,65 | 0,75 | 0,8 | ||
| k ж | 0,25 | 0,5 | 0,6 | 0,7 | |
| 0,07 | 0,2 | 0,3 | 0,4 |
Примечание. Для промежуточных значений величины пролета и числа слоев коэффициенты определяются интерполяцией.
4.10. Расчет изгибаемых элементов на прочность по скалыванию следует выполнять по формуле
 , (18)
, (18)
где Q – расчетная поперечная сила;
S бр – статический момент брутто сдвигаемой части поперечного сечения элемента относительно нейтральной оси;
I бр – момент инерции брутто поперечного сечения элемента относительно нейтральной оси;
b рас – расчетная ширина сечения элемента;
R ск – расчетное сопротивление скалыванию при изгибе.
4.11. Количество срезов связей n с, равномерно расставленных в каждом шве составного элемента на участке с однозначной эпюрой поперечных сил, должно удовлетворять условию
 , (19)
, (19)
где Т – расчетная несущая способность связи в данном шве;
М А, М В – изгибающие моменты в начальном А и конечном В сечениях рассматриваемого участка.
Примечание. При наличии в шве связей разной несущей способности, но одинаковых по характеру работы (например, нагелей и гвоздей), несущие способности их следует суммировать.
4.12. Расчет элементов цельного сечения на прочность при косом изгибе следует производить по формуле
 , (20)
, (20)
где М х и М у – составляющие расчетного изгибающего момента для главных осей сечения Х и У;
W x и W у – моменты сопротивлений поперечного сечения нетто относительно главных осей сечения Х и У.
4.13. Клееные криволинейные элементы, изгибаемые моментом М, уменьшающим их кривизну, следует проверять на радиальные растягивающие напряжения по формуле
 , (21)
, (21)
где s0 – нормальное напряжение в крайнем волокне растянутой зоны;
s i – нормальное напряжение в промежуточном волокне сечения, для которого определяются радиальные растягивающие напряжения;
hi – расстояние между крайним и рассматриваемым волокнами;
ri – радиус кривизны линии, проходящей через центр тяжести части эпюры нормальных растягивающих напряжений, заключенной между крайним и рассматриваемым волокнами;
R р.90 – расчетное сопротивление древесины растяжению поперек волокон, принимаемое по п. 7 табл. 3.
4.14. Расчет на устойчивость плоской формы деформирования изгибаемых элементов прямоугольного постоянного сечения следует производить по формуле
 , (22)
, (22)
где М – максимальный изгибающий момент на рассматриваемом участке l р;
W бр – максимальный момент сопротивления брутто на рассматриваемом участке l p.
Коэффициент jМ для изгибаемых элементов прямоугольного постоянного поперечного сечения, шарнирно-закрепленных от смещения из плоскости изгиба и закрепленных от поворота вокруг продольной оси в опорных сечениях, следует определять по формуле
 , (23)
, (23)
где l p – расстояние между опорными сечениями элемента, а при закреплении сжатой кромки элемента в промежуточных точках от смещения из плоскости изгиба – расстояние между этими точками;
b – ширина поперечного сечения;
h – максимальная высота поперечного сечения на участке l p;
k ф – коэффициент, зависящий от формы эпюры изгибающих моментов на участке l p, определяемый по табл. 2 прил. 4 настоящих норм.
При расчете изгибаемых элементов с линейно меняющейся по длине высотой и постоянной шириной поперечного сечения, не имеющих закреплений из плоскости по растянутой от момента М кромке, или при m < 4 коэффициент j М по формуле (23) следует умножать на дополнительный коэффициент k ж М . Значения k ж М приведены в табл. 2 прил. 4. При m ³ 4 k ж М = 1.
При подкреплении из плоскости изгиба в промежуточных точках растянутой кромки элемента на участке l p коэффициент j М определенный по формуле (23), следует умножать на коэффициент k п М :
 , (24)
, (24)
где ap – центральный угол в радианах, определяющий участок l p элемента кругового очертания (для прямолинейных элементов ap = 0);
m – число подкрепленных (с одинаковым шагом) точек растянутой кромки на участке l p (при m ³ 4 величину 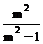 следует принимать равной 1).
следует принимать равной 1).
4.15. Проверку устойчивости плоской формы деформирования изгибаемых элементов постоянного двутаврового или коробчатого поперечного сечений следует производить в тех случаях, когда
l p ³ 7 b, (25)
где b – ширина сжатого пояса поперечного сечения.
Расчет следует производить по формуле
 , (26)
, (26)
где j – коэффициент продольного изгиба из плоскости изгиба сжатого пояса элемента, определяемый по п. 4.3;
R с – расчетное сопротивление сжатию;
W бр – момент сопротивления брутто поперечного сечения; в случае фанерных стенок – приведенный момент сопротивления в плоскости изгиба элемента.
Не нашли, что искали? Воспользуйтесь поиском: