
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Теоретическая часть. 3. Экспериментальная установка……….…………………………………8
Содержание
1. Цель работы………………………………………………………………4
2. Теоретическая часть….………………………………………………….4
3. Экспериментальная установка……….…………………………………8
4. Порядок выполнения работы……………………………………………9
5. Требования к отчету……………………………………………………10
6. Контрольные вопросы………………………………………………….11
Список литературы…..…………………………………………….…..11
Лабораторная работа № 116
Определение отношения теплоемкостей газа
При постоянном давлении и объеме
Цель работы
Изучение закономерностей изменения параметров состояния газа в различных процессах и определение отношения теплоемкостей воздуха при постоянном давлении и объеме.
Теоретическая часть
Удельной теплоемкостью вещества называется величина, равная количеству теплоты, которую надо сообщить единице массы этого вещества для увеличения его температуры на один градус, а молярной теплоемкостью – количество теплоты, которое необходимо сообщить одному молю вещества для нагревания его на один градус. Если при передаче телу количества теплоты δ Q его температура увеличится на dT градусов, то по определению удельная теплоемкость С будет равна:
 , (2.1)
, (2.1)
где m – масса тела, а молярная теплоемкость –
 , (2.2)
, (2.2)
где ν – количество молей вещества.
Удельная и молярная теплоемкости газов зависят как от природы газа, так и от условий его нагревания. Это непосредственно следует из первого закона термодинамики, согласно которому количество теплоты, переданное системе, равно сумме изменения ее внутренней энергии du и совершенной ею работы δ А над внешними телами:
 . (2.3)
. (2.3)
Изменение внутренней энергии идеального газа однозначно определяется его начальным и конечным состояниями, тогда как совершаемая газом работа зависит от характера происходящего с ним процесса и может быть разной по величине и по знаку. Следовательно, теплоемкость газа для различных процессов будет разной. Однако для конкретного процесса как молярная, так и удельная теплоемкость газа имеет строго определенное значение и является однозначной характеристикой газа в данном процессе.
Нагревание газа при постоянном объеме не сопровождается совершением работы (δ А = 0) и вся теплота идет на изменение его внутренней энергии, которая в соответствии с законом равнораспределения энергии теплового движения по степеням свободы молекул газа при изменении его температуры на dT равно:
 , (2.4)
, (2.4)
где R – газовая постоянная; а i – сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекул газа. В условиях, с которыми сталкиваются на практике, последнее можно исключить, поскольку колебательное тепловое движение в молекулах возбуждается только при достаточно высоких (больше 1000 К) температурах и полагать i = 3 для одноатомных молекул, i = 5 – для линейных молекул и i =6 – для остальных.
Следуя (2.2), (2.3) и (2.4), получаем, что молярная теплоемкость газа при постоянном объеме равна:
 . (2.5)
. (2.5)
При нагревании газа на dT градусов при постоянном давлении им будет совершаться работа
 , (2.6)
, (2.6)
и его молярная теплоемкость при постоянном давлении оказывается равной
 . (2.7)
. (2.7)
Отношение теплоемкости газа при постоянном давлении к теплоемкости при постоянном объеме называют коэффициентом Пуассона или показателем адиабаты газа:
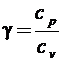 . (2.8)
. (2.8)
Из (2.5) и (2.7) следует, что коэффициент Пуассона газа определяется только числом степеней свободы его молекул:
 . (2.9)
. (2.9)
Рассмотрим сосуд, который может через кран сообщаться с атмосферой. Если подкачать в него воздух и подождать до установления теплового равновесия с окружающей средой, то после этого воздух в сосуде будет иметь давление Р 1, превышающее атмосферное давление Р 0 на некоторую величину Δ Р 1, и температуру Т 1, равную температуре окружающей среды Т 0. Если теперь на короткое время открыть кран, то давление в сосуде упадет до атмосферного, а температура понизится до некоторого значения Т 2. При этом часть воздуха из сосуда быстро выйдет, а оставшийся воздух, занимавший в сосуде объем V 1, займет весь объем сосуда V 2, т.е. этот воздух из состояния 1 с параметрами  и Т 1 = Т 0 перейдет в состояние 2 с параметрами Р 2 = Р 0, V 2 и Т 2. Этот переход происходит настолько кратковременно, что воздух в сосуде не успевает получить тепло от окружающей среды, поэтому его можно считать адиабатным процессом, подчиняющимся закону Пуассона:
и Т 1 = Т 0 перейдет в состояние 2 с параметрами Р 2 = Р 0, V 2 и Т 2. Этот переход происходит настолько кратковременно, что воздух в сосуде не успевает получить тепло от окружающей среды, поэтому его можно считать адиабатным процессом, подчиняющимся закону Пуассона:
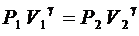 или
или  , (2.10)
, (2.10)
согласно которому
 . (2.11)
. (2.11)
После закрытия крана охлажденный вследствие адиабатного расширения воздух в сосуде начнет нагреваться при постоянном объеме за счет притока тепла извне. В итоге он займет состояние 3 с температурой, равной температуре окружающей среды (Т 3= Т 0). При этом давление его повысится до  . Для изохорного процесса можно применить закон Шарля:
. Для изохорного процесса можно применить закон Шарля:
 . (2.12)
. (2.12)
Учитывая, что Т 1 = Т 3= Т 0, а Р 2 = Р 0, из уравнений (2.11) и (2.12) имеем:
 . (2.13)
. (2.13)
Логарифмируя это равенство, получаем:
 , (2.14)
, (2.14)
откуда  . (2.15)
. (2.15)
Если избыточные давления Δ Р 1 и Δ Р 3 значительно меньше атмосферного Р 0, то  «1 и
«1 и  «1. В этом случае можно воспользоваться тем, что при х «1
«1. В этом случае можно воспользоваться тем, что при х «1  ≃ х и представить уравнение (2.15) в более простом виде:
≃ х и представить уравнение (2.15) в более простом виде:
 . (2.16)
. (2.16)
При измерении избыточных давлений с помощью жидкостного U – образного манометра:
 и
и 
 ,
,  (2.17)
(2.17)
где r – плотность жидкости; g – ускорение свободного падения, а H и h – соответствующие Δ Р 1 и Δ Р 3 разности высот уровней жидкости в коленах манометра. Подставляя (2.17) в (2.16), в случае малых избыточных давлений получаем следующую расчетную формулу для γ:
 . (2.18)
. (2.18)
Рассмотренный метод определения γ был в свое время предложен Клеманом и Дезормом.
Не нашли, что искали? Воспользуйтесь поиском: