Теоретическая часть. Определение удельной и молярной теплоты парообразования воды при фазовом переходе первого рода по экспериментально полученной зависимости давления насыщенных

Цель работы

Определение удельной и молярной теплоты парообразования воды при фазовом переходе первого рода по экспериментально полученной зависимости давления насыщенных паров от температуры.

Теоретическая часть

Фазой называется термодинамически равновесное состояние вещества, имеющая границу с другими частями системы, в которой она находится, и отличающееся по физическим свойствам от других возможных равновесных состояний того же вещества. Фазовый переход первого рода всегда сопровождается поглощением или выделением скрытой теплоты Q и изменением удельного объема и молярного объема μ υ вещества, μ υ = , где – число молей; , m – масса, μ – молярная масса вещества.

Поскольку количество скрытой теплоты зависит от массы вещества, претерпевающей фазовый переход, для характеристики процесса используется удельная теплота перехода q, отнесенная к единице массы вещества:

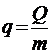, (2.1)

и молярная теплота перехода μ q, отнесенная к одному молю вещества:

. (2.2)

При постоянном давлении фазовый переход всегда проходит при определенной температуре, называемой температурой перехода, при которой возможно термодинамическое равновесие фаз при данном давлении. Для рассмотрения фазового перехода «жидкость – пар» обратимся к изотермам, построенным для нескольких значений температуры (Т ₁, Т ₂) на P – V диаграмме рис.2.1.

Рис.2.1. Изотермы Ван-дер-Ваальса и реального вещества

Горизонтальные участки изотерм отвечают областям фазового перехода. В процессе перехода молярный объем скачкообразно изменяется от величины , что соответствует молярному объему жидкой фазы, до величины , что соответствует молярному объему газообразной фазы. Любая точка с координатами p и , находящаяся справа от кривой EDB, соответствует газообразному состоянию. Любая другая точка с координатами p' и , расположенная слева от кривой ECA, соответствует жидкому состоянию вещества. Все точки, лежащие внутри кривой ACEDB, соответствуют двухфазным состояниям, т.е. состояниям, при которых одновременно существует жидкость и насыщенный пар над ней. Интервал – представляет собой область двухфазного состояния (жидкость – пар) вещества. Среди всех возможностей температур есть одна, называемая критической температурой Т _кр, при которой горизонтальный участок изотермы, что отвечает фазовому переходу, вырождается в точку перегиба (точка E на рис.2.1). При температуре вещества, больше критической, исчезает разница между паром и жидкостью, а вещество ни при каком давлении невозможно перевести из газообразного в жидкое состояние. За областью фазового перехода состояние реального вещества в жидкой и газообразной фазах достаточно точно описывает уравнение Ван-дер-Ваальса, которое для одного моля газа имеет вид

(2.3)

где а и b введены для учета потенциального взаимодействия между молекулами и собственного объема газа. Изотерма, описываемая уравнением Ван-дер-Ваальса на P – V диаграмме для температуры Т ₁, изображена на рис.2.1 штрихпунктирной линией.

Для вычисления изменения давления насыщенного пара в зависимости от температуры проведем для одного моля вещества цикл Карно, в который входят горизонтальные участки изотерм реального вещества АВ и СD (рис.1). Пусть Р ₁= Р; Р ₂= Р + dР; Т ₁= Т; Т ₂= Т + dТ. Выполненная за цикл работа δ А равна площади этого цикла на P – V диаграмме, а сам цикл, учитывая близость изотерм его образующих, можно приближенно считать параллелограммом.

Тогда

. (2.4)

В ходе изотермического фазового перехода (участок АВ) вещество получает от нагревателя количество теплоты, равное молярной теплоте перехода . Поэтому КПД цикла можно записать в виде

. (2.5)

Поскольку рассматривается цикл Карно, КПД этого цикла можно записать, используя теорему Карно:

. (2.6)

Приравняв выражение (2.5) и (2.6), получим

. (2.7)

Соотношение (2.7) называется уравнением Клапейрона-Клаузиуса. Его можно использовать для определения теплоты парообразования жидкости. Учитывая, что при температурах, далеких от критической, , получаем

. (2.8)

На участках невысоких давлений к пару можно применить законы идеального газа, и тогда удельный объем 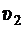можно определить из уравнения Клапейрона-Менделеева:

. (2.9)

Подставляя значение 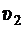из формулы (2.9) в соотношение (2.8), получим

. (2.10)

Считая величину q постоянной для исследуемого интервала изменения температуры, проинтегрируем уравнение (2.10)

. (2.11)

Полученная формула устанавливает связь между молярной теплотой парообразования воды, давлением и температурой водяного пара. Изменяя температуру пара T, необходимо построить график зависимости , по угловому коэффициенту которого можно определить молярную теплоту парообразования воды.

Постоянную интегрирования можно найти, если известно давление насыщенного пара P ₀ при какой – либо одной температуре T ₀. При этой температуре

(2.12)

Исключая постоянную интегрирования, получим

(2.13)

Соотношение (2.13) выражает зависимость давления насыщенного пара от температуры.

Не нашли, что искали? Воспользуйтесь поиском: