
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ ИДЕАЛЬНЫХ ГАЗОВ
1.1. Термодинамические параметры. @
Мысленно выделенная макроскопическая система, рассматриваемая методами термодинамики, называется термодинамической системой. Все тела, не включенные в состав исследуемой системы, называются внешней средой. Состояние системы задается термодинамическими параметрами (или, по-другому, параметрами состояния) – совокупностью физических величин, характеризующих свойства системы. Обычно в качестве основных параметров выбирают давление р, температуру Т и удельный объем v. Различают два типа термодинамических параметров: экстенсивные и интенсивные. Экстенсивные параметры пропорциональны количеству вещества в системе, а интенсивные не зависят от количества вещества и массы системы. Интенсивными параметрами являются давление, температура, удельный объем и др., а экстенсивными – объем, энергия, энтропия.
Объем пропорционален количеству вещества в системе. При расчетах удобнее оперировать с удельным объемом v – это величина, равная отношению объема к массе системы, то есть объем единицы массы v = V/m = 1/ρ, где ρ – плотность вещества.
Давлением называется физическая величина  где dFn- проекция силы на нормаль к поверхности площадью dS.
где dFn- проекция силы на нормаль к поверхности площадью dS.
Температура – это физическая величина, характеризующая энергию макроскопической системы, находящейся в состоянии термодинамического равновесия. Температура системы является мерой интенсивности теплового движения и взаимодействия частиц, образующих систему. В этом состоит молекулярно-кинетический смысл температуры. В настоящее время существует две температурных шкалы – термодинамическая (градуированная в Кельвинах (К)) и Международная практическая (градуированная в градусах Цельсия (˚С)). 1˚С = 1К. Связь между термодинамической температурой Т и температурой по Международной практической шкале имеет вид: Т = t + 273,15˚С.
Всякое изменение состояния термодинамической системы, характеризующееся изменением ее параметров, называется термодинамическим процессом. Термодинамический процесс называется равновесным, если при этом система проходит ряд бесконечно близких равновесных состояний. Равновесное состояние – это такое состояние, в которое система приходит в конце концов при неизменных внешних условиях и дальше остается в этом состоянии сколь угодно долго. Реальный процесс изменения состояния системы будет тем ближе к равновесному, чем медленнее он совершается.
1. 2. Уравнение состояния идеального газа. @
В молекулярно-кинетической теории широко используется физическая модель идеального газа. Это вещество, находящееся в газообразном состоянии, для которого выполняются следующие условия:
1. Собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда.
2. Между молекулами газа отсутствуют взаимодействия, кроме случайных столкновений.
3. Столкновения молекул газа между собой и со стенками сосуда абсолютно упругие.
Модель идеального газа можно использовать при изучении реальных газов, т.к. они при условиях, близких к нормальным (давление р0 = 1,013∙105Па, температура Т0=273,15К) ведут себя аналогично идеальному газу. Например, воздух при Т=230К и р= р0/50 по всем трем критериям подобен модели идеального газа.
Поведение идеальных газов описывается рядом законов.
Закон Авогадро: моли любых газов при одинаковых температуре и давлении занимают одинаковые объемы. При нормальных условиях этот объем равен VM=22,4∙10-3м3/моль. В одном моле различных веществ содержится одно и то же число молекул, называемое числом Авогадро NA= 6,022∙1023моль-1.
Закон Бойля – Мариотта: для данной массы газа при постоянной температуре произведение давления газа на его объем есть величина постоянная pV = const при Т = const и m = const.
Закон Шарля: давление данной массы газа при постоянном объеме изменяется линейно с температурой р=р0(1+αt) при V = const и m = const.
Закон Гей-Люссака: объем данной массы газа при постоянном давлении изменяется линейно с температурой V = V0(1+αt) при р = const и m = const. В этих уравнениях t – температура по шкале Цельсия, р0 и V0 -давление и объем при 0°С, коэффициент α =1/273,15 К-1.
Французский физик и инженер Б.Клапейрон и русский ученый Д.И.Менделеев, объединив закон Авогадро и законы идеальных газов Бойля – Мариотта, Шарля и Гей – Люссака, вывели уравнение состояния идеального газа – уравнение, связывающее вместе все три термодинамических параметра системы: для одного моля газа рVМ= RT и для произвольной массы газа
 |
где VМ – молярный объем, т.е. объем одного моля газа, R – молярная газовая постоянная, равная 8,31Дж/(моль·К), М – молярная масса, V= VМ· m/M – объем всей массы газа, n = m/M – количество вещества в молях. Это уравнение называется уравнением Менделеева– Клапейрона.
Существует еще одна форма записи данного уравнения:
 |
Ее можно получить, если учесть, что k =R/NA = 1,38∙10-23 Дж/К – это постоянная Больцмана, а n =NA/VМ – это концентрация молекул газа.
Для расчета давления в смеси разных газов применяется закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений входящих в нее газов: р =р1 + р2 + … + pn. Парциальное давление – это такое давление, которое производил бы газ, входящий в состав газовой смеси, если бы он один занимал объем, равный объему смеси при той же температуре. Для расчета парциального давления идеального газа используют уравнение Менделеева– Клапейрона.
1. 3. Основное уравнение молекулярно – кинетической теории идеальных газов и его следствия. @
Рассмотрим одноатомный идеальный газ, занимающий некоторый объем V (рис.1.1.) Пусть число столкновений между молекулами пренебрежимо мало по сравнению с числом столкновений со стенками сосуда.  Выделим на стенке сосуда некоторую элементарную площадку ΔS и вычислим давление, оказываемое на эту площадку. При каждом соударении молекула, массой m0, движущаяся перпендикулярно площадке со скоростью υ, передает ей импульс, который представляет собой разницу импульсов молекулы до и после соударения:
Выделим на стенке сосуда некоторую элементарную площадку ΔS и вычислим давление, оказываемое на эту площадку. При каждом соударении молекула, массой m0, движущаяся перпендикулярно площадке со скоростью υ, передает ей импульс, который представляет собой разницу импульсов молекулы до и после соударения:
m0υ -(-m0υ) = 2m0υ.
За время Δt площадки ΔS достигнут только те молекулы, которые заключены в объеме цилиндра с основанием ΔS и длиной υΔt. Это число молекул будет nυΔSΔt, где n – концентрация молекул. Необходимо, однако, учитывать, что реально молекулы движутся к площадке под разными углами и имеют различные скорости, причем скорость молекул при каждом соударении меняется. Для упрощения расчетов хаотическое движение молекул заменяют движением вдоль трех взаимно перпендикулярных координатных осей, так что в любой момент времени вдоль каждого из них движется 1/3 молекул, причем половина – 1/6 – движется в одну сторону, половина – в противоположную. Тогда число ударов молекул, движущихся в заданном направлении, о площадку ΔS будет nυΔSΔt /6. При столкновении с площадкой эти молекулы передадут ей импульс
 .
.
В данном случае, когда сила, действующая на единицу площади, постоянна, для давления газа на стенку сосуда мы можем записать р = F/ΔS = ΔP/ΔSΔt = = nm0υ2/3. Молекулы в сосуде движутся с самыми различными скоростями υ1,υ2….υn, общее число их – N. Поэтому необходимо рассматривать среднюю квадратичную скорость, которая характеризует всю совокупность молекул:
 |
Таким образом, давление газа, оказываемое им на стенку сосуда, будет равно
 |
Приведенное выше уравнение и есть основное уравнение молекулярно-кинетической теории идеальных газов. Поскольку m0‹υкв›2/2 – это средняя энергия поступательного движения молекулы ‹ εпост›, уравнение можно переписать в виде:
 |
Следствия:
1. Учитывая, что концентрация n = N/V, получаем
 |
где E – суммарная кинетическая энергия поступательного движения всех молекул газа. Таким образом, давление равно двум третям энергии поступательного движения молекул, содержащихся в единице объема газа.
 |
2. Для вывода второго следствия воспользуемся первым следствием и уравнением Менделеева-Клапейрона:
Энергия молекул Е в веществе пропорциональна количеству вещества в системе и температуре.
4.
 |
Найдем еще кинетическую энергию поступательного движения одной молекулы ‹ εпост›, учитывая
k =R/NA получим:
 |
Отсюда следует, что средняя кинетическая энергия хаотического поступательного движения молекул идеального газа пропорциональна его абсолютной температуре и зависит только от нее, т.е. температура есть количественная мера энергии теплового движения молекул. При одинаковой температуре средние кинетические энергии молекул любого газа одинаковы. При Т=0К ‹εпост› = 0 и поступательное движение молекул газа прекращается, однако анализ различных процессов показывает, что Т = 0К – недостижимая температура.
4. Учитывая, что ‹εпост› = 3kT/2, р = 2n‹ εпост›/3, получим отсюда: р = nkT.
Мы получили уже знакомый нам вариант уравнения Менделеева-Клапейрона, выведенный в данном случае из понятий молекулярно-кинетической теории статистическим методом. Последнее уравнение означает, что при одинаковых температуре и давлении все газы содержат в единице объема одинаковое число молекул.
1. 4. Барометрическая формула. @
При выводе основного уравнения молекулярно-кинетической теории предполагалось, что если на молекулы газа не действуют внешние силы, то молекулы равномерно распределены по объему. Однако молекулы любого газа находятся в потенциальном поле тяготения Земли. Тяготение, с одной стороны, и тепловое движение молекул, с другой, приводят к некоторому стационарному состоянию газа, при котором концентрация молекул газа и его давление с высотой убывают. Выведем закон изменения давления газа с высотой, предполагая при этом, что поле тяготения однородно, температура постоянна и масса всех молекул одинакова. Если атмосферное давление на высоте h равно р, то на высоте h+dh оно равно р + dp (рис.1.2). При dh > 0, dр < 0, т.к. давление с высотой убывает. Разность давлений р и (р + dр) равна гидростатическому давлению столба газа авсd, заключенного в объеме цилиндра высотой dh и площадью с основанием равным единице. Это  запишется в следующем виде: p- (p+dp) = gρdh, - dp = gρdh или dp = ‑gρdh, где ρ – плотность газа на высоте h. Воспользуемся уравнением состояния идеального газа рV = mRT/M и выразим плотность ρ=m/V=pM/RT. Подставим это выражение в формулу для dр:
запишется в следующем виде: p- (p+dp) = gρdh, - dp = gρdh или dp = ‑gρdh, где ρ – плотность газа на высоте h. Воспользуемся уравнением состояния идеального газа рV = mRT/M и выразим плотность ρ=m/V=pM/RT. Подставим это выражение в формулу для dр:
dp = - pMgdh/RT или dp/p = - Mgdh/RT
Интегрирование данного уравнения дает следующий результат:  Здесь С – константа и в данном случае удобно обозначить постоянную интегрирования через lnC. Потенцируя полученное выражение, находим, что
Здесь С – константа и в данном случае удобно обозначить постоянную интегрирования через lnC. Потенцируя полученное выражение, находим, что
 |

При условии h=0 получим, что С=р0, где р0-давление на высоте h=0.
 |
Данное выражение называется барометрической формулой. Она позволяет найти атмосферное давление в зависимости от высоты, или высоту, если известно давление.
Зависимость давления от высоты демонстрирует рисунок 1.3. Прибор для определения высоты над уровнем моря называется высотомером или альтиметром. Он представляет собой барометр, проградуированный в значениях высоты.
1. 5. Закон Больцмана о распределении частиц во внешнем потенциальном поле. @
 |
Если воспользоваться выражением р = nkT, то можно привести барометрическую формулу к виду:
 |
здесь n – концентрация молекул на высоте h, n0 – то же у поверхности Земли. Так как М = m0NA, где m0 – масса одной молекулы, а R = k NA, то мы получим П = m0gh – это потенциальная энергия одной молекулы в поле тяготения. Поскольку kT~‹εпост›, то концентрация молекул на определенной высоте зависит от соотношения П и ‹εпост›
Полученное выражение называется распределением Больцмана для внешнего потенциального поля. Из него следует, что при постоянной температуре плотность газа (с которой связана концентрация) больше там, где меньше потенциальная энергия его молекул.
1. 6. Распределение Максвелла молекул идеального газа по скоростям. @
При выводе основного уравнения молекулярно-кинетической теории отмечалось, что молекулы имеют различные скорости. В результате многократных соударений скорость каждой молекулы меняется со временем по модулю и по направлению. Из-за хаотичности теплового движения молекул все направления являются равновероятными, а средняя квадратичная скорость остается постоянной. Мы можем записать
 |
Постоянство ‹υкв› объясняется тем, что в газе устанавливается стационарное, не меняющееся со временем распределение молекул по скоростям, которое подчиняется определенному статистическому закону. Этот закон теоретически был выведен Д.К.Максвеллом. Он рассчитал функцию f(u), называемую функцией распределения молекул по скоростям. Если разбить диапазон всех возможных скоростей молекул на малые интервалы, равные du, то на каждый интервал скорости будет приходиться некоторое число молекул dN(u), имеющих скорость, заключенную в этом интервале (Рис.1.4.).

Функция f(v) определяет относительное число молекул, скорости которых лежат в интервале от u до u+ du. Это число - dN(u)/N= f(u)du. Применяя методы теории вероятностей, Максвелл нашел вид для функции f(u)

 Данное выражение - это закон о распределении молекул идеального газа по скоростям. Конкретный вид функции зависит от рода газа, массы его молекул и температуры (рис.1.5). Функция f(u)=0 при u=0 и достигает максимума при некотором значении uв, а затем асимптотически стремится к нулю. Кривая несимметрична относительно максимума. Относительное число молекул dN(u)/N, скорости которых лежат в интервале du и равное f(u)du, находится как площадь заштрихованной полоски основанием dv и высотой f(u), показанной на рис.1.4. Вся площадь, ограниченная кривой f(u) и осью абсцисс равна единице, потому что, если просуммировать все доли молекул, имеющих всевозможные значения скорости, то получается единица. Как показано на рис.1.5, с ростом температуры кривая распределения смещается вправо, т.е. растет число быстрых молекул, но площадь под кривой остается постоянной, т.к. N = const.
Данное выражение - это закон о распределении молекул идеального газа по скоростям. Конкретный вид функции зависит от рода газа, массы его молекул и температуры (рис.1.5). Функция f(u)=0 при u=0 и достигает максимума при некотором значении uв, а затем асимптотически стремится к нулю. Кривая несимметрична относительно максимума. Относительное число молекул dN(u)/N, скорости которых лежат в интервале du и равное f(u)du, находится как площадь заштрихованной полоски основанием dv и высотой f(u), показанной на рис.1.4. Вся площадь, ограниченная кривой f(u) и осью абсцисс равна единице, потому что, если просуммировать все доли молекул, имеющих всевозможные значения скорости, то получается единица. Как показано на рис.1.5, с ростом температуры кривая распределения смещается вправо, т.е. растет число быстрых молекул, но площадь под кривой остается постоянной, т.к. N = const.
Скорость uв, при которой функция f(u) достигает максимума, называется наиболее вероятной скоростью. Из условия равенства нулю первой производной функции f(v) ′ = 0 следует, что
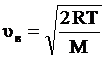 |
На рисунке 1.4. отмечена еще одна характеристика – средняя арифметическая скорость молекулы. Она определяется по формуле:
 |
 Опыт, проведенный немецким физиком О.Штерном, экспериментально подтвердил справедливость распределения Максвелла (рисунок 1.5.). Прибор Штерна состоит из двух коаксиальных цилиндров. Вдоль оси внутреннего цилиндра со щелью проходит платиновая проволока, покрытая слоем серебра. Если пропустить по проволоке ток,она нагревается и серебро испаряется. Атомы серебра, вылетая через щель, попадают на внутреннюю поверхность второго цилиндра. Если прибор будет вращаться, то атомы серебра осядут не против щели, а сместятся от точки О на некоторое расстояние. Исследование количество осадка позволяет оценить распределение молекул по скоростям. Оказалось, что распределение соответствует максвелловскому.
Опыт, проведенный немецким физиком О.Штерном, экспериментально подтвердил справедливость распределения Максвелла (рисунок 1.5.). Прибор Штерна состоит из двух коаксиальных цилиндров. Вдоль оси внутреннего цилиндра со щелью проходит платиновая проволока, покрытая слоем серебра. Если пропустить по проволоке ток,она нагревается и серебро испаряется. Атомы серебра, вылетая через щель, попадают на внутреннюю поверхность второго цилиндра. Если прибор будет вращаться, то атомы серебра осядут не против щели, а сместятся от точки О на некоторое расстояние. Исследование количество осадка позволяет оценить распределение молекул по скоростям. Оказалось, что распределение соответствует максвелловскому.
Не нашли, что искали? Воспользуйтесь поиском: