
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Указания к графической части
4.1. Построение отдельных термодинамических процессов и цикла в координатах P-V
4.1.1. Определив основные параметры в характерных точках цикла, можно приступать к построению отдельных процессов цикла в координатах P-V.
4.1.2. Перед тем, как начать построение процессов цикла необходимо выбрать масштабы давлений mp, бар/мм и удельных объемов mv, м³/(кг·мм).
Эти масштабы следует принять такими, чтобы получить высоту диаграммы, равной 1,5…1,8 ее основания.
4.1.3. Построение изохорного и изобарного процессов в координатах P-V не представляет особого труда – они будут представлены прямыми.
Сжатие или расширение рабочего тела в идеальных газовых циклах происходит, как правило, по адиабате.
4.1.4. Рассмотрим графическое построение этого процесса в координатах P и V (рис. 1).
В принятом масштабе на график наносятся параметры одной из точек процесса. Построение удобнее начинать с точки, соответствующей минимальному объему т.е. с начала расширения или с конца сжатия. Из начала координат проводится луч под произвольным углом α к оси абсцисс (этот угол рекомендуется принимать таким, чтобы тангенс угла его равнялся 0,3). К оси координат из начала координат проводится луч под углом β связанным с углом α зависимостью:
tg β = (1 + tg α)к – 1,
где к - показатель адиабаты сжатия и расширения.
 |
Из точки, соответствующей концу сжатия или началу расширения (например, точки 2) проводятся две линии: одна - параллельно оси абсцисс до встречи с осью ординат, другая - параллельно оси ординат до встречи с лучом, проведенным к оси абсцисс. Из точки пересечения с осью ординат первой линии под углом 45° к оси ординат проводится линия до встречи с лучом, проведенным под углом b. Из полученной точки проводится горизонтальная прямая. Из точки пересечения второй прямой с лучом, проведенным под углом a, проводится прямая под углом 45° к оси абсцисс до встречи с ней, и из этой точки проводится вертикальная прямая до пересечения с ранее проведенной горизонтальной прямой. Эта точка лежит на адиабате сжатия. Из точки пересечения горизонтальной прямой с осью ординат вновь проводим прямую под углом 45° до пересечения с лучом, проведенным под углом b. Из точки пересечения проводим горизонтальную прямую до встречи с ординатой, проведенной с точки А и т.д.
4.1.5. Аналогичным образом строится и адиабата расширения. Построение адиабат сжатия и расширения может быть выполнено также аналитическим способом, с использованием уравнения адиабаты.
4.1.6. Для каждого из построенных процессов определяется графически величина внешней L и располагаемой L 0 работы, а для процессов сжатия и расширения - показатель адиабаты.
4.1.7. Определение работ L и L 0 рассмотрим на примере адиабатного процесса 1¢-2¢. Точки 1 и 2 начала и конца процесса проектируем на ось координат; проекции их обозначаем: 1 и 2 на оси абсцисс и 1¢¢ и 2¢¢ на оси ординат.
4.1.8. Внешняя работа выражается площадью фигуры, ограниченной осью абсцисс, крайними ординатами и кривой процесса т.е.
L = пл.(1-2-2′-1′).
4.1.9. Располагаемая работа выражается площадью, ограниченной осью ординат, крайними абсциссами и кривой процесса т.е.
L 0 = пл.(1-2-2′′-1′′).
4.1.10. После построения отдельных процессов в координатах строится цикл путем переноса на график кривых каждого из процессов, составляющих цикл. Площадь замкнутой фигуры, ограниченной кривыми цикла, выражает работу газов за цикл.
L ц = пл.(1-2-3-4).
4.2. Построение отдельных термодинамических процессов и цикла в координатах T-S
4.2.1. Наряду с аналитическими методами решения задач по термодинамическим процессам широко применяются графические методы. Наиболее распространенным из них является метод, основанный на использовании T-S диаграммы.
4.2.2. Метод графического решения задач рассмотрим на конкретном примере, приняв в качестве составляющих термодинамические процессы, составляющие цикл. При этом следует помнить, что диаграмма T-S строится по рассчитанным параметрам основных точек цикла.
Обычно при решении задач по термодинамическим процессам не требуется определять абсолютное значение энтропии для какого-либо состояния; достаточно определить только изменение энтропии в процессе; поэтому начало отсчета энтропии выбирают условно.
а) Адиабатный процесс сжатия 1-2 (рисунок 2)
 |
4.2.3 Адиабатный процесс в координатах T-S изображается вертикальной прямой. Эта прямая проводится между точками 1 и 2, которые находятся по значениям температур Т 1 и Т 2.
Построив адиабату 1-2 приступаем к построению изобары и изохоры в заданном для адиабаты интервале температур.
Для этого из точки 1, отложив значения ΔSp=  ·ln(T1/T2) и в сторону возрастания энтропии ΔSv=
·ln(T1/T2) и в сторону возрастания энтропии ΔSv=  ·ln(T1/T2) определяем положение точек 2 p и 2 v.
·ln(T1/T2) определяем положение точек 2 p и 2 v.
Промежуточные точки кривых наносятся на график по значениям изменений энтропии ΔS, которые определяются из выражений:
Δ S′p=  ·ln(T2/T′1) иΔ S′v=
·ln(T2/T′1) иΔ S′v=  ·ln(T2/T′1),
·ln(T2/T′1),
где T′1 – температура в промежуточной точке; Δ S′p иΔ S′v - изменение энтропии в точке 2 относительно значений энтропии в точке 1.
4.2.4. Для построения указанных кривых достаточно нанести на график две-три промежуточные точки. Из точки 1 опустим вниз ординату. Полученная площадь, заключенная между кривой изохорного процесса, крайними ординатами и осью абсцисс с учетом масштабов численно равна изменению внутренней энергии в процессе-2. Действительно
Δ U = U2 – U1 = пл .(2v-2v′-1′-1)·mT·ms.
Здесь mT – масштаб температуры, ms – масштаб энтропии.
Площадь под изобарой 1-2p численно равна изменению энтальпии в процессе 1-2, т.е.
Δ i = i2 – i1 = пл .(2p-2p′-1′-1)·mT ·ms
4.2.5. Адиабатный процесс происходит без теплообмена с окружающей средой, т.е. dq = 0
б) Изохорный процесс 2-3 (рисунок 3)
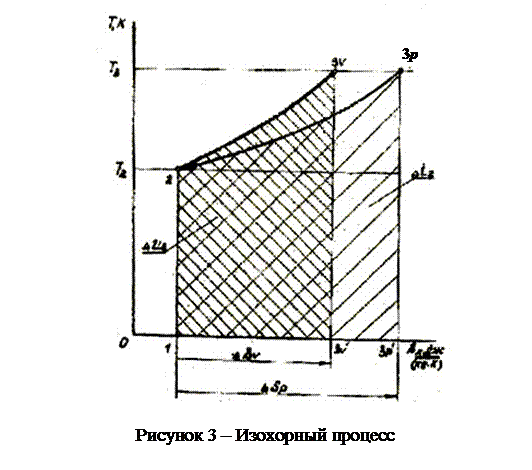 |
4.2.6. Площадь под изохорой численно равна количеству подведенного тепла, знак которого определяется из выражения:
dq = T·ds
Так как абсолютная температура всегда положительна, то знак dq определяется значением ds. В процессе 2-3 энтропия увеличивается, значит ds имеет знак плюс, следовательно, и dq так же имеет знак плюс.
4.2.7. Тепло процесса 2-3 равно
q2-3 = пл .(1-2-3v-3v′)·mT·ms
4.2.8. Изменение внутренней энергии в изохорном процессе равно количеству подведенного тепла Δ U = q.
4.2.9. Для определения изменения энтальпии из точки 2 проводим изобару 2-3 p до пересечения с изотермой Т 3.
Для этого определяем изменение энтропии для изобарного процесса в том же интервале температур (от Т2 до Т3).
Δ Sp =  · ln(T3/T2)
· ln(T3/T2)
Площадь под изобарой 2-3p выражает изменение энтальпии в изохорном процессе 2-3.
в) Адиабатный процесс расширения 3-4 (рисунок 4)
Адиабатный процесс расширения строится аналогично процессу сжатия с учетом знака изменения энтропии.
г) Изобарный процесс 4-1 (рисунок 5)
4.2.10 Площадь под изобарой 4-1з численно равна количеству подведенного тепла (изменению энтальпии в процессе 4-1)
qp = Δ i = пл .(1p-4-4′-1′)·mT ·ms.
Площадь под изохорой 4-1 v, проведенной из точки 4 до пересечения с изотермой T1, численно равна изменению внутренней энергии в процессе 4-1 v, т.е. qv = Δ U = пл .(1v-4-4′-1v′).
Для построения изохоры пользуются уравнением:
Δ Sv =  ln(T1/T4), кДж/(кг·К).
ln(T1/T4), кДж/(кг·К).
4.3. Построение цикла в координатах T-S
4.3.1. После построения отдельных процессов в координатах T-S строится цикл путем переноса на график кривых каждого из процессов, составляющих цикл (рис. 6). На рис. 8 изображен цикл ДВС со смешанным подводом тепла.
4.3.2. Площадь замкнутой фигуры, ограниченной кривыми цикла, выражает количество тепла, преобразованного в механическую работу:
 q о = пл.(1-2-3-4).
q о = пл.(1-2-3-4).
4.3.3. Площадь, ограниченная верхней кривой цикла, осью абсцисс, крайними ординатами, выражает количество подведенного тепла в цикле:
q 1 = пл.(2-3-1-1).
4.3.4. Отношение этих площадей равно термическому коэффициенту полезного действия цикла:
ηt = (1-2-3-4) / (2-3-1-1).
Общая компоновка графиков, оформление и их взаимное размещение приведены на рисунках 7, 9, 10, 11.

Рисунок 6 – Схема ГТУ: 1 – компрессор; 2 – камера сгорания; 3 – сопловой
аппарат; 4 – рабочие лопатки турбины

Рисунок 7 – Цикл ГТУ с изобарным подводом теплоты:
а – в P-V координатах; б – в T-S координатах

Рисунок 8 – Схема устройства и диаграмма рабочего процесса четырехтактного дизельного ДВС: 1 – рабочий цилиндр; 2 – впускной клапан; 3 – форсунка; 4 – выпускной клапан; 5 – поршень; 6 – шатун; 7 – кривошип; 8 - коленвал

Рисунок 9 – Цикл ДВС с изохорным подводом теплоты:
а – в P-V координатах; б – в T-S координатах

Рисунок 10 – Цикл ДВС с изобарным подводом теплоты:
а – в P-V координатах; б – в T-S координатах

Рисунок 11 – Цикл ДВС со смешанным подводом теплоты:
а – в P-V координатах; б – в T-S координатах
Не нашли, что искали? Воспользуйтесь поиском: