
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Ответ: прочность обеспечена.
Решение
2. Определяем площадь сечения с учетом ослабления
Ainf = b·h - b·d = 0,1·0,125 – 0,1·0,016 = 0,0109 м2.
3. Проверяем прочность деревянной подвески по формуле

Условие не выполняется. Прочность не обеспечена..
Задача №6: Проверить прочность деревянной балки сечением b×h=175×250 мм из сосны 1 сорта, если расчетная нагрузка составила g =2,4 кН/м. Расчетный пролет балки l=4,2 м. Расчетное сопротивление древесины на изгиб вдоль волокон fm,d= 16 Мпа, kmod =0,80 (2 класс эксплуатации). Указать расчетную схему элемента, эпюры расчетных усилий.

1. Изображаем расчетную схему балки, эпюры поперечной силы и изгибающих моментов.
Определяем максимальную поперечную силу
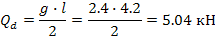
Определяем максимальный изгибающий момент
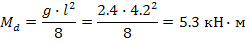
Определяем момент сопротивления сечения
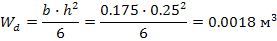
2.Проверяем прочность сечения балки на изгиб
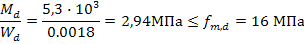
2.94мПа<16*0,80=12,8Мпа
Условие выполняется
Задача №7: Проверить прочность центрально-растянутой деревянной подвески сечением b×h=100×130 мм, ослабленной отверстием для болтов d=16 мм. Расчетная растягивающая сила Nd=100 кН. Расчетное сопротивление неклееной древесины 2 сорта на растяжение вдоль волокон ft,o,d=7 Мпа, kmod =0,80 (2 класс эксплуатации). Указать расчетную схему элемента.
,
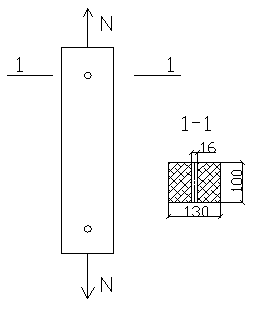
1. Определяем площадь сечения с учетом ослабления
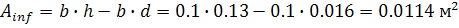
2. Проверяем прочность деревянной подвески по формуле
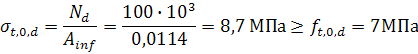
8,7Мпа>8,7*0,80=5,7мПа
Условие не выполняется
Ответ: прочность подвески не обеспечена.
Задача №8: Проверить прочность главной балки, выполненной из прокатного двутавра №40 при следующих данных:
- расчетный пролет 1 = 6 м;
- расчетная нагрузка q = 30,5 кН/м;
- расчетное сопротивление по пределу текучести Ry==240 МПа (для стали С255)
Изобразить расчетную схему элемента, эпюры расчетных усилий.

1. Изображаем расчетную схему балки, эпюры поперечной силы и изгибающих моментов.
Определяем максимальную поперечную силу

Определяем максимальный изгибающий момент

2. По таблице сортамента «Двутавровые балки» по ГОСТ 8239-72 двутавр №40 Wx=953 см3, Ix=19062 см4.
3. Проверяем прочность балки
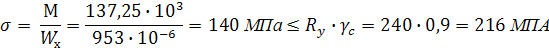
=240Мпа.
Прочность обеспечена
Задача №9: Проверить прочность и прогиб прокатной балки рабочей площадки из двутавра №20 стали марки С275. Нормативная нагрузка q" = 5 кН/м, расчетная нагрузка q = 9,5 кН/м, расчетный пролет 1 = 6,6 м, коэффициент условий работы ус = 1. Расчетное сопротивление по пределу текучести Ry==270 МПа (для стали С275). Модуль упругости стали Е=2,06*105Мпа.
Изобразить расчетную схему элемента, эпюры расчетных усилий.
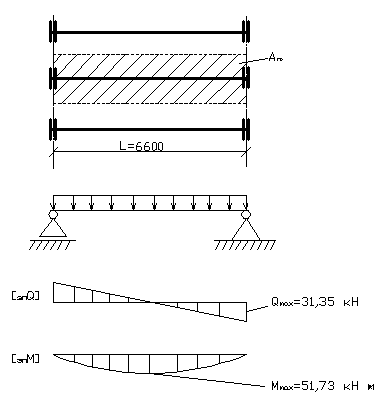
1. Изображаем расчетную схему балки, эпюры поперечной силы и изгибающих моментов.
Определяем максимальную поперечную силу
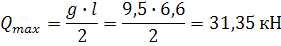
Определяем максимальный изгибающий момент
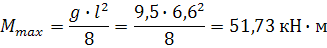
2. По таблице сортамента «Двутавровые балки» по ГОСТ 8239-72 для двутавра №20 Wx=184 см3, Ix=1840 см4, масса 1 м – 21 кг, t=8,4 мм.
3. Проверяем прочность балки
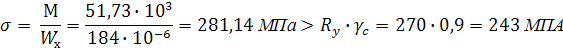
Прочность не обеспечена
4. Проверяем прогиб балки

Жесткость балки не обеспечена
Задача №10: Определить несущую способность N из условия прочности центрально-сжатого элемента стропильной фермы, изготовленного из швеллера №24 стали марки С245. Коэффициент условия работы γс=1, высота элемента Н=2.6 м. сопротивление по пределу текучести Ry==240 МПа (для стали С245). Закрепление концов элемента – шарнирное. Изобразить расчетную схему элемента.
1. По таблице сортамента «Двутавровые балки» для профиля №24 определяем площадь арматуры Аn=30,6см2.
2. Выражаем N из формулы прочности центрально-сжатых металлических элементов N /An≤Ry·  c
N= Ry· c
N= Ry·  c·An
N=240·106·1·30,6·10-4=734,4kH
Ответ: 734,4kH c·An
N=240·106·1·30,6·10-4=734,4kH
Ответ: 734,4kH
| 
|
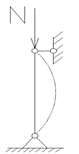
11. Определить несущую способность N из условия устойчивости центрально-сжатого элемента стропильной фермы, изготовленного из швеллера №24 стали марки С245. Коэффициент условия работы γс=1, высота элемента Н=2,6 м. Расчетное сопротивление по пределу текучести Ry==240 МПа (для стали С245). Закрепление концов элемента – шарнирное. Изобразить расчетную схему элемента.
1.По таблице сортамента «Швеллеры» для сечения №24 определяем площадь А=30,6 см2, ίх=9,73 см, ίу=2,6 см, t=10 мм. Минимальный радиус инерции ίmin= ίу=2,6 см
2.Для заданной расчетной схемы коэффициент μ=1,0, тогда расчетная длина элемента
lef=μ·l=1·2,6=2,6м
3.Гибкость элемента
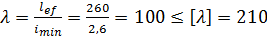 (таб. 19 СНиП ІІ-23-81), условие выполнено
(таб. 19 СНиП ІІ-23-81), условие выполнено
По 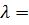 100 и Ry==240 МПа по таб. 72 СНиП ІІ-23-81 определяем коэффициент продольного изгиба φ=0,542
100 и Ry==240 МПа по таб. 72 СНиП ІІ-23-81 определяем коэффициент продольного изгиба φ=0,542
4.Определяем несущую способность из условия устойчивости
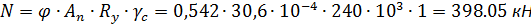
Задача №12: Проверить прочность сварного соединения встык листов шириной l=500 мм, толщиной t1=10 мм, t2=6 мм при действии расчетного осевого усилия растяжения N=600 кН. Материал – листовая сталь марки С275, коэффициент условий работы γс=0,95. Расчетное сопротивление стыкового шва при работе на растяжение при физическом контроле качества шва 
Сварка ручная с физическим контролем качества шва.
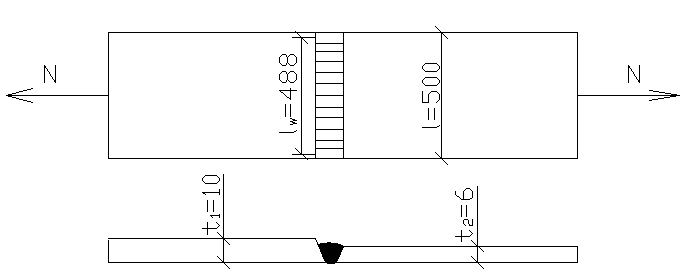
1. Определяем расчетную длину шва
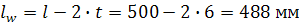
2. Поверяем прочность стыкового соединения
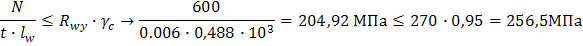
Ответ: прочность сварного стыкового шва обеспечена
Задача №13. Проверить прочность центрально-сжатого элемента стропильной фермы, выполненного из двутавра №12, стали марки С245, если коэффициент условий работы γс=1, высота элемента Н=1,97 м, расчетное усилие N=240 кН. Расчетное сопротивление по пределу текучести Ry=240 МПа (для стали С245). Изобразить расчетную схему элемента.
1.По таблице сортамента «Двутавровые балки» для профиля №12 определяем площадь арматуры Аn=14,76см2.
2. Проверяем прочность по формуле N/An≤Ry·  c
240·103/14.7·10-4 ≤ 240·106·1
163Мпа<240Мпа
Прочность обеспечена c
240·103/14.7·10-4 ≤ 240·106·1
163Мпа<240Мпа
Прочность обеспечена
| 
|
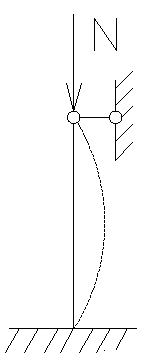
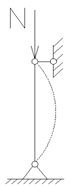
№14. Проверить устойчивость центрально-сжатого элемента стропильной фермы, выполненного из двутавра №20, стали марки С245, если коэффициент условий работы γс=1, высота элемента Н=2,07 м, расчетное усилие N=200 кН. Расчетное сопротивление по пределу текучести Ry=240 МПа (для стали С245). Закрепление концов элемента: сверху – шарнирное, снизу – жесткое. Изобразить расчетную схему элемента.
Решение:
1.По таблице сортамента «Двутавровые балки» для профиля №20 определяем площадь арматуры Аn=26,8см2
2. Определяем гибкость элемента  =Lef/imin
Lef= =Lef/imin
Lef=  *L=1*2,07=2,07м
3.Определяем коэффициент продольного изгиба по таблице 72 СНиП *L=1*2,07=2,07м
3.Определяем коэффициент продольного изгиба по таблице 72 СНиП
 =0,542
4.Проверяем устойчивость
N/An* =0,542
4.Проверяем устойчивость
N/An*  ≤Ry* ≤Ry*  c
200*103/26,8*10-4*0,542≤240*106*1
128Мпа<240Мпа
Устойчивость обеспечена c
200*103/26,8*10-4*0,542≤240*106*1
128Мпа<240Мпа
Устойчивость обеспечена
| 
|
Задача №15: Проверить прочность центрально-нагруженного столба сечением 51Х64 см, высотой Н=5,1 м. Столб выполнен из пустотелого силикатного камня марки М125, раствор марки М50. Расчётное усилие N=300 кН. Условия закрепления: оба конца – шарнирные. Изобразить расчётную схему элемента.
Решение: 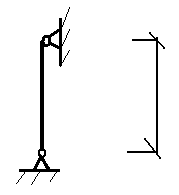
1. Определить площадь поперечного сечения столба.
A=b·h=0,51·0,64=0,3264м3 > 0,3м3
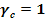
2. Определить упругую характеристику кладки из силикатного камня α=1000(табл. 15 СНиП)
3.Определить гибкость элемента
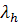 =
= 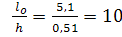
где  =1·5,1=5,1 м
=1·5,1=5,1 м
4. Определить по таб. 13 СНиП коэффициент продольного изгиба 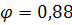
5.Т.к. h = 0,51, 
6.Определить расчётное сопротивление каменной кладки по таб. 2 СНиП R=1,7 МПа
7.Проверить прочность столба
N=300 кН < 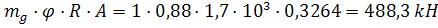
Ответ: прочность обеспечена.
№16. Проверить устойчивость центрально-нагруженного столба сечением 51Х64 см, высотой Н=5,1 м. Столб выполнен из пустотелого силикатного камня марки М125, раствор марки М50. Расчётное усилие N=250 кН. Условия закрепления: оба конца – шарнирные. Изобразить расчётную схему элемента.
A=b·h= 0,64 ·0,51=0,326м2 
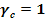
2.Определить упругую характеристику кладки из пустого силикатного кирпича α=1000 (таб. 15 СНиП)
3.Определить гибкость элемента
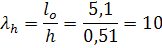
Где L0=1·5.1=5,1м. Определить по таб. 18. СНиП коэффициент продольного изгиба 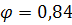 8. Т.к. h = 0,51, g w:val="EN-US"/></w:rPr><m:t>g</m:t></m:r></m:sub></m:sSub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Times New Roman"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>=1</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
8. Т.к. h = 0,51, g w:val="EN-US"/></w:rPr><m:t>g</m:t></m:r></m:sub></m:sSub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Times New Roman"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>=1</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
6. Определить расчётное сопротивление каменной кладки по таб. 2. СНиП. R=1, МПа
7. Определить несущую способность N
N=mg· 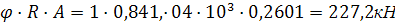 1∙0,88∙1,7∙103 ∙0,326=488кн
1∙0,88∙1,7∙103 ∙0,326=488кн
250КН<488КН
Вывод: несущая способность из условия устойчивости обеспечена.
Задача №17: Определить несущую способность N из условия прочности центрально-нагруженного столба сечением 51x51 см, выполненного из полнотелого силикатного кирпича марки М75 на растворе марки М50. Условия закрепления: верхний конец элемента свободен, нижний – жёстко защемлён. Высота столба Н=2,55 м. Изобразить расчётную схему элемента.
Решение: 
1.Определить площадь сечения столба
A=b·h= 0,51 ·0,51=0,2601м2 

2. Определить расчётное сопротивление каменной кладки по таб. 2. СНиП. С учётом коэффициента условий работы 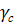
R= Rтаб ·  =1,3·0,8=1,04 МПа
=1,3·0,8=1,04 МПа
7. Определить несущую способность N
N=R·A=1,04·103·0,2601=270кН
Ответ: N=270 кН
Задача 18. Определить несущую способность N из условия устойчивости центрально-нагруженного столба сечением 38x51 см, выполненного из полнотелого силикатного кирпича марки М75 на растворе марки М50. Условия закрепления: верхний конец элемента свободен, нижний – жёстко защемлён. Высота столба Н=2,6 м. Изобразить расчётную схему элемента1.Определить площадь сечения столба
A=b·h= 0,38 ·0,51=0,1938м2 

2.Определить упругую характеристику кладки из пустого силикатного кирпича α=750 (таб. 15 СНиП)
3.Определить гибкость элемента
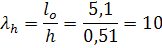
Где L0=2·2,6=5,2м. Определить по таб. 13. СНиП коэффициент продольного изгиба 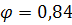
5. Т.к. h = 0,51, g w:val="EN-US"/></w:rPr><m:t>g</m:t></m:r></m:sub></m:sSub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Times New Roman"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>=1</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
6. Определить расчётное сопротивление каменной кладки по таб. 2. СНиП. С учётом коэффициента условий работы 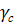
R= Rтаб ·  =1,3·0,8=1,04 МПа
=1,3·0,8=1,04 МПа
7. Определить несущую способность N
N=mg· 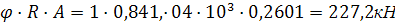
Ответ: N=227,2 кН
Задача №19: Определить требуемую марку камня силикатного пустотелого и марку раствора для центрально-сжатого столба двухпролётного промышленного здания. Расчётная схема- упругая верхняя опора и жесткое защемление в нижней опоре. Размеры сечения столба bxh=0,51x0,51 м, высота элемента Н=4,08 м. На столб действует расчётная продольная сила N=420 кН. Изобразить расчётную схему элемента.
Решение: 
1.Определяем площадь сечения столба
А=b 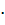 h=0,51
h=0,51 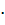 0,51=0,2601 м 2 ≤ 0,3 м 2
0,51=0,2601 м 2 ≤ 0,3 м 2
 = 0,8
= 0,8
2. Определяем упругую характеристику кладки из пустотелого силикатного камня α=1000(табл. 15 СНиП) для марки раствора 25-200
3.Определяем гибкость элемента
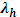 =
= 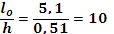
где 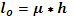 = 1,25
= 1,25 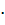 4,08=5,1 м
4,08=5,1 м
4. Определяем по таб. 13 СНиП коэффициент продольного изгиба 
5.Т.к. h=0,51, mg=1
6. Определяем требуемое расчётное сопротивление кладки
R треб= N/m g ·φ·A
R треб =  = 1,83 МПа =1834958 Па
= 1,83 МПа =1834958 Па
7. R таб = R треб / γc = 1,83/0,8=2,29 МПа
Определяем по таб. 2 СНиП марку кирпича и раствора
Ответ: марка кирпича 150, марка раствора 150; с R таб=2,4 МПа
Задача №20: Определить продольную растянутую арматуру железобетонной балки прямоугольного сечения с одинарным армированием, если максимальный изгибающий момент Msd = 30 кН-м, размеры сечения bxh = 0,15x0,30 м, величина с = 3,5 см. (коэффициент, а = 1).
сопротивление бетона осевому сжатию fcd= 10,67 МПа. Балка выполнена из бетона класса С16/20 Расчетное сопротивление ненапрягаемой арматуры fyd = 367 МПа(класс арматуры S400).
Изобразить поперечное сечение элемента, указать размеры и армирование.

Определяем рабочую высоту сечения
d=h-c = 0,3 - 0,035 = 0,265 м
Определяем предельное значение коэффициента
ξlim= ω / (1+ fyd/500 * (1- ω / 1.1)) = 0.765 / (1 + 367/500 * (1 – 0.765 / 1.1)) = 0.627

Определяем предельное значение коэффициента αlim
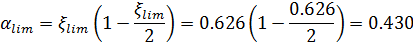
Определяем коэффициент αо
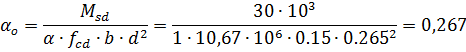
Проверяем условие αо≤ αlim→0,267≤ 0,430
Определяем по табл. 4 значение коэффициента ŋ:
Принимаем αо=0,269 и тогда ŋ=0,550
Определяем площадь растянутой арматуры
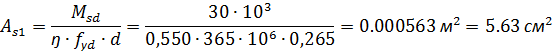
По сортаменту подбираем сечение арматуры равное:
- количество стержней – 1;
- диаметр арматуры 28 мм;
- площадь поперечного сечения – 3,801 см2
Задача №21. Определить предельный изгибающий момент Msd прямоугольного сечения с одинарным армированием, если размеры сечения bxh = 0,20x0,35 м, величина с =3,5,см. Балка армирована двумя стержнями Ø 20 мм. Расчетное сопротивление бетона осевому сжатию fcd=16,67 Мпа(бетон класса С25/30). Расчетное сопротивление ненапрягаемой арматуры fyd = 367МПа (класс арматуры S400). Коэффициент а = 1. Граничное значение относительно высоты сжатой зоны бетона ξlim=0.572. Изобразить поперечное сечение элемента, указать размеры и армирование.
.
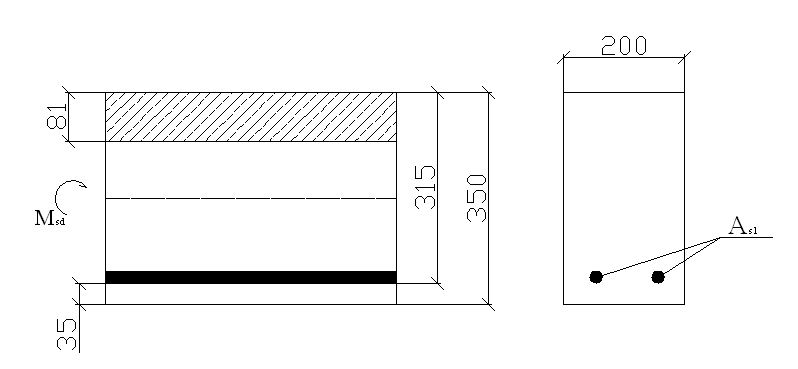
1. Определяем рабочую высоту сечения
d=h-c = 0,35 - 0,035 = 0,315 м
2. По сортаменту для 2-х стержней Ø 20 мм определяем площадь растянутой арматуры Аs1=6,28 см2
Определяем высоту сжатой зоны бетона
χeff = (fyd * As1) / (α * fcd * b) = (367*106 * 0.000628) / (1*16.67*106*0.20) = 0.069м
3. ξ = χeff / d = 0.068 / 0.315 = 0.215
4. Проверяем условие
ξ≤ ξlim→0,215≤0.572, условие выполняется
5. Определяем максимальный изгибающий момент:
Msd=fyd∙As1∙(d-0.5xeff)=367∙106∙6,28∙10-4(0,315-0,5∙0,069)=64,65кНм
относительно центра тяжести сжатого бетона:
Msd=b∙ а ∙ fcd ∙ xeff (d-0.5xeff)=0,2∙1∙16,6∙106∙0.069(0,315-0,5∙0,069)=64,26кНм
Ответ: Ммах=64,65кНм
№22. Выполнить сбор нормативных и расчетных нагрузок на 1 м2 покрытия скатной кровли (а = 25º) жилого дома в г. Гомеле следующего состава
- покрытие из асбестоцементных листов массой 1м2=15кг
- обрешетка из деревянных брусков 50*50мм, S=500мм, ρ = 500 кг/м3;
- стропильные ноги из бруса 75*200мм, S=1000мм, ρ = 500 кг/м3;
Вес снегового покрова для г. Гомеля S0 =0,8
Сбор нагрузок выполнить в табличной форме по образцу:
| Вид нагрузки и ее расчет | Нормативная нагрузка, кН/м2 | γf | Расчетная нагрузка, кН/м2 |
| |||
| покрытие из асбестоцементных листов массой 1м2=15кг | 15*10/103*0.9=0.135 | 1.35 | 0.18225 |
| - обрешетка из деревянных брусков 50*50мм, S=500мм, ρ = 500 кг/м3; | 0.05*0.05*500*10/103*0.9*0.5= =0.027 | 1.35 | 0.3645 |
| - стропильные ноги из бруса 75*200мм, S=1000мм, ρ = 500 кг/м3; | 0.075*0.2*500*10/103*0.9*0.5= 0.016 | 1.35 | 0.0216 |
| |||
| 21. снеговая | Sn=S0∙µ=0.8*1=0.8 | 1.6 | 1.28 |
| всего | 0,978 | 1,848 |
Задача №23: Проверить несущую способность железобетонной балки с одиночным армированием сечением bxh=15x30 см, с = 3,5 см. Расчетный изгибающий момент Msd = 56 кН·м, коэффициент а = 1. Сечение армировано 2 стержнями Ø12 мм. Расчетное сопротивление бетона осевому сжатию по формуле fcd= 13,33 МПа (класс бетона С20/25), расчетное сопротивление ненапрягаемой арматуры fyd = 367 МПа (класс арматуры S400).Изобразить поперечное сечение элемента, указать размеры и армирование.

1. Определяем рабочую высоту сечения
d=h-c = 0,30 - 0,035 = 0,265 м
2. По сортаменту для 2-х стержней Ø 12 мм определяем площадь растянутой арматуры Аs1=2,26 см2
Определяем высоту сжатой зоны бетона
χeff = (fyd * As1) / (α * fcd * b) = (367*106*0.000226) / (1*13.33*106*0.15) = 0.041 м
3. Определяем
ξ = χeff / d =0.048 / 0.265 = 0.181
4. Определяем предельное значение коэффициента
ξlim= ω / (1+ fyd/500 * (1- ω / 1.1)) = 0.743 / (1 + 367/500 * (1 - 0.743/1.1)) = 0.599
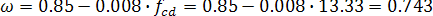
5. Проверяем условие
ξ≤ ξlim→0,181≤0.599, условие выполняется
6. Определяем максимальный изгибающий момент:
относительно центра тяжести растянутой арматуры
Мsd= fyd * As1(d-0,5 χeff)=367·103·2,26·10-4 (0.265-0.5·0.041)=
56 кН·м>20,3 Условие не выполняется
относительно центра тяжести сжатого бетона:

=·1·13,33·103·0,041 (0,265-0,5·0,041)=133.6 Кнм
56 кН·м <133.6 кН·м Условие выполняется
Задача №24: Проверить среднее давление на грунт под подошвой ленточного фундамента шириной b = 1,2 м жилого здания: если нагрузка на фундамент составит Nn = 120 кН, глубина заложения фундамента d = 1.4 м. Расчетное сопротивление грунта R=250 кПа, средний вес материала фундамента и грунта на его уступах уср=20 кН/м3. Изобразить расчетную схему ленточного фундамента здания без подвала, указать основные размеры и расчетные усилия
1. Определяем среднее давление под подошвой фундамента от действующей нагрузки
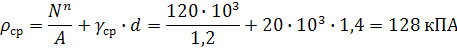
2. Проверяем условие ρср≤R→128≤250
Задача 25. Определить расчетное сопротивление грунта основания под фундамент здания без подвала при следующих исходных данных:
- вид грунта - песок мелкий;
- угол внутреннего трения φII = 20 град;
- коэффициенты Мy = 0,51; Мq = 3,06; Мc = 5,66
- ширина подошвы фундамента b = 2м;
- удельный вес грунта ниже подошвы фундамента γ' = 17,4 кН/м3;
- удельный вес грунта выше подошвы фундамента γ'' = 18 кН/м3;
- глубина заложения фундамента d1 = 1,2 м;
- расчетное значение удельного сцепления грунта под подошвой фундамента
сН = 17

26. Определить расчетное сопротивление грунта основания под фундамент здания с подвалом при следующих исходных данных:
- вид грунта - песок мелкий;
- угол внутреннего трения φII = 25 град;
- коэффициенты Мy = 0,78; Мq = 4,11; Мc = 6,76
- ширина подошвы фундамента b = 2,4 м;
- удельный вес грунта ниже подошвы фундамента γ' = 17кН/м3;
- удельный вес грунта выше подошвы фундамента γ'' = 17 кН/м3;
- коэффициенты γс2 = 1,10, γс1= 1,3, kz = 1, k = 1
- глубина заложения фундамента d1 = 1,2 м;
-глубина подвалаdb=2,0м
- расчетное значение удельного сцепления грунта под подошвой фундамента
сН = 17

1,3*1,1/1 (0,78*1*2,4+4,11*1,2*17+(4,11-1)2*17+6,76*17)=306,37кПа
| <== предыдущая лекция | | | следующая лекция ==> |
| Глава 27. Эпилог. ОБМАНУТАЯ НАДЕЖДА | | | Укажите достоинства и недостатки соединений на сварке, виды сварных соединений, типы сварных швов. Приведите формулы расчета стыковых и угловых швов. |
Не нашли, что искали? Воспользуйтесь поиском: